Угол между прямой и плоскостью — это одно из основных понятий в геометрии, а точнее в трехмерной геометрии. Для практического применения в различных областях, таких как инженерия, архитектура или графический дизайн, важно понять его определение и способы его вычисления.
Определение угла между прямой и плоскостью довольно простое. Представим, что есть прямая, заданная точкой на ней и направляющим вектором, а также плоскость, заданная точкой на ней и нормальным вектором. Углом между этой прямой и плоскостью является угол между направляющим вектором прямой и нормальным вектором плоскости.
Понимание этого определения важно для решения задач, связанных с геометрией пространства. Например, когда нужно вычислить угол между излучением света и поверхностью, чтобы правильно ориентировать и расположить источники света в помещении.
Существует несколько способов вычисления угла между прямой и плоскостью:
- Метод векторного произведения: используется для определения угла между векторами. Путем вычисления синуса угла между направляющим вектором прямой и нормальным вектором плоскости можно получить значение угла.
- Метод скалярного произведения: используется для нахождения угла между векторами. Поделив скалярное произведение направляющего вектора прямой и нормального вектора плоскости на произведение их длин, получаем косинус угла между ними.
- Альтернативно можно использовать теорему косинусов для вычисления угла между прямой и плоскостью. Это позволяет определить угол, исходя из длин сторон и противолежащего угла в треугольнике, образованном прямой и плоскостью.
Понимание и применение этих методов позволяют решать задачи, связанные с углом между прямой и плоскостью. Например, при расчете проекций объектов на плоскости, контроле положения и направления движения объектов в трехмерном пространстве или при создании трехмерной компьютерной графики.
Особенности определения угла между прямой и плоскостью: примеры
Одна из особенностей определения угла между прямой и плоскостью заключается в том, что угол может быть как острый, так и тупой, или даже прямым. Например, рассмотрим случай прямой, параллельной плоскости. В этом случае угол между прямой и плоскостью будет равен 0 градусов.
Еще одна особенность заключается в том, что угол между прямой и плоскостью может быть различным в разных точках прямой. Например, рассмотрим прямую, которая пересекает плоскость под углом. В этом случае угол между прямой и плоскостью будет разным в каждой точке пересечения.
Примеры использования угла между прямой и плоскостью возникают в различных областях, включая геометрию, физику и инженерию. Например, при построении трехмерных моделей, определении направления силы или определении направления луча света. Все эти примеры требуют понимания особенностей определения угла между прямой и плоскостью.
Определение угла между прямой и плоскостью
Для того чтобы определить угол между прямой и плоскостью, можно использовать следующий алгоритм:
- Найдите вектор, перпендикулярный плоскости. Если у вас есть уравнение плоскости в виде Ax + By + Cz + D = 0, то вектор нормали к плоскости будет (A, B, C).
- Найдите вектор направления прямой. Если у вас есть уравнение прямой в виде x = x0 + at, y = y0 + bt, z = z0 + ct, то вектор направления будет (a, b, c).
- Найдите скалярное произведение вектора направления прямой и вектора нормали плоскости. Формула для вычисления скалярного произведения двух векторов A и B: A · B = |A| |B| cos(θ), где θ — угол между векторами.
- Используя найденное скалярное произведение и формулу cos(θ) = A · B / (|A| |B|), вычислите значение угла θ.
- Если угол θ получился положительным, то он означает поворот вектора направления против часовой стрелки относительно вектора нормали плоскости. Если угол θ получился отрицательным, то он означает поворот вектора направления по часовой стрелке относительно вектора нормали плоскости.
Пример:
| Уравнение плоскости | 2x + 3y — z + 4 = 0 |
|---|---|
| Уравнение прямой | x = 1 + 2t, y = 2 — t, z = 3t |
| Вектор нормали плоскости | (2, 3, -1) |
| Вектор направления прямой | (2, -1, 3) |
| Скалярное произведение векторов | 2 * 2 + 3 * (-1) + (-1) * 3 = 1 |
| Значение угла | θ = acos(1 / (|2, 3, -1| * |2, -1, 3|)) ≈ 30.96° |
Таким образом, угол между прямой и плоскостью в данном примере составляет приблизительно 30.96 градусов.
Угол наклона прямой относительно плоскости
Когда угол наклона прямой относительно плоскости равен 90 градусам, прямая называется перпендикулярной плоскости. Это значит, что прямая пересекает плоскость под прямым углом и не лежит в плоскости.
Если угол наклона прямой относительно плоскости меньше 90 градусов, то прямая наклонена относительно плоскости в направлении, указанном углом. Направление определяется как внутрь плоскости (если угол острый), так и вовне плоскости (если угол тупой).
Если угол наклона прямой относительно плоскости больше 90 градусов, то прямая наклонена относительно плоскости в направлении, противоположном указанному углу. Направление определяется как внутрь плоскости (если угол острый), так и вовне плоскости (если угол тупой).
Примером угла наклона прямой относительно плоскости может служить ситуация, когда прямая проходит через горизонтальную плоскость под углом к ней. В этом случае угол наклона будет острый. А если прямая лежит на плоскости или совпадает с ней, то угол наклона будет равен 0 градусов.
Методы определения угла между прямой и плоскостью
Метод через векторы нормали
Один из наиболее распространенных методов определения угла между прямой и плоскостью основан на использовании векторов нормали плоскости и направляющего вектора прямой. Вектор нормали плоскости можно найти с помощью скалярного произведения двух других векторов, лежащих в плоскости. Затем, применив тригонометрические формулы, можно определить значение угла между прямой и плоскостью.
Метод через проекции
Еще одним способом определения угла между прямой и плоскостью является использование проекций. При этом методе необходимо проецировать направляющий вектор прямой на вектор нормали плоскости. Затем, найдя скалярное произведение проекций, можно определить значение угла между прямой и плоскостью.
Метод через уравнения плоскости и прямой
Еще один метод определения угла между прямой и плоскостью основан на использовании уравнений плоскости и прямой. Подставляя координаты точки принадлежащей прямой в уравнение плоскости и находя косинус угла между нормалью плоскости и направлением прямой, можно вычислить значение угла.
| Метод | Описание |
|---|---|
| Метод через векторы нормали | Определение угла с помощью векторов нормали плоскости и направляющего вектора прямой. |
| Метод через проекции | Определение угла с использованием проекций направляющего вектора прямой на вектор нормали плоскости. |
| Метод через уравнения плоскости и прямой | Определение угла с использованием уравнений плоскости и прямой. |
Выбор метода определения угла между прямой и плоскостью зависит от конкретной задачи и доступной информации о прямой и плоскости. Каждый из методов имеет свои преимущества и недостатки, и может быть удобным в различных ситуациях.
Примеры угла между прямой и плоскостью
-
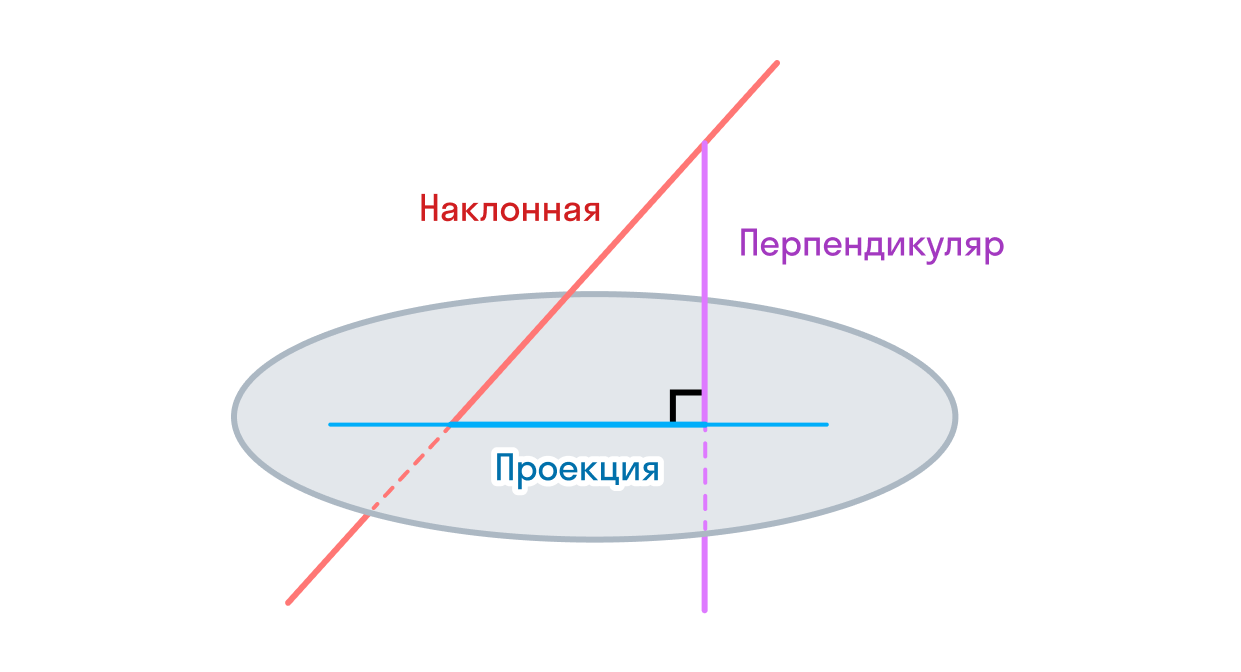
Пример 1: Рассмотрим плоскость ABCD и прямую М, которая пересекает эту плоскость. Угол между прямой М и плоскостью ABCD будет равен углу между прямой М и перпендикуляром, опущенным из любой точки этой прямой на плоскость ABCD. Для определения этого угла, можно воспользоваться формулой cos(α) = |(a1 * a2 + b1 * b2 + c1 * c2)| / (sqrt(a1^2 + b1^2 + c1^2) * sqrt(a2^2 + b2^2 + c2^2)), где а1, b1, c1 — координаты векторов, задающих прямую М, а а2, b2, c2 — координаты нормального вектора к плоскости ABCD.
-
Пример 2: Рассмотрим плоскость P и прямую l, которая находится внутри этой плоскости. Угол между прямой l и плоскостью P равен нулю, так как прямая лежит полностью внутри плоскости и не пересекает ее.
-
Пример 3: Рассмотрим плоскость Q и прямую m, которая параллельна ей. Угол между прямой m и плоскостью Q также будет равен нулю, так как прямая и плоскость не пересекаются и расположены параллельно друг другу.
Это лишь некоторые примеры, которые помогут понять определение угла между прямой и плоскостью.
Угол между наклонной прямой и горизонтальной плоскостью
Угол между наклонной прямой и горизонтальной плоскостью может быть измерен в градусах, радианах или любой другой удобной системе измерения углов. Этот угол может быть положительным или отрицательным, в зависимости от направления наклона прямой.
Примером угла между наклонной прямой и горизонтальной плоскостью может служить наклонная линия, проведенная на земле, например, наклонная стенка дома. Угол наклона этой стенки относительно горизонтальной плоскости будет являться углом между наклонной прямой и горизонтальной плоскостью.
Знание угла между наклонной прямой и горизонтальной плоскостью имеет большое практическое значение в различных областях, таких как строительство, геодезия, архитектура и другие.
Изучение угла между наклонной прямой и горизонтальной плоскостью позволяет определить, насколько отклонена прямая от горизонтального положения и какова ее ориентация относительно горизонта.
Важно отметить, что угол между наклонной прямой и горизонтальной плоскостью может быть как остроугольным, так и тупоугольным, в зависимости от угла наклона прямой.
Угол между вертикальной прямой и плоскостью
Угол между вертикальной прямой и плоскостью может быть измерен с помощью геометрических методов или с использованием специальных инструментов, таких как угломер или уровень. Значение угла будет зависеть от положения плоскости относительно прямой: если плоскость полностью параллельна вертикальной прямой, то угол будет равен 0 градусов; если плоскость перпендикулярна вертикальной прямой, то угол будет равен 90 градусов.
Примером ситуации, когда важно знать угол между вертикальной прямой и плоскостью, является строительство зданий. Архитекторы и инженеры используют этот угол для определения вертикальности стен и определения уровня, что является важным для обеспечения безопасности и качества строительных работ.
В геодезии и навигации также используется угол между вертикальной прямой и плоскостью для определения ориентации карт и планов относительно местности. Это помогает визуализировать и интерпретировать информацию, содержащуюся на картах, что является важным для навигации и планирования маршрутов.
Важно отметить, что для определения угла между вертикальной прямой и плоскостью необходимо иметь точную систему координат и точные измерения. Это позволяет получить точные значения угла и использовать его в различных областях, требующих знания ориентации плоскостей и прямых относительно друг друга.
Угол между прямой и наклонной плоскостью
Угол между прямой и наклонной плоскостью определяется как угол между прямой, лежащей в плоскости, перпендикулярной наклонной плоскости, и направляющим вектором этой прямой.
Для определения угла между прямой и наклонной плоскостью используется формула:
cos(α) = |n * a| / (|n| * |a|)
где α — угол между прямой и наклонной плоскостью, n — нормальный вектор плоскости, a — направляющий вектор прямой.
Зная значения векторов n и a, можно вычислить значение угла α.
Например, пусть у нас есть наклонная плоскость, заданная уравнением: 3x + 2y + z = 1, и прямая, заданная параметрическими уравнениями: x = 1 + t, y = 2 — t, z = 3 + 2t. Нормальный вектор плоскости будет равен n = (3, 2, 1), а направляющий вектор прямой будет равен a = (1, -1, 2).
Подставляя значения в формулу, получаем: cos(α) = |(3, 2, 1) * (1, -1, 2)| / (|(3, 2, 1)| * |(1, -1, 2)|) = 9 / √15 * √6 = 9 / √90 ≈ 0.9487.
Итак, угол α между прямой и наклонной плоскостью составляет примерно 0.9487 радиан или примерно 54.47°.
Зная значение угла α, можно решать различные задачи, связанные с взаимным расположением прямой и наклонной плоскости, например, определить, пересекаются ли они, параллельны ли или образуют ли прямую и плоскость зигзагообразную форму.
Практическое применение определения угла между прямой и плоскостью
Одним из примеров применения этого определения является аэронавигация. В аэронавигации угол между наклонной плоскостью крыла самолета и осью характеризует угол атаки. Этот угол влияет на подъемную силу, динамику полета и управляемость самолета. Измерение и коррекция угла атаки играют важную роль в обеспечении безопасности полетов и оптимизации аэродинамических характеристик самолетов.
В области компьютерного графического моделирования и визуализации также используется определение угла между прямой и плоскостью. Например, в трехмерной графике при построении трехмерных объектов и их текстур, угол между нормалью поверхности и лучом света определяет освещение объекта и создает эффекты тени и отражения. Точное определение угла между прямой и плоскостью позволяет создавать реалистичные визуальные эффекты и достичь высокой степени детализации в компьютерной графике.
Еще одним практическим применением определения угла между прямой и плоскостью является геодезия. В геодезии угол между наклонной плоскостью земной поверхности (наклон к вертикали) и направлением линии связи между двумя геодезическими пунктами измеряется с помощью теодолита. Такие измерения используются для определения высоты и геометрических характеристик местности, планирования строительных проектов и создания картографических материалов.
Таким образом, определение угла между прямой и плоскостью имеет широкое практическое применение в различных областях, где требуется анализ пространственных отношений и определение геометрических свойств объектов.
Вопрос-ответ:
Что такое угол между прямой и плоскостью?
Угол между прямой и плоскостью — это угол между прямой, проходящей через точку пересечения плоскости с нормалью плоскости, и самой плоскостью.
Как определить угол между прямой и плоскостью?
Угол между прямой и плоскостью можно определить с помощью формулы: угол равен арккосинусу абсолютной величины скалярного произведения вектора нормали плоскости на вектор направления прямой.
В чем особенности определения угла между прямой и плоскостью?
Особенностью определения угла между прямой и плоскостью является то, что этот угол может быть от 0 до 180 градусов. Также, если прямая перпендикулярна плоскости, угол между ними будет равен 90 градусам.
Как найти угол между прямой и плоскостью, заданными уравнениями?
Для нахождения угла между прямой и плоскостью, заданными уравнениями, нужно сначала определить вектор нормали плоскости и вектор направления прямой. Затем, используя формулу, вычислить угол.
Можете привести примеры угла между прямой и плоскостью?
Конечно! Например, если прямая задана уравнением x + y = 1, а плоскость уравнением x + y + z = 2, то угол между ними можно найти и он будет равен 43.59 градусам. Второй пример: прямая задана уравнением 2x — y = 0, плоскость — 2x + y + z = 1. Угол между ними будет равен 118.71 градусам.
Как определить угол между прямой и плоскостью?
Угол между прямой и плоскостью определяется как угол между прямой, лежащей в плоскости, и нормалью к этой плоскости. Для этого можно использовать формулу: угол = arccos(|n * d| / (|n| * |d|)), где n — вектор нормали к плоскости, d — вектор направления прямой.
В каких случаях угол между прямой и плоскостью будет прямым?
Угол между прямой и плоскостью будет прямым в случае, когда прямая перпендикулярна плоскости, то есть ее направляющий вектор параллелен вектору нормали плоскости. Также угол между прямой и плоскостью будет прямым, если вектор направления прямой параллелен плоскости.