Деление – одно из основных арифметических действий, которое позволяет разделить одно число на другое. Результатом деления является частное – число, которое получается при делении одного числа на другое.
Для обозначения деления используется знак «/», который читается как «разделить на». Например, 10/2 означает, что число 10 нужно разделить на число 2.
Чтобы понять, что называется результатом деления, необходимо знать некоторые особенности этой операции. Во-первых, делить можно только на ненулевое число. Результатом деления на ноль является неопределенность или бесконечность, что не имеет смысла в контексте обычной арифметики.
Раздел 1: Определение и основные понятия
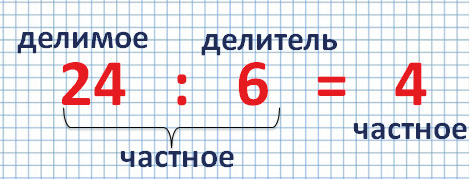
Результатом деления является число, называемое частным. Делитель — это число, на которое осуществляется деление, а делимое — число, которое делится на делитель.
Деление основано на двух важных понятиях: частное и остаток. Частное — это результат деления, а остаток — это число, оставшееся после вычитания кратной части от делимого.
Деление может быть описано с помощью таблицы деления. В таблице деления делитель записывается под делимым числом, а результат разделения и остаток записываются в столбце справа. При выполнении деления важно проверить полученное частное, умножив его на делитель и прибавив остаток. Это должно давать изначальное делимое.
| Делимое | Делитель | Частное | Остаток |
| 12 | 4 | 3 | 0 |
Подраздел 1.1: Результат деления и его смысл
В математике результат деления обозначается символом «/», который разделяет делимое и делитель. Например, деление числа 10 на число 2 обозначается как 10 / 2 и имеет результат равный 5.
Результат деления имеет свой смысл в различных областях применения математики и науки. Например, в финансовой аналитике результат деления может использоваться для расчета процентной ставки, прибыльности или других финансовых показателей.
В программировании и компьютерных науках результат деления может быть использован для решения задач, связанных с обработкой данных, алгоритмами и моделированием.
Результат деления также может быть представлен в виде десятичной или дробной десятичной формы, а в некоторых случаях может быть округлен до определенного числа знаков после запятой.
Важно помнить, что в некоторых случаях результат деления может быть округлен или приведен к целочисленному значению, в зависимости от контекста задачи и требований.
| Пример | Делимое | Делитель | Частное |
|---|---|---|---|
| Пример 1 | 10 | 2 | 5 |
| Пример 2 | 7 | 3 | 2.3333 |
| Пример 3 | 9 | 4 | 2.25 |
Подраздел 1.2: Делимое и делитель
Делимое — это число, которое мы делим на делитель. В математических операциях обозначается символом доллара ($a$).
Делитель — это число, на которое делим делимое. Он обозначается символом знака деления (:) или через дробь (a/b), где a — делимое, а b — делитель.
Деление является одной из основных арифметических операций и позволяет нам выполнять различные вычисления, такие как распределение и пропорции. Результат деления может быть как целым числом, так и десятичной дробью.
Важно помнить, что при делении на ноль (0) результатом будет бесконечность или неопределенность.
Раздел 2: Примеры результатов деления
В этом разделе приведены несколько примеров результатов деления.
- Пример 1: Результат деления числа 10 на 2 равен 5.
- Пример 2: Результат деления числа 15 на 3 равен 5.
- Пример 3: Результат деления числа 20 на 4 равен 5.
Как видно из этих примеров, результат деления состоит из делимого, делителя и частного.
Обозначается деление символом «/», например 10 / 2 = 5.
Важно помнить, что результатом деления всегда является число!
Подраздел 2.1: Целочисленное деление
Целочисленное деление обозначается символом «//», и применяется к двум операндам — делимому и делителю. Например, если мы разделим число 10 на 3 с помощью целочисленного деления, результат будет равен 3, так как 3 * 3 = 9, и остаток это 10 — 9 = 1, который игнорируется при целочисленном делении.
Важно понимать, что при целочисленном делении результат всегда округляется вниз. Это означает, что если есть дробная часть от деления, она будет отброшена, а результат будет ближайшим меньшим целым числом.
Например, если мы разделим число -10 на 3 с помощью целочисленного деления, результат будет равен -4, так как 3 * -4 = -12, и остаток это -10 — (-12) = 2, который игнорируется при целочисленном делении. Из-за округления вниз, результат -4 будет ближайшим меньшим целым числом.
Подраздел 2.2: Десятичная дробь и бесконечная десятичная дробь
Например, число 3,14 является десятичной дробью, где 3 — целая часть числа, а 14 — дробная часть числа.
Однако, не все десятичные дроби являются конечными. Некоторые десятичные дроби могут иметь бесконечное количество десятичных разрядов. Такие числа называются бесконечными десятичными дробями.
Бесконечные десятичные дроби обычно записываются в виде бесконечной последовательности цифр в скобках или с троеточием в конце, указывая, что дробная часть продолжается далее.
Например, число π (пи) представляется в виде бесконечной десятичной дроби: 3,1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679…
Деление может привести к получению бесконечной десятичной дроби, если дробь не имеет конечного представления в десятичной системе счисления.
Раздел 3: Возможные варианты и особенности результатов
Возможные варианты результатов деления:
| Делимое число | Делитель | Частное | Остаток |
| 12 | 3 | 4 | 0 |
| 10 | 4 | 2 | 2 |
| 15 | 5 | 3 | 0 |
В приведенных примерах видно, что в первом случае результатом деления числа 12 на 3 является частное 4 без остатка. Во втором случае деление числа 10 на 4 дает частное 2 с остатком 2. В третьем случае деление числа 15 на 5 также дает частное 3 без остатка.
Особенности результатов деления:
1. Если число делится нацело без остатка, то результатом деления будет целое число, часто именуемое частным.
2. Если число не делится нацело и имеется остаток, то результатом деления будет десятичная дробь, состоящая из целой части и десятичных знаков, часто называемая десятичным частным.
3. Если делитель равен нулю, то деление будет невозможно, так как деление на ноль не определено математически.
4. Если делимое число равно нулю, то результат деления всегда будет нулем.
Понимание возможных вариантов и особенностей результатов деления поможет легче интерпретировать и использовать полученные числовые значения в дальнейших математических операциях или в реальной жизни.
Подраздел 3.1: Неполное или остаточное деление
Остаток от деления обычно обозначается символом «%», который располагается между делимым и делителем. Например, если мы разделим число 7 на 2, то получим результат равный 3, с остатком 1. Таким образом, результатом деления 7 на 2 будет 3, а остаток будет равен 1.
Неполное деление является важным понятием в математике и арифметике. Оно позволяет решать различные задачи, связанные с распределением объектов или количества на группы или порции. Например, при делении пиццы на одинаковые кусочки, неполное деление позволяет определить количество полученных кусочков и остаток пиццы, который при этом остается.
Остатки от деления могут быть разными и иметь различные значения. Они также можно использовать в дальнейших вычислениях или анализе данных. Например, в программировании остатки от деления широко применяются для определения четности или нечетности числа, а также для обработки массивов данных или циклических операций.
Важно помнить, что неполное деление может быть не всегда представлено в виде десятичной дроби. Например, при делении 7 на 3, результатом будет 2 с остатком 1. Однако, результат деления можно представить и в виде обыкновенной дроби, что будет являться другим способом записи данного деления.
Подраздел 3.2: Деление на ноль и бесконечность
Деление на ноль является математической ошибкой и не имеет смысла в большинстве случаев. Например, если у нас есть 10 яблок и мы хотим разделить их на 0 корзин, это не имеет смысла, так как невозможно разделить яблоки на несуществующие корзины.
Деление на ноль также может привести к ошибкам в программировании. В большинстве языков программирования при попытке разделить число на ноль будет сгенерировано исключение или вызвана ошибка во время выполнения программы. Это помогает предотвратить некорректные вычисления и проблемы с памятью.
В некоторых случаях, деление на ноль может давать специальные результаты. Например, если число бесконечность делить на другое число, результатом будет ноль. Также, если отрицательное число делится на ноль, результатом будет отрицательная бесконечность.
Вопрос-ответ:
Что такое результат деления?
Результат деления — это число или значение, полученное в результате операции деления двух чисел.
Как называется число, которое получается в результате деления?
Это число называется частным. Частное — это результат деления одного числа на другое.
Что означает остаток от деления?
Остаток от деления — это число, которое остается, когда одно число делится на другое и результат не является целым числом. Остаток представляет собой «остаток» или «неполное» количество.
Что происходит, когда одно число делится на другое без остатка?
Если одно число делится на другое без остатка, то результат деления является целым числом, то есть не имеет дробной части.