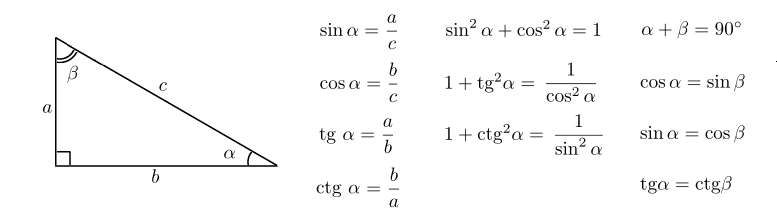
Тангенс — это одна из основных тригонометрических функций, которая позволяет определить соотношение между катетом прямоугольного треугольника и прилежащим к нему острым углом. Эта функция широко используется в различных сферах, включая физику, инженерию, геометрию и информатику.
Определение тангенса основывается на соотношении между длинами двух катетов прямоугольного треугольника и значением тангенса острого угла. Тангенс угла А в прямоугольном треугольнике определяется как отношение противолежащего катета к прилежащему катету. То есть, если А — острый угол, то тангенс А равен отношению длины противолежащего катета к длине прилежащего катета.
Тангенс часто обозначается как tg(A) или tan(A), где A — острый угол прямоугольного треугольника. Он может быть определен как вещественное число или как отношение двух длин. Значение тангенса изменяется от -∞ до +∞, и его точное значение зависит от величины угла А.
Тангенс и его определение
Тангенс угла A обозначается как tg(A) или tan(A).
Формула для определения тангенса в прямоугольном треугольнике:
- Выберите один из острых углов треугольника, например, угол A.
- Найдите длину противолежащего катета и длину прилежащего катета, относящиеся к углу A.
- Разделите длину противолежащего катета на длину прилежащего катета.
- Полученное значение является тангенсом угла A.
Тангенс имеет ряд важных свойств и связей с другими тригонометрическими функциями, что делает его полезным инструментом при решении геометрических и физических задач.
Зная значение тангенса, можно определить угол, используя обратную функцию тангенса — арктангенс (atan или tan-1).
Таким образом, знакомство с понятием тангенса и его определением позволяет более глубоко изучать геометрию и различные области науки, где требуется анализ треугольников и углов.
Что такое тангенс?
Формула для нахождения тангенса:
- Тангенс угла θ равен отношению длины противоположного катета (противолежащего углу) к длине прилежащего катета:
- тан(θ) = противоположный катет / прилежащий катет
- или
- тан(θ) = ½б (противоположный катет / прилежащий катет)
Знание тангенса угла позволяет нам определить длину одного из катетов прямоугольного треугольника, когда известны длины двух других сторон.
Тангенс является одной из основных тригонометрических функций и часто используется в физике, инженерии и других областях науки для решения проблем, связанных с треугольниками и углами.
Определение тангенса
Для определения тангенса угла в прямоугольном треугольнике необходимо знать длины противоположего и прилежащего катетов. Тангенс угла можно выразить с помощью формулы:
| Формула для определения тангенса |
|---|
| tan(α) = противоположный катет / прилежащий катет |
Тангенс является безразмерной величиной и может принимать положительные и отрицательные значения в зависимости от расположения угла относительно осей координат.
Определение тангенса в прямоугольном треугольнике позволяет вычислять значение этой функции и использовать ее в различных математических и инженерных задачах.
Математическое обозначение тангенса
Для прямоугольного треугольника со сторонами a, b и гипотенузой c, тангенс угла α будет равен tg(α) = a/b или tan(α) = a/b.
Тангенс помогает определить величину угла в треугольнике, когда известны длины двух его сторон. Эта функция широко применяется в различных областях науки и техники, включая физику, инженерию и дизайн.
Тангенс в прямоугольном треугольнике
Для нахождения тангенса в прямоугольном треугольнике необходимо возьмите противоположенный катет и разделить на прилежащий катет:
- Противоположенный катет — это сторона треугольника, расположенная напротив угла, для которого вы хотите найти тангенс.
- Прилежащий катет — это сторона треугольника, которая прилегает к углу, для которого вы хотите найти тангенс.
Формула для вычисления тангенса выглядит следующим образом:
Tan(угол) = Противоположенный катет / Прилежащий катет
Например, если у нас есть прямоугольный треугольник со сторонами 3 и 4, и мы хотим найти тангенс угла A, мы можем рассчитать:
Tan(A) = 3 / 4 = 0,75
Таким образом, тангенс угла A равен 0,75.
Тангенс и прямоугольный треугольник
Для нахождения значения тангенса нужно знать значения длин двух сторон треугольника — противолежащей и прилежащей сторон. Если противолежащая сторона обозначается как a, а прилежащая сторона — как b, то значение тангенса обозначается как tg и вычисляется по следующей формуле:
tg = a/b
Чтобы найти угол, значение тангенса которого известно, можно воспользоваться обратной функцией — арктангенсом. Арктангенс — это обратная функция тангенсу, которая позволяет найти угол, значение тангенса которого равно заданной величине.
Тангенс и арктангенс широко применяются не только в геометрии, но и в физике, инженерии, экономике и других областях науки и техники.
Прямоугольный треугольник и его стороны
Помимо гипотенузы, в прямоугольном треугольнике есть еще две стороны — катеты. Катеты прямоугольного треугольника примыкают к прямому углу и составляют с гипотенузой острые углы.
Обозначим катеты буквами a и b, а гипотенузу — буквой c.
Катеты прямоугольного треугольника связаны между собой и с гипотенузой с помощью тригонометрических функций — синуса, косинуса и тангенса. Определение тангенса заключается в отношении длины противолежащего катета к длине прилежащего катета:
tan(угол) = противолежащий катет / прилежащий катет
Таким образом, зная длины катетов, можно определить значение тангенса угла в прямоугольном треугольнике.
Определение тангенса в прямоугольном треугольнике
Для определения тангенса в прямоугольном треугольнике используется формула:
tg(α) = a / b
где α — угол между гипотенузой и прилежащим катетом, a — противоположенный катет, b — прилежащий катет.
Тангенс позволяет нам выразить отношение высоты радиана на горизонтальную ось прямоугольного треугольника. Значение тангенса может быть положительным, отрицательным или нулевым, в зависимости от угла α.
Используя тангенс, мы можем решать задачи на нахождение неизвестных сторон и углов прямоугольного треугольника, а также применять его в различных физических и геометрических задачах.
Вопрос-ответ:
Что такое тангенс?
Тангенс — это одна из тригонометрических функций, которая определяется как отношение длины противоположего катета к длине прилежащего катета в прямоугольном треугольнике. Тангенс применяется для вычисления углов и длин сторон треугольника.
Как определить тангенс в прямоугольном треугольнике?
Для определения тангенса в прямоугольном треугольнике необходимо взять длину противоположего катета и разделить ее на длину прилежащего катета. Полученное отношение будет являться значением тангенса для данного угла треугольника.
Как вычислить значение тангенса в треугольнике?
Для вычисления значения тангенса в треугольнике необходимо взять длину противоположего катета и разделить ее на длину прилежащего катета. Если у вас уже известны значения углов треугольника, то для каждого угла можно вычислить соответствующее значение тангенса.
Зачем нужен тангенс в прямоугольном треугольнике?
Тангенс в прямоугольном треугольнике используется для вычисления углов, длин сторон и построения прямоугольных треугольников. Эта тригонометрическая функция позволяет связать длины сторон треугольника с углами, что является основой для решения различных геометрических задач.