Параллельные прямые – это две прямые, которые не пересекаются ни в одной точке. Они всегда находятся на одном и том же расстоянии друг от друга и никогда не пересекаются. Такие прямые можно найти в различных геометрических фигурах, таких как прямоугольники, квадраты и параллелограммы.
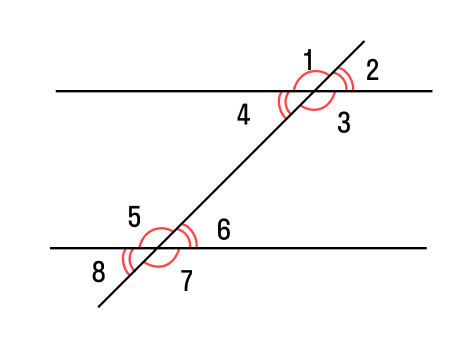
Определить, являются ли две прямые параллельными, можно по определенным критериям. Во-первых, для этого нужно проверить, что углы, образованные этими прямыми и пересекаемой ими прямой, сумма которых составляет 180 градусов, равны между собой. Если этот критерий выполняется, то прямые являются параллельными.
Во-вторых, можно провести перпендикулярную линию к одной из параллельных прямых. Если она пересекает другую прямую под прямым углом, то прямые являются параллельными.
Параллельные прямые обладают свойством, что все линии, проведенные между ними, вписываются в углы, равные между собой. Это свойство является основой для решения различных геометрических задач, таких как построение параллельных прямых, нахождение высоты или основания в треугольнике и т.д.
Понятие параллельных прямых
Параллельными прямыми называются прямые, которые не пересекаются и не имеют общих точек. В геометрии параллельные прямые можно определить несколькими способами.
Один из способов — использование определения параллельных прямых через углы. Две прямые являются параллельными, если и только если углы, образованные ими с любой третьей прямой, равны между собой. Например, если при пересечении двух прямых с третьей прямой образовались углы A и B, и эти два угла равны между собой, то прямые считаются параллельными.
Другой способ — использование определения параллельных прямых через расстояние. Две прямые являются параллельными, если и только если расстояние между ними постоянно и не меняется. Если существует точка на одной прямой и расстояние от этой точки до другой прямой остается постоянным, то прямые считаются параллельными.
Определение параллельных прямых может быть также связано с системой координат и угловым коэффициентом прямых. Если угловые коэффициенты двух прямых равны, то они являются параллельными.
| Способ определения | Термин |
|---|---|
| Через углы | Угловое определение |
| Через расстояние | Дистанционное определение |
| Через угловой коэффициент | Коэффициентное определение |
Что такое параллельные прямые
Для того чтобы определить, являются ли две прямые параллельными, необходимо выполнить следующее условие:
Если две прямые пересекаются в одной или нескольких точках, то они не являются параллельными.
Если две прямые лежат в одной плоскости и не пересекаются ни в одной точке, то они являются параллельными.
Два простых способа определения параллельности прямых:
- Сравнение углов. Если угол между прямыми равен 180 градусам (прямой угол), то они параллельны.
- Использование свойств параллельных прямых. Например, если прямые пересекают третью прямую так, что углы при пересечении с ней одинаковые (поперечные углы), то они параллельны.
Знание о параллельных прямых имеет большое значение в геометрии, инженерии и других областях, где требуется работа с прямыми и плоскостями. Параллельные прямые позволяют строить параллельные отрезки, определять углы и проводить различные исследования геометрических объектов.
Определение параллельных прямых
Параллельными прямыми называются две прямые, которые лежат в одной плоскости и не пересекаются ни в одной точке. Такие прямые имеют одинаковый угловой коэффициент, то есть их наклонные прямые имеют одинаковый угол наклона.
Для определения параллельных прямых можно использовать несколько методов. Один из них — это сравнение углов наклона. Если угловые коэффициенты двух прямых равны, то они являются параллельными.
Если известны координаты двух точек на каждой из прямых, можно воспользоваться формулой для определения углового коэффициента прямой:
k = (y2 — y1) / (x2 — x1)
где k — угловой коэффициент, а (x1, y1) и (x2, y2) — координаты точек на прямой.
Если угловые коэффициенты двух прямых равны, то эти прямые параллельны. Если же угловые коэффициенты различаются, то прямые пересекаются в одной точке.
Таким образом, определение параллельных прямых сводится к сравнению углов наклона или угловых коэффициентов этих прямых. Это позволяет нам легко определить, являются ли две прямые параллельными или нет.
Свойства параллельных прямых
1. Угол между параллельными прямыми равен нулю: Если две прямые параллельны, то угол между ними равен нулю. Это означает, что прямые не пересекаются и расположены строго параллельно друг другу.
2. Пропорциональность отрезков: Если на параллельных прямых провести перпендикуляры к третьей прямой, то отрезки, образованные этими перпендикулярами, будут пропорциональны.
3. Равенство внутренних углов: Две параллельные прямые накрест через пересекающую прямую создают равные внутренние углы. То есть, если две параллельные прямые пересекаются третьей прямой, то соответствующие внутренние углы равны.
4. Равенство внешних углов: Две параллельные прямые накрест через пересекающую прямую создают равные внешние углы. То есть, если две параллельные прямые пересекаются третьей прямой, то соответствующие внешние углы равны.
5. Равенство смежных углов: Две параллельные прямые, пересекаемые третьей прямой, создают равные смежные углы. То есть, смежные углы, образованные при пересечении параллельных прямых и третьей прямой, являются равными.
Как определить параллельные прямые
| Условие | Способ определения |
| 1. Прямые имеют одинаковый наклон | Проверьте, что у обеих прямых коэффициенты наклона равны. |
| 2. Прямые перпендикулярны одной и той же прямой | Убедитесь, что у обеих прямых произведения коэффициентов наклона равны -1. |
| 3. Прямые параллельны плоскости | Проверьте, что обе прямые лежат в одной плоскости и не пересекаются. |
Если все условия выполняются, то можно сказать, что прямые параллельны. Если прямые не отвечают ни одному из указанных условий, то они не являются параллельными.
Методы определения параллельных прямых
1. Метод с использованием углов. Для этого метода необходимо знание углов между прямыми. Если углы, образованные прямыми с третьей прямой (называемой трансверсальной), равны, то эти прямые параллельны.
2. Метод использования коэффициентов наклона. Коэффициент наклона прямой представляет собой отношение изменения y-координаты к изменению x-координаты. Если две прямые имеют одинаковый коэффициент наклона, то они параллельны.
3. Метод использования уравнений прямых. Если уравнения двух прямых имеют одинаковые коэффициенты, то прямые параллельны. Например, если уравнения прямых имеют вид y = mx + b, где m — коэффициент наклона, а b — свободный член, и коэффициенты m у этих уравнений равны, то прямые параллельны.
4. Метод использования точек пересечения. Если две прямые пересекаются с третьей прямой, то линии, проходящие через эти точки пересечения и параллельные данной третьей прямой, являются параллельными.
Выбор метода определения параллельных прямых зависит от доступных данных и условий задачи. Комбинирование разных методов может дать более точный результат.
Метод Соколя и Бозоты
Метод основан на том факте, что если две прямые параллельны, то углы, образованные этими прямыми и прямыми-пересекающими их, будут равными. Иными словами, две параллельные прямые имеют равные ориентированные углы с любой третьей прямой.
Для определения параллельности прямых с помощью метода Соколя и Бозоты необходимо провести проверку ориентированных углов.
- Выбираем точку M, лежащую на первой прямой.
- Проводим вторую прямую через точку M.
- Выбираем любую точку N, лежащую на второй прямой.
- Проводим третью прямую через точку N и первую выбранную точку M.
- Измеряем углы, образованные каждой из трех прямых.
Если углы, образованные первой и второй прямыми, и первой и третьей прямыми, равны между собой, то это означает, что первая и вторая прямые параллельны.
Метод Соколя и Бозоты является достаточно простым и надежным способом определения параллельности прямых. Он позволяет с высокой точностью установить, являются ли две прямые параллельными или нет.
Метод Углов
Для определения параллельности прямых с помощью метода Углов необходимо провести пересекающуюся с ними прямую и измерить углы, образованные этой прямой с обеими параллельными прямыми. Если эти углы оказываются равными, то это значит, что прямые параллельны.
Метод Углов является достаточно простым и удобным способом определения параллельности прямых. Он может быть использован, например, для проверки прямых линий на карте или на плоских поверхностях.
Важно отметить, что метод Углов не является абсолютно точным и может давать неточные результаты в случае несовершенных измерений или влияния других факторов. Поэтому при определении параллельности прямых с помощью метода Углов следует быть внимательным и учитывать возможные погрешности.
Вопрос-ответ:
Что такое параллельные прямые?
Параллельные прямые — это две прямые, которые никогда не пересекаются, независимо от их продолжения в бесконечность.
Как определить, что две прямые параллельны?
Для определения параллельности двух прямых можно использовать несколько методов. Один из них — проверка коэффициентов наклона прямых. Если коэффициенты наклона равны, то прямые параллельны. Еще один метод — использование свойства параллельных прямых: если две прямые пересекают третью прямую под одинаковым углом, то они параллельны. Также можно использовать геометрическую конструкцию с помощью углов и параллельных линий.
Можно ли параллельные прямые быть наклонными?
Да, параллельные прямые могут быть наклонными. Параллельность прямых определяется не только по их наклону, но и по их направлению. Даже если две прямые имеют разный наклон, они все равно могут быть параллельны, если они идут в одном направлении и никогда не пересекаются.
Как построить параллельную прямую к заданной прямой?
Для построения параллельной прямой к заданной прямой необходимо использовать геометрические конструкции. Один из способов — построение на основе параллельных перенесенных отрезков. Другой способ — построение параллельной прямой с использованием углов. Можно также использовать специальные инструменты, такие как параллельный циркуль или параллельные линейки, для точного построения параллельной прямой.
Как проверить, что две прямые параллельны на координатной плоскости?
Для проверки параллельности двух прямых на координатной плоскости необходимо проверить равенство их коэффициентов наклона. Если коэффициенты наклона равны, то прямые параллельны. Для этого можно воспользоваться формулой нахождения коэффициента наклона прямой: k = (y2 — y1) / (x2 — x1), где (x1, y1) и (x2, y2) — любые точки на прямой. Если значения коэффициентов наклона совпадают, то прямые параллельны.
Как определить параллельные прямые?
Параллельные прямые — это прямые, которые никогда не пересекаются. Определить, являются ли две прямые параллельными, можно с помощью аналитической геометрии. Если уравнения этих прямых имеют одинаковые коэффициенты при x и y, то они параллельны.
Что значит, если две прямые параллельны?
Если две прямые параллельны, это значит, что они никогда не пересекаются. Такие прямые идут вдоль друг друга, но никогда не сближаются. Геометрически, это выглядит так, что параллельные прямые расположены на одной плоскости и имеют одинаковое направление.