
Деление — это математическая операция, в ходе которой одно число, называемое делимым, делится на другое число, называемое делителем. Частное — результат деления, а остаток — число, оставшееся после вычета одного числа из другого. В процессе деления возникают разные числа и термины, которые описание каждого нам поможет лучше понять эту операцию.
Делимое — это число, которое делится на другое число. Оно аналогично делимому в делении. Делимое можно обозначать как х или а, в зависимости от контекста. Например, если мы делим число 12 на 3, то делимое — 12. Также делимое может быть представлено как разность двух чисел, например, в выражении 20-8=12, делимое равно 12.
Делитель — это число, на которое делится делимое. Он аналогичен делителю в делении. Делитель также может быть обозначен как у или b, в зависимости от контекста. Например, в делении 12 на 3, делитель — 3. Также делитель может быть представлен как отношение чисел в виде a:b или a/b.
Частное — это результат деления делимого на делитель. Оно обозначается q или r в зависимости от контекста. Например, в делении числа 12 на 3, частное равно 4. Частное может быть целым числом или десятичной дробью, и в зависимости от этого можно использовать разные обозначения для него.
Что такое числа в делении?
Когда два числа делятся друг на друга и остаток равен нулю, говорят, что они являются числами в делении. Например, если число 10 делится на число 2, результатом будет число 5, и мы можем сказать, что 10 и 2 – числа в делении.
Делимое
Делимое – это число, которое делится на другое число. Это число находится перед знаком деления и является результатом деления. В примере выше, где число 10 делится на число 2, делимым будет число 10.
Делитель
Делитель – это число, на которое делится делимое. Это число находится после знака деления. В примере выше, где число 10 делится на число 2, делителем будет число 2.
Числа в делении являются важными элементами математики и широко используются в различных областях, таких как финансы, наука и технологии. Понимание и правильная работа с числами в делении позволяют производить точные вычисления и анализировать данные.
Какие бывают числа в делении?
При делении чисел существует несколько видов чисел, которые могут быть получены в результате операции деления. Рассмотрим каждый из них:
| Вид числа | Описание |
|---|---|
| Целое число | Целое число получается, когда результат деления двух чисел без остатка. Например, 12 делить на 3 равно 4, что является целым числом. |
| Десятичная дробь | Десятичная дробь — это результат деления чисел с остатком, который не является нулевым. Например, 7 делить на 2 равно 3.5, где 3 — целая часть, а 0.5 — десятичная дробь. |
| Бесконечная десятичная дробь | Если результат деления чисел не имеет ограниченного числа десятичных знаков и не повторяется, то это бесконечная десятичная дробь. Например, 1 делить на 3 равно 0.33333…, где цифра 3 повторяется бесконечно. |
| Натуральная дробь | Натуральная дробь получается при делении нецелого числа на натуральное число. Например, 1.5 делить на 2 равно 0.75, где 0.75 — натуральная дробь. |
Все эти виды чисел имеют свои особенности и используются в различных математических и практических задачах.
Целая часть
Целая часть имеет большое значение при работе с длинными числами или в задачах, где нужно определить количество целых единиц, полученных в результате деления. Она может быть полезна при округлении числа в меньшую сторону и при использовании дробей в математических операциях.
Дробная часть
Дробная часть числа в делении представляет собой часть числа после запятой или десятичного разделителя. Она состоит из чисел, расположенных справа от запятой и указывает на доли целого числа.
Дробная часть числа может быть конечной или бесконечной, и она может быть представлена как периодическая десятичная дробь, так и непериодическая десятичная дробь.
Периодическая десятичная дробь имеет повторяющуюся последовательность цифр после запятой, например, 0,3333…, где тройка повторяется бесконечно. Непериодическая десятичная дробь не имеет повторяющейся последовательности цифр, например, 0,123456789.
Пример использования
Рассмотрим пример деления числа 7 на число 3. Результатом деления будет 2,3333…
| Число | Целая часть | Дробная часть |
|---|---|---|
| 7 | 2 | 0,3333… |
В данном примере, целая часть числа равна 2, а дробная часть представлена периодической десятичной дробью 0,3333…
Что означает неполное деление?
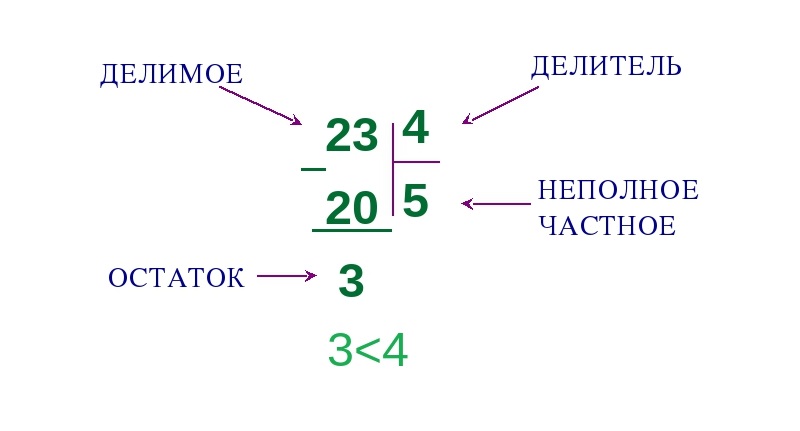
Когда выполняется неполное деление, делимое обозначается числом исходного значения и записывается над чертой, а делитель — числом, на которое делимое делится, и записывается под чертой. Затем производится действие деления, которое может быть выполнено вручную или с помощью калькулятора.
Результатом неполного деления является десятичная дробь, которая может быть представлена в виде конечной или бесконечной десятичной дроби, и, возможно, с остатком. Если десятичная дробь имеет ограниченное количество знаков после запятой, она называется конечной. Если десятичная дробь повторяется бесконечно или имеет бесконечное количество знаков после запятой, она называется бесконечной.
Неполное деление широко используется в различных областях, таких как финансы, наука, технологии и строительство. Например, в финансах неполное деление может использоваться для рассчета процентных ставок и долей. В науке неполное деление может использоваться для решения задач, связанных с величинами, измеряемыми в десятичных дробях. В технологиях неполное деление может использоваться для рассчета размеров компонентов и значений параметров. В строительстве неполное деление может использоваться для рассчета длин и площадей.
Что такое остаток от деления?
Основная формула для нахождения остатка от деления выглядит так: остаток = делимое — делитель * целая часть от деления.
Остаток от деления широко используется в математике, программировании и других областях. Он позволяет определить, есть ли остаток или нет, и может использоваться для различных целей.
Примеры остатка от деления:
- При делении числа 10 на число 3 остаток равен 1. То есть, 10 = 3 * 3 + 1.
- При делении числа 15 на число 5 остаток равен 0. То есть, 15 = 5 * 3 + 0.
- При делении числа -7 на число 2 остаток равен -1. То есть, -7 = 2 * -4 + -1.
Свойства остатка от деления:

Остаток от деления обладает следующими свойствами:
- Остаток всегда неотрицательный, то есть он может быть равен нулю или больше нуля.
- Остаток всегда меньше делителя.
- Остаток от деления двух положительных чисел всегда положителен.
- Остаток от деления положительного числа на отрицательное число всегда отрицателен.
- Остаток от деления отрицательного числа на положительное число всегда положителен.
- Остаток от деления отрицательного числа на отрицательное число может быть как положительным, так и отрицательным, в зависимости от чисел.
Знание остатка от деления позволяет решать задачи, которые связаны с распределением элементов, вычислением времени и другими математическими операциями. Оно также может быть полезным при настройке некоторых алгоритмов и программ.
Что такое частное от деления?
Чтобы получить частное, необходимо поделить делимое на делитель. Например, если у нас есть число 12 и мы хотим разделить его на число 3, то частное будет равно 4. В этом примере число 12 является делимым, число 3 — делителем, а число 4 — частным.
Частное от деления может быть как целым числом, так и десятичной дробью. Если результат деления является целым числом, то говорят, что деление было без остатка. Если же результат деления является десятичной дробью, то говорят, что деление было с остатком.
Когда мы вычисляем частное от деления, иногда интересным является не только сам результат, но и остаток от деления. Остаток от деления обозначает то число, которое остается после извлечения частного.
Частное от деления играет важную роль в различных областях математики, а также в повседневной жизни. Например, он используется для расчетов при проектировании и строительстве, для решения задач на доли и проценты, для получения среднего значения и многих других задач.
Как называются числа, на которые выполняется деление?
Целочисленное деление
Целочисленное деление выполняется между двумя целыми числами. Результатом целочисленного деления является целое число, не содержащее дробной части. Например, при делении числа 10 на 3, результатом будет число 3.
Вещественное деление
Вещественное деление выполняется между двумя вещественными числами. Результатом вещественного деления является число с десятичной дробью, которое может быть точным или округленным до определенного количества знаков после запятой. Например, при делении числа 10.5 на 3, результатом будет число 3.5.
Также можно рассматривать деление в других системах счисления, например, двоичной или шестнадцатеричной. В этом случае, аналогично, первое число будет делимым, второе — делителем, и результатом будет число в соответствующей системе счисления.
Деление является одной из основных арифметических операций и широко применяется в различных областях, например, в математике, физике, экономике и программировании.
| Математический символ | Обозначение операции деления |
|---|---|
| / | Деление числа на число |
| % | Деление с получением остатка |
| // | Целочисленное деление |
| : | Деление с записью дробной части |
Делимое
Делимое является одним из трех основных элементов деления. Остальные два элемента — это делитель и частное. Делитель — это число, на которое делится делимое. Частное — результат деления, то есть число, которое получается при выполнении операции деления.
Например, в выражении «12 ÷ 3 = 4» число 12 является делимым, так как оно делится на число 3 без остатка.
Делимое может быть положительным или отрицательным числом, а также может быть целым или десятичным числом. Например, числа 24, -36, 3.5 и -8.75 все являются делимыми.
Примеры
Вот несколько примеров использования термина «делимое»:
| Делимое | Делитель | Частное |
| 12 | 3 | 4 |
| -36 | 6 | -6 |
| 8.25 | 2.5 | 3.3 |
В этих примерах число 12, -36 и 8.25 являются делимыми, так как они делятся на свои делители без остатка.
Делитель
Все числа делятся на 1 и на само себя. Это значит, что 1 и само число являются делителями для любого числа. Кроме того, нуль не является делителем, потому что на ноль делить нельзя.
Делители положительных чисел могут быть только положительными числами, а делители отрицательных чисел могут быть как положительными, так и отрицательными.
Множество делителей числа называется делительным множеством. Число делителей можно выразить формулой: если число n разложить на простые множители в виде \(p_1^{\alpha_1} \cdot p_2^{\alpha_2} \cdot \ldots \cdot p_k^{\alpha_k}\), где \(p_1, p_2, \ldots, p_k\) – простые числа, а \(\alpha_1, \alpha_2, \ldots, \alpha_k\) – их степени, то количество делителей числа n будет равно \((\alpha_1+1)(\alpha_2+1)\ldots(\alpha_k+1)\).
Например, у числа 12 есть делители: 1, 2, 3, 4, 6, 12. Оно разлагается на простые множители в виде \(2^2 \cdot 3^1\), а количество делителей равно \((2+1)(1+1) = 6\).
Делители играют важную роль в различных областях математики, таких как теория чисел, алгебра и геометрия. Они используются для нахождения кратных чисел, нахождения наибольшего общего делителя и других математических операций.
Вопрос-ответ:
Что такое делимое?
Делимое — это число, которое делится на другое число без остатка.
Что такое делитель?
Делитель — это число, на которое делится другое число без остатка.
Что такое частное?
Частное — это результат деления одного числа на другое число, полученное без остатка.
Что такое остаток?
Остаток — это число, которое остается после деления одного числа на другое числом нацело. То есть, если при делении 12 на 5 мы получаем частное 2 и остаток 2, то число 2 и будет остатком.