Геометрия – это один из разделов математики, который изучает различные фигуры, их свойства и взаимное размещение. Одним из основных понятий в геометрии является угол. Угол – это область плоскости, ограниченная двумя лучами, которые имеют общее начало и называются сторонами угла. В зависимости от взаимного положения сторон угла, они могут иметь разные названия.
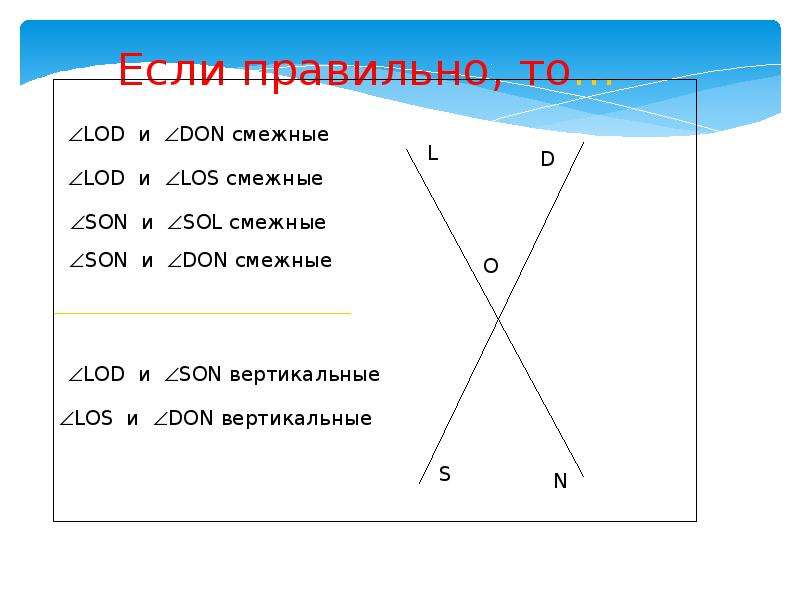
Один из типов углов, названный в программе геометрии 7 класса, – это смежные углы. Смежные углы – это два угла, которые имеют общую сторону и общую вершину, но не пересекаются. Другими словами, смежные углы находятся на одной стороне от общей стороны и образуют линию.
Особенностью смежных углов является то, что их сумма равна 180 градусов. Доказательство этого факта состоит в том, что линия, на которой находятся смежные углы, является прямой линией, которая сама по себе образует угол в 180 градусов. Поэтому, если мы разделим этот угол на два смежных угла, их сумма также будет равна 180 градусам. Это является основным свойством смежных углов и используется при решении различных задач в геометрии.
Геометрия 7 класс: основные понятия и определения
В 7 классе основные понятия и определения в геометрии включают в себя:
1. Углы
Угол — это геометрическая фигура, образованная двумя лучами (сторонами угла), которые имеют общее начало (вершину угла). Углы могут быть различными по величине и положению. В геометрии выделяют несколько видов углов, включая:
| Название угла | Описание |
|---|---|
| Прямой угол | Угол, равный 90 градусам. Прямой угол обозначается символом ∠. |
| Тупой угол | Угол, больший 90 градусов и меньше 180 градусов. Тупой угол обозначается символом ∠. |
| Острый угол | Угол, меньший 90 градусов. Острый угол обозначается символом ∠. |
Смежные углы — это два угла, имеющих общую вершину и общую сторону, но не перекрывающиеся. Они расположены рядом друг с другом и образуют пару углов.
2. Фигуры и их свойства
Геометрия 7 класс также включает в себя изучение различных геометрических фигур и их свойств. Важные определения в этой области включают:
- Треугольник — фигура, состоящая из трех сторон и трех углов.
- Четырехугольник — фигура, состоящая из четырех сторон и четырех углов.
- Правильный многоугольник — многоугольник, у которого все стороны и все углы равны между собой.
Кроме того, в геометрии изучаются свойства различных фигур, таких как равенство сторон и углов, параллельность сторон и перпендикулярность.
Понятие угла в геометрии
Виды углов
- Острый угол — угол, меньший прямого угла (меньше 90 градусов).
- Прямой угол — угол, равный 90 градусам.
- Тупой угол — угол, больший прямого угла (больше 90 градусов).
- Равный угол — два угла, которые имеют одинаковую величину.
- Смежные углы — углы, имеющие общую сторону и общую вершину, но не перекрывающиеся.
- Вертикальные углы — два угла, образованные пересечением двух прямых линий. Вертикальные углы равны друг другу.
Понимание и умение работать с углами важно при решении различных задач геометрии и при изучении различных свойств геометрических фигур.
Смежные углы: что это такое и как определить
Смежными углами называются два угла, которые имеют общую вершину, общую сторону и не пересекаются.
Чтобы определить, являются ли два угла смежными, необходимо проверить, имеют ли они общую вершину и общую сторону, а также не пересекаются ли они другими углами.
Для наглядного представления смежных углов и их свойств можно использовать таблицу.
| Смежные углы | Свойства |
|---|---|
| Угол ABC и угол CBD | Общая вершина: B Общая сторона: BC |
| Угол ABD и угол DBE | Общая вершина: B Общая сторона: BD |
| Угол CBE и угол EBD | Общая вершина: B Общая сторона: BE |
Зная определение и свойства смежных углов, можно решать задачи по геометрии, например, найти значение неизвестного угла в треугольнике или многоугольнике.
Таким образом, понимание смежных углов и умение определять их помогут в изучении геометрии и решении соответствующих задач.
Какие углы называются смежными
Смежные углы могут быть как двухугольными, так и многоугольными. Они могут быть как остроугольными, так и тупоугольными.
Смежные углы дополняют друг друга до 180 градусов. Если сумма двух смежных углов равна 180 градусов, то они называются дополнительными (дополняющими) углами. В этом случае, каждый из смежных углов является дополнительным углом для другого.
Примеры смежных углов:
- Угол ABD и угол CBD являются смежными углами, так как они имеют общую сторону AB и общую вершину B.
- Угол XYP и угол PYZ являются смежными углами, так как они имеют общую сторону YZ и общую вершину Y.
Свойства смежных углов:
- Смежные углы имеют общую сторону и общую вершину.
- Сумма смежных углов равна 180 градусов.
- Если угол А и угол В смежные, и угол В и угол С смежные, то угол А и угол С также смежные.
Смежные углы являются важным понятием в геометрии и используются для решения различных задач, таких как расчеты в треугольниках, прямоугольниках и других фигурах.
Свойства смежных углов в геометрии
Одно из основных свойств смежных углов — их сумма всегда равна 180 градусам. Это свойство называется линейной парой углов. Если два угла являются смежными и их сумма равна 180 градусам, то они называются линейными углами.
Также, если смежные углы являются вертикальными, то они равны между собой. Вертикальные углы образуются пересечением двух прямых линий и имеют одинаковую меру. Другими словами, если два смежных угла являются вертикальными углами, то их меры равны.
Свойства смежных углов в геометрии помогают упростить задачи и делают геометрические построения более точными. Понимание этих свойств позволяет решать задачи по вычислению меры углов и строить различные фигуры.
Примеры задач по определению и свойствам смежных углов
Пример 1:
На рисунке представлены две пары смежных углов. Найдите значение каждого угла.
- Угол AOB = 60°
- Угол BOC = 120°
- Угол COD = 40°
- Угол DOA = ?
Решение: Угол DOA можно найти, вычитая из 360° сумму других углов, смежных с DOA.
Угол DOA = 360° — (Угол AOB + Угол BOC + Угол COD) = 360° — (60° + 120° + 40°) = 360° — 220° = 140°
Пример 2:

На рисунке представлен отрезок AB и точки C и D такие, что AD является продолжением отрезка AB. Найдите значение угла ADC.
- Угол ADE = 80°
- Угол BDC = 60°
- Угол CDA = ?
Решение: Угол CDA можно найти, используя свойство смежных углов. Угол BDC и угол ADC являются смежными углами и имеют общую сторону CD.
Угол CDA = Угол BDC = 60°
Приведенные выше примеры демонстрируют применение определения и свойств смежных углов для решения различных задач по геометрии. Зная эти свойства, можно более точно определить значения углов и строить правильные геометрические конструкции.
Как использовать знание смежных углов в решении задач
Для использования этого знания в задачах, необходимо понимать некоторые основные свойства смежных углов:
| Свойство | Описание |
|---|---|
| Сумма смежных углов | Сумма двух смежных углов всегда равна 180 градусам. Другими словами, если имеется пара смежных углов, то их сумма всегда будет равна 180 градусам. |
| Внешний угол | Внешний угол, образованный продолжением одной из сторон смежного угла и другой стороной, равен сумме двух смежных углов. |
| Углы при параллельных прямых | Если две прямые параллельны, то соответственные углы и смежные углы равны. |
Используя эти свойства, можно решать различные задачи, например:
1. Найти неизвестный угол, используя сумму смежных углов.
2. Найти неизвестный угол, используя внешний угол и известные смежные углы.
3. Доказать, что прямые параллельны, используя равные смежные углы.
Знание о смежных углах может быть полезным не только при решении геометрических задач, но и при построении и анализе геометрических фигур. Правильное использование этого знания поможет более точно и эффективно решать задачи и получать правильные результаты.
Вопрос-ответ:
Какие углы называются смежными?
Смежными называются углы, у которых общая сторона и вершина.
Какие свойства имеют смежные углы?
Смежные углы равны между собой и дополняют друг друга до 180 градусов.
Можно ли у смежных углов одинаковое измерение?
Да, смежные углы могут быть равными, если они имеют одинаковую меру.
Какие углы не являются смежными?
Углы, у которых нет общей стороны или вершины, не являются смежными.
Что произойдет, если сложить два смежных угла?
Если сложить два смежных угла, получится угол, равный их сумме.
Какие углы называются смежными?
Смежными называются два угла, имеющие общую сторону и общую вершину.
Как определить, что углы смежные?
Чтобы определить, что углы смежные, нужно проверить, есть ли у них общая сторона и общая вершина.