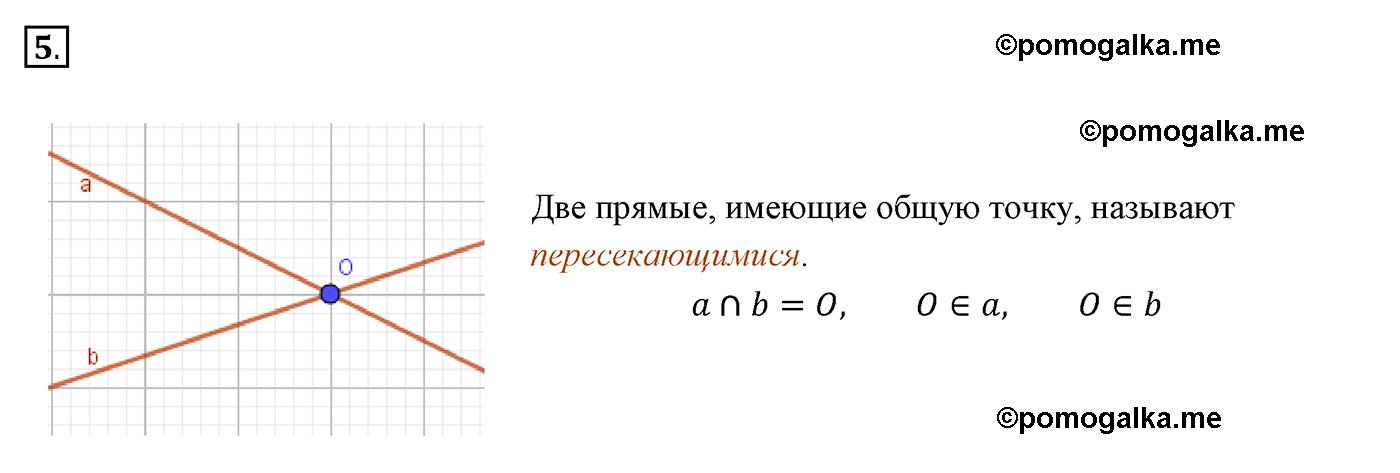
Один из основных понятий геометрии — пересечение двух прямых. Но что имеется в виду, когда говорят, что две прямые пересекаются? Две прямые считаются пересекающимися, если они имеют одну и только одну общую точку. Именно на этом принципе строится множество задач и теорем, связанных с пересечением прямых.
Пересечение двух прямых — это ключевое понятие в аналитической геометрии. Однако, оно также широко используется и во многих других областях. Например, пересечение линий на дороге — это один из основных моментов, при котором водитель принимает решение о дальнейшем движении. Грамотное владение знанием о пересечении прямых помогает не только в понимании окружающего мира, но и в решении повседневных задач.
Если две прямые пересекаются, то в точке их пересечения образуется угол. Точку пересечения принято обозначать буквой А, угол — буквой В. Это необходимо для дальнейшего рассмотрения свойств и закономерностей, которые возникают при пересечении прямых. Знание этих особенностей позволяет находить решения задач, связанных с пересечением прямых, а также проводить анализ и построение графиков.
Что такое пересекающиеся прямые
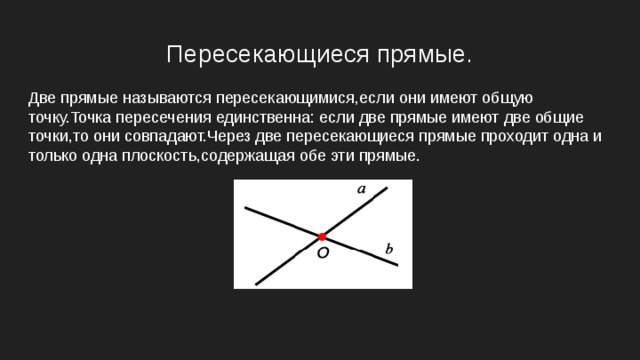
Когда две прямые пересекаются, они образуют углы. Эти углы могут быть разной величины и могут быть использованы для определения относительного положения прямых друг относительно друга.
Кроме того, пересечение двух прямых является основой для решения задач о нахождении координат точки пересечения, нахождения углов между прямыми и много других геометрических задач.
Пересекающиеся прямые — это одно из основных понятий геометрии, которое находит применение во многих областях науки и техники.
Способы задания прямых:
Прямые в геометрии могут быть заданы различными способами. Некоторые из наиболее распространенных способов задания прямых включают:
- Задание прямой через две точки.
- Задание прямой через точку и направляющий вектор.
- Задание прямой через уравнение, их формулу или параметрическое уравнение.
Задание прямой через две точки является наиболее простым способом. Для этого необходимо указать координаты двух различных точек, через которые проходит прямая. Прямая определена единственным образом, если указаны две разные точки.
Задание прямой через точку и направляющий вектор также является распространенным способом. Для этого необходимо указать координаты одной точки, через которую проходит прямая, а также координаты вектора, указывающего направление прямой.
Задание прямой через уравнение, их формулу или параметрическое уравнение предусматривает использование математических уравнений или формул для определения прямой. Примеры таких уравнений включают уравнение вида y = mx + c, где m — это наклон (угловой коэффициент) прямой, а c — это свободный член, а также параметрическое уравнение вида x = at + b, y = ct + d, где a, b, c, d — это параметры прямой.
Системы прямых
Системы прямых представляют собой группу прямых, которые имеют общую точку пересечения. Эта точка называется точкой пересечения системы прямых.
Системы прямых могут иметь различные конфигурации в пространстве:
| 1. Параллельные прямые | Прямые, которые никогда не пересекаются и лежат в плоскостях, которые никогда не пересекаются друг с другом. |
| 2. Пересекающиеся прямые | Прямые, которые пересекаются в одной точке. |
| 3. Совпадающие прямые | Прямые, которые совмещаются и имеют бесконечное количество общих точек. |
| 4. Разнонаправленные прямые | Прямые, которые имеют противоположные направления и не имеют общих точек. |
Системы прямых играют важную роль в геометрии, физике, инженерии и других науках. Изучение и анализ систем прямых позволяет решать различные задачи, такие как построение геометрических фигур, определение расстояний, нахождение пересечений и т.д.
Количественные характеристики пересекающихся прямых
При пересечении двух прямых возникают некоторые количественные характеристики, которые могут быть полезны при решении геометрических задач и анализе графиков.
Угол пересечения: Если две прямые пересекаются, то они образуют угол пересечения, который измеряется в градусах. Этот угол может быть острый, прямой или тупой в зависимости от направления прямых и их взаимного положения.
Точка пересечения: При пересечении прямых они имеют общую точку, которая называется точкой пересечения. Координаты этой точки могут быть вычислены с использованием метода решения системы уравнений, задающих прямые.
Расстояние между прямыми: Расстояние между двумя пересекающимися прямыми может быть вычислено как расстояние от одной из прямых до точки пересечения. Это расстояние может быть положительным или отрицательным, в зависимости от того, с какой стороны от точки пересечения находится данная прямая.
Угол наклона прямой: Угол наклона прямой определяет ее наклон или уклон. Он измеряется отношением вертикального смещения (разницы между y-координатами двух точек на прямой) к горизонтальному смещению (разнице между x-координатами этих точек). Угол наклона может быть вычислен по следующей формуле: угол наклона = arctg(вертикальное смещение / горизонтальное смещение).
Свойства пересекающихся прямых
Основное свойство
Если две прямые пересекаются, то они не совпадают и не параллельны. То есть, они имеют общую точку, но не совпадают полностью.
Следствия
Из основного свойства пересекающихся прямых следуют несколько важных утверждений:
- Угол между двумя пересекающимися прямыми — это острый угол, прямой угол или тупой угол.
- Если две прямые пересекаются, то каждая из них делит другую на две части.
- Если две прямые пересекаются, то сумма всех углов, образованных ими на одной стороне пересечения, равна 180 градусов (это следует из свойства, что угол на прямой равен 180 градусов).
Знание свойств пересекающихся прямых позволяет решать различные задачи по геометрии, а также представляет основу для изучения других геометрических фигур и связанных с ними понятий.
Уравнение пересекающихся прямых
Уравнение прямой в общем виде имеет вид:
y = kx + b, где:
- y – значение y-координаты прямой
- k – угловой коэффициент прямой
- x – значение x-координаты прямой
- b – свободный член (смещение прямой по оси y)
При пересечении двух прямых, уравнения которых известны, необходимо найти их точку пересечения, то есть значения x и y для этой точки.
Решение системы уравнений прямых – это нахождение значений x и y, при которых оба уравнения выполняются одновременно. Это достигается путем решения уравнений относительно x и y и подстановки их значений в оба уравнения.
Таким образом, уравнение пересекающихся прямых можно получить путем решения системы уравнений прямых.
Пример:
Даны две прямые:
- Прямая 1: y = 2x + 1
- Прямая 2: y = -3x + 4
Для нахождения их пересечения, решим систему уравнений:
2x + 1 = -3x + 4
Перенесем все переменные в одну часть уравнения:
2x + 3x = 4 — 1
5x = 3
Выразим x:
x = 3/5
Теперь подставим найденное значение x в одно из уравнений:
y = -3(3/5) + 4 = -9/5 + 20/5 = 11/5
Итак, точка пересечения данных прямых имеет координаты (3/5, 11/5).
Формула вычисления точки пересечения
В геометрии, для нахождения точки пересечения двух прямых необходимо решить систему уравнений, описывающую данные прямые. Для этого можно воспользоваться методом подстановки или методом исключения.
Метод подстановки
Пусть уравнения прямых заданы в общем виде:
Прямая 1: Ax + By + C1 = 0
Прямая 2: Dx + Ey + C2 = 0
Для нахождения точки пересечения необходимо подставить одно уравнение в другое и решить полученное уравнение относительно одной переменной.
Если полученное уравнение имеет единственное решение, то найденные значения подставляем в исходные уравнения для определения координат точки пересечения.
Метод исключения
Пусть уравнения прямых заданы в общем виде:
Прямая 1: Ax + By + C1 = 0
Прямая 2: Dx + Ey + C2 = 0
Для нахождения точки пересечения необходимо умножить одно уравнение на коэффициент, так чтобы коэффициенты перед одной из переменных в двух уравнениях были равными с учетом знака.
После этого полученные уравнения суммируются или вычитаются друг из друга, чтобы исключить одну из переменных.
Подставляем найденное значение одной переменной в любое из исходных уравнений, чтобы определить координату другой переменной точки пересечения.
Решение задач с пересекающимися прямыми
Способы решения задач с пересекающимися прямыми:
1. Графический метод. Для решения задачи по графическому методу, необходимо построить графики данных прямых на координатной плоскости. Пересечение прямых на графике позволяет определить точку пересечения.
2. Аналитический метод. Для решения задачи по аналитическому методу, необходимо записать уравнения данных прямых и найти координаты точки пересечения, решив систему уравнений. Для этого можно использовать метод подстановки, метод сложения и вычитания или метод Крамера.
3. Использование связей между углами. В некоторых задачах можно использовать связи между углами, образованными пересекающимися прямыми. Например, если задача связана с нахождением значений углов, можно использовать свойства соответственных углов, вертикальных углов, углов секущей и хорды и т.д.
Решение задач с пересекающимися прямыми требует логического мышления, аккуратности и точности в работе. Важно понимать свойства и особенности пересечения прямых, а также уметь применять различные методы для решения задач.
Пример:
Даны две прямые y = 2x + 3 и y = -3x + 5. Найдите точку их пересечения.
Решение:
Для нахождения точки пересечения прямых, запишем систему уравнений:
2x + 3 = -3x + 5
5x = 2
x = 2/5
Подставим значение x в любое уравнение прямых:
y = 2(2/5) + 3 = 4/5 + 15/5 = 19/5
Точка пересечения прямых имеет координаты (2/5, 19/5).
Практическое применение
Знание того, что две прямые называют пересекающимися, имеет большое практическое применение в различных областях. Вот некоторые из них:
Геометрия
Понимание понятия пересекающихся прямых является основой геометрии. Оно позволяет анализировать и решать задачи, связанные с пересечением линий, отрезков и углов.
Архитектура и инженерия
Пересекающиеся прямые часто встречаются в архитектурных и инженерных проектах. Они используются для разметки зданий, конструкций и инфраструктуры, а также для определения точек пересечения и углов.
Важно помнить, что пересекающиеся прямые могут иметь различные свойства и характеристики, которые могут быть использованы в разных практических ситуациях. Поэтому знание о пересекающихся прямых может быть полезным как для профессионалов в области математики и физики, так и для широкой публики.
Примеры использования пересекающихся прямых в геометрии
1. Определение точки пересечения прямых.
Пересекающиеся прямые могут использоваться для определения точки, в которой они пересекаются. Для этого можно воспользоваться методом решения системы уравнений, представляющих уравнения данных прямых. Решив систему, можно найти координаты точки пересечения.
2. Решение геометрических задач.
Пересекающиеся прямые активно используются для решения различных геометрических задач. Например, задача о построении биссектрисы угла может быть решена с помощью пересекающихся прямых. Или задача о нахождении высоты треугольника может быть решена построением перпендикуляра, который пересекает сторону треугольника.
3. Построение пересекающихся прямых.
Построение пересекающихся прямых является одной из базовых задач геометрии. Этот прием позволяет решать множество задач, в которых необходимо определить взаимное расположение прямых и их точки пересечения. Пересекающиеся прямые можно построить с помощью циркуля и линейки или с использованием компьютерных программ.
4. Геометрическое моделирование.
Пересекающиеся прямые часто используются для моделирования различных объектов в геометрии. Например, в трехмерной геометрии пересекающиеся прямые могут быть использованы для создания трехмерных моделей и определения их формы и взаимного расположения.
Одной из ключевых концепций в геометрии является пересечение прямых. Они широко используются для решения задач, а также для создания моделей и определения формы объектов. Пересекающиеся прямые помогают нам лучше понять пространственные отношения и свойства геометрических фигур.
Вопрос-ответ:
Почему две прямые называют пересекающимися?
Две прямые называют пересекающимися, если они имеют общую точку пересечения. То есть, в точке, где они пересекаются, они имеют одни и те же координаты по осям x и y.
Как определить, пересекаются ли две прямые?
Для определения, пересекаются ли две прямые, необходимо уравнения этих прямых приравнять друг к другу и решить получившуюся систему уравнений. Если система имеет решение, то прямые пересекаются, если нет – значит, они не пересекаются.
Чем отличаются пересекающиеся прямые от параллельных?
Пересекающиеся прямые имеют общую точку пересечения и образуют угол, в то время как параллельные прямые не имеют общей точки пересечения и не образуют угла. Также уравнения пересекающихся прямых отличны друг от друга, в то время как уравнения параллельных прямых одинаковы.
Как найти координаты точки пересечения двух прямых?
Чтобы найти координаты точки пересечения двух прямых, необходимо решить систему уравнений, состоящую из уравнений этих прямых. Решив систему, получим значения x и y, которые будут являться координатами искомой точки пересечения.
Что такое пересекающиеся прямые?
Пересекающиеся прямые — это две прямые, которые имеют общую точку пересечения.