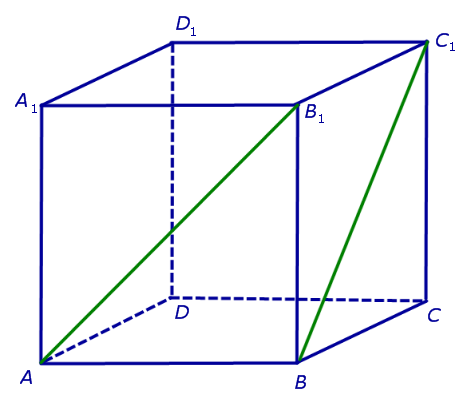
Две прямые называются скрещивающимися, когда они пересекаются друг с другом, образуя угол. Если две прямые пересекаются в одной точке, которая одновременно является началом и концом каждой из них, то они называются скрещивающимися прямыми.
Скрещивающиеся прямые могут обладать разными свойствами и использоваться в различных областях математики и естественных наук. Они могут строиться графически для визуализации геометрических конструкций, а также использоваться для задач моделирования и решения сложных проблем в различных научных дисциплинах.
Понимание скрещивающихся прямых и углов, которые они образуют, является важным основанием для изучения геометрии и алгебры. Изучение этих концепций помогает понять связь между различными фигурами и формами, а также развивает навыки решения проблем, аналитического мышления и логики.
Геометрическое представление скрещивающихся прямых
Две прямые называются скрещивающимися, если они пересекаются и не лежат в одной плоскости. Геометрическое представление скрещивающихся прямых может быть представлено следующим образом:
1. Пересечение точкой
Если две прямые пересекаются в одной точке, то они скрещиваются. При этом, координаты пересечения можно найти с помощью системы уравнений прямых.
2. Нет пересечения
Если две прямые не пересекаются, то они не скрещиваются. При этом, прямые могут быть параллельными или сонаправленными.
Параллельные прямые лежат в одной плоскости, но никогда не пересекаются. Они имеют одинаковый наклон и расстояние между ними постоянно.
Сонаправленные прямые также не пересекаются и лежат в одной плоскости. Они имеют одинаковый наклон, но необходимо проверить расстояние между ними для полного определения сонаправленности.
Как определить, являются ли две прямые скрещивающимися?
Шаг 1: Найдите точку пересечения
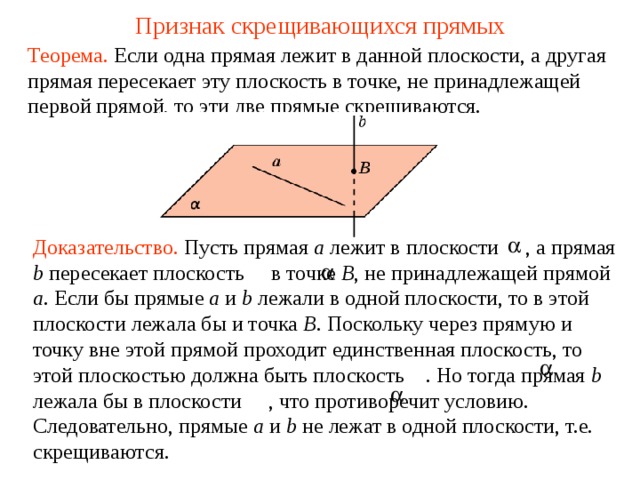
Для начала, определите координаты точек на обеих прямых. Далее, используйте формулы для нахождения координат точки пересечения двух прямых. Если полученные координаты одинаковы, значит, прямые пересекаются в одной точке.
Шаг 2: Проверьте лежащие стороны
Чтобы убедиться, что обе стороны угла, образуемого этими прямыми, лежат на одной плоскости, рассмотрим точку пересечения и другие точки на каждой прямой. Если все эти точки лежат на одной плоскости, то прямые скрещиваются.
| Прямая 1 | Прямая 2 |
|---|---|
| (x1, y1) | (x3, y3) |
| (x2, y2) | (x4, y4) |
Например, если на прямой 1 есть точки (x1, y1) и (x2, y2), и на прямой 2 есть точки (x3, y3) и (x4, y4), то точка пересечения будет иметь координаты (x5, y5). Проверьте, что все точки на прямой 1 и прямой 2, а также точка пересечения лежат на одной плоскости.
Если оба условия выполняются, прямые можно считать скрещивающимися. В противном случае, они не скрещиваются.
Особенности углов, образующихся между скрещивающимися прямыми
1. Смежные углы
Смежные углы — это пары углов, которые имеют общую вершину и общую сторону. В случае скрещивающихся прямых, углы, образованные между переменными прямыми, являются смежными. Это означает, что углы расположены рядом друг с другом и дополняют друг друга до 180 градусов. Например, если один угол составляет 40 градусов, то другой угол будет равен 140 градусам.
2. Сумма углов
Когда прямые линии скрещиваются, они образуют четыре угла в точке пересечения. Все эти углы в сумме дают 360 градусов. То есть, сумма всех углов, образованных между скрещивающимися прямыми, равна 360 градусам. Это свойство называется свойством суммы углов в точке пересечения.
Когда вы сталкиваетесь с проблемой нахождения неизвестного угла в системе скрещивающихся прямых, вы можете использовать эти свойства, чтобы легче решить задачу. Например, если известно значение одного угла, вы можете узнать значение другого, используя свойство суммы углов.
Признаки скрещивающихся прямых на координатной плоскости
Две прямые на координатной плоскости называются скрещивающимися, если они пересекаются в одной точке. Скрещивающиеся прямые имеют следующие признаки:
| Признак | Описание |
|---|---|
| Расположение коэффициентов | У скрещивающихся прямых коэффициенты перед переменными имеют разные знаки. |
| Пересечение с осями координат | Скрещивающиеся прямые пересекают ось абсцисс и ось ординат в разных точках. |
| Угловой коэффициент | Угловой коэффициент одной прямой положительный, а у другой прямой отрицательный. |
Если прямые имеют эти признаки, то они точно скрещиваются на координатной плоскости. Чтобы определить точку пересечения, можно решить систему уравнений, составленных по уравнениям прямых. Также можно построить график прямых и найти их пересечение графически.
Примеры задач, решаемых с использованием скрещивающихся прямых
1. Построение перпендикуляров
Используя скрещивающиеся прямые, можно легко построить перпендикуляр к данной прямой. Для этого необходимо провести скрещивающуюся прямую, а затем провести перпендикуляр к ней, проходящий через исходную прямую.
2. Нахождение точки пересечения
Два скрещивающихся прямых образуют точку пересечения. Эта точка может быть использована для решения множества задач, включая нахождение координаты этой точки или определение геометрического места точек, равноудаленных от данных прямых.
Примечание: Внимательно следите за тем, чтобы прямые действительно скрещивались, а не были параллельными или совпадающими. В противном случае, решение задачи может быть некорректным.
Практическое применение концепции скрещивающихся прямых
Концепция скрещивающихся прямых используется в различных областях науки и техники. Её практическое применение обнаружено в геометрии, физике, инженерии, компьютерной графике и других дисциплинах.
Геометрия
В геометрии концепция скрещивающихся прямых играет важную роль при решении задач на нахождение точек пересечения. Важно понимать, что скрещивающиеся прямые пересекаются в одной точке, не являются параллельными и не совпадают друг с другом. Это свойство позволяет использовать концепцию скрещивающихся прямых для нахождения неизвестных координат и углов.
Физика
В физике концепция скрещивающихся прямых помогает в определении траекторий движения объектов. Например, при анализе движения тел в пространстве можно применить данную концепцию для определения места столкновения двух тел, летящих по разным траекториям.
| Область | Пример практического применения |
|---|---|
| Инженерия | Определение точки пересечения двух дорог на проектировании перекрестков |
| Компьютерная графика | Отображение трехмерных объектов на двумерном экране с использованием пересечений линий |
В целом, концепция скрещивающихся прямых является важным инструментом в решении задач, связанных с нахождением точек пересечения и определением траекторий объектов.
Вопрос-ответ:
Что значит «скрещивающиеся строки»?
Скрещивающиеся строки — это две строки, которые пересекаются в определенной точке.
Какое условие должны удовлетворять прямые, чтобы можно было сказать, что они скрещиваются?
Для того чтобы две прямые можно было назвать скрещивающимися, они должны лежать в одной плоскости и пересекаться в одной точке.
Какие свойства имеют скрещивающиеся прямые?
Скрещивающиеся прямые являются несовпадающими и не параллельными. Они имеют общую точку пересечения и лежат в одной плоскости.
Что произойдет, если две прямые лежат в разных плоскостях?
Если две прямые лежат в разных плоскостях, то они не смогут пересечься и, следовательно, не будут скрещивающимися.