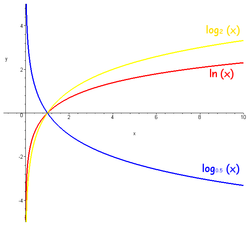
Логарифмической функцией называется функция, обратная к экспоненциальной функции. Она играет важную роль в математическом анализе и науках, связанных с измерениями. График логарифмической функции имеет свои особенности, которые интересны для изучения и понимания.
Ось абсцисс на графике логарифмической функции соответствует значениям аргумента функции, а ось ординат – значениям самой функции. Логарифмическая функция растет медленно вначале, но затем начинает возрастать более быстро. Это связано с ее свойством сжатия экспоненты – она сглаживает большие значения и усиливает малые.
На графике логарифмической функции можно выделить несколько особых точек. Например, точка (1, 0) обозначает, что логарифм от 1 равен 0. Это свойство является фундаментальным для всех логарифмических функций. Второй особой точкой является точка (0, -∞), которая показывает, что натуральный логарифм от 0 неопределен.
Логарифмы и логарифмические функции

Основные свойства логарифмов
- Логарифм числа a по основанию b обозначается как logba и определяется как показатель степени, в которую нужно возвести основание b, чтобы получить число a.
- Основание логарифма может быть любым положительным числом, кроме 1.
- Логарифм числа 1 по любому основанию равен 0, так как любое число возведенное в степень 0 равно 1.
- Логарифм от отрицательного числа или нуля не определен.
- Логарифмическая функция обладает свойством перестановки основания и аргумента: logba = logca / logcb.
Примеры логарифмических функций
- Общая форма логарифмической функции выглядит следующим образом: y = logbx, где y — значение функции, x — аргумент функции, b — основание логарифма.
- Наиболее распространенными основаниями логарифма являются 10 (десятичный логарифм), e (натуральный логарифм) и 2 (двоичный логарифм).
- Логарифмическая функция с основанием 10 получила название десятичного логарифма и обозначается как log(x).
- Натуральный логарифм, обозначаемый как ln(x), является частным случаем логарифмической функции с основанием e, где e — базовое математическое константа.
Логарифмические функции широко применяются для решения уравнений, моделирования роста и распада, описания исследовательских данных, а также в финансовых расчетах. Они играют важную роль в различных областях науки и практических приложений.
Определение логарифма
Если \(a^x = b\), то по определению логарифма выполняется равенство: \(x = \log_a{b}\), где \(a\) – основание логарифма.
То есть логарифм числа \(b\) по основанию \(a\) равен показателю степени \(x\), при котором \(a\) возводится в степень, равную числу \(b\).
Логарифмы широко применяются в различных областях науки и техники, таких как математика, физика, экономика, статистика и другие. Они являются важным инструментом для работы с числами, особенно с очень большими или очень малыми значениями, а также для решения экспоненциальных уравнений и построения логарифмических графиков.
Примеры логарифмических функций
1. Натуральный логарифм
Одной из наиболее известных логарифмических функций является натуральный логарифм, обозначаемый как ln(x). Он является обратной функцией экспоненциальной функции и показывает значение степени, в которую нужно возвести число e (приближенно равное 2,71828) для получения значения x.
Например, ln(2) равен около 0,693, так как 2 возводится в степень около 0,693, чтобы получить значение 2.
2. Общий логарифм
Также существует общий логарифм, обозначаемый как log(x). Он использует основание 10 и показывает значение степени, в которую нужно возвести 10, чтобы получить значение x.
Например, log(100) равен 2, так как 10 возводится в степень 2 для получения значения 100.
Кроме натурального и общего логарифма, существует множество других логарифмических функций, таких как двоичный логарифм, десятичный логарифм и другие, которые находят свое применение в различных областях науки и техники.
Особенности графиков логарифмических функций
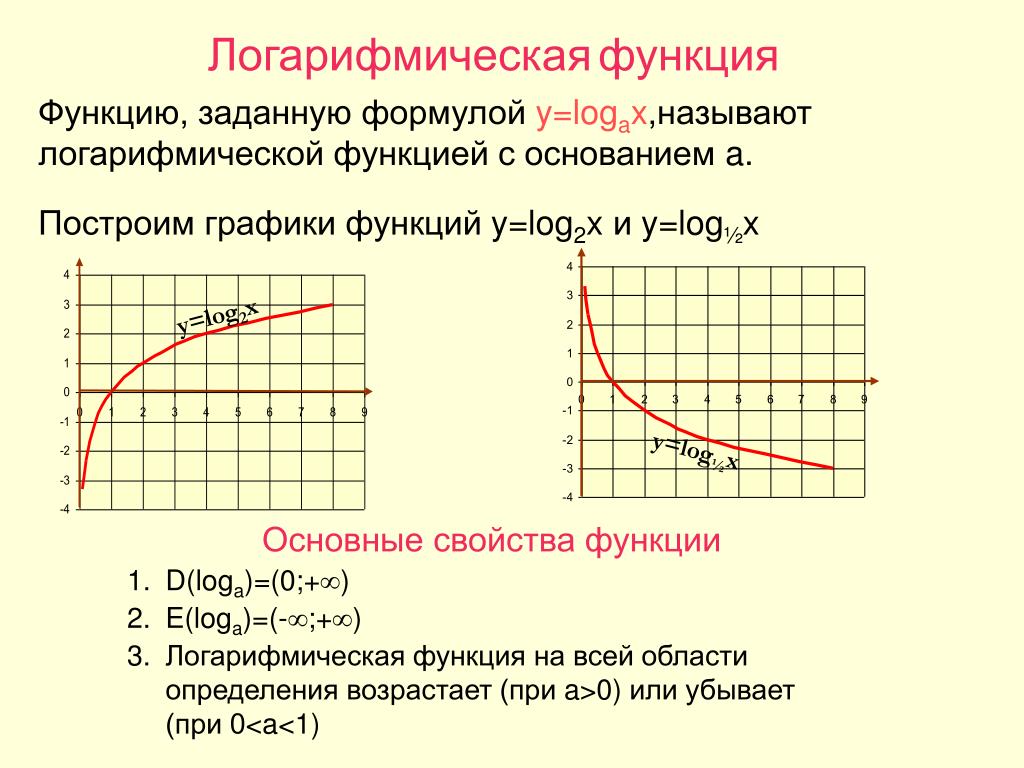
1. Прохождение через точку (1, 0)
Логарифмическая функция f(x) = logb(x) проходит через точку (1, 0) для любого основания b. Это связано с основным свойством логарифма: logb(b) = 1. Таким образом, значение функции равно 0 при аргументе 1.
2. Ограниченность графика
Логарифмическая функция не имеет определенного предела при аргументе, стремящемся к бесконечности. Однако график функции ограничен сверху горизонтальной прямой y = k, где k — любое положительное число.
| Основание b | Пример графика |
|---|---|
| b > 1 |  |
| 0 < b < 1 |  |
Таким образом, график логарифмической функции всегда лежит выше оси x и ограничен сверху горизонтальной прямой.
Знание особенностей графиков логарифмических функций позволяет анализировать и решать различные математические задачи, в которых участвуют логарифмические выражения и функции.
Чем отличается логарифмическая функция от обычной функции?
Основные отличия:
- Зависимость аргумента и значения: В отличие от обычной функции, значение логарифмической функции не зависит от значения самого аргумента, а определяется лишь его степенью в соответствии с выбранным основанием. Это означает, что одному и тому же значению аргумента могут соответствовать различные значения логарифмической функции в зависимости от выбранного основания.
- Ограничения: Обычная функция может принимать любые значения из определенного диапазона в зависимости от её определения. Логарифмическая функция же имеет определенные ограничения в значениях: она может быть определена только для положительных аргументов и выбранного основания. Для отрицательных аргументов и основания, логарифмическая функция не имеет определения.
Помимо этих двух основных отличий, логарифмическая функция имеет ряд дополнительных свойств и особенностей, которые делают её полезной в различных областях науки и инженерии.
| Тип функции | Зависимость аргумента и значения | Ограничения |
|---|---|---|
| Обычная функция | Значение зависит от аргумента | Может быть определена для любых значений |
| Логарифмическая функция | Значение зависит от степени аргумента | Может быть определена только для положительных аргументов и выбранного основания |
Свойства графиков логарифмических функций
1. Асимптоты
Логарифмические функции имеют вертикальные асимптоты, которые соответствуют вертикальным прямым линиям. Асимптота проходит через точку (0, 0) и имеет уравнение x = a, где a — это основание логарифма. Это означает, что график логарифмической функции стремится к этой вертикальной линии при приближении x к плюс или минус бесконечности.
2. Пересечения с осями координат
График логарифмической функции всегда пересекает ось OX в точке (1, 0) и ось OY в точке (0, b), где b — это значение, равное логарифму от основания логарифма. Другими словами, значение логарифма от базы является значением y-координаты точки пересечения графика с осью OY.
Эти особенности графиков логарифмических функций позволяют нам анализировать их свойства и использовать их в различных областях, таких как математика, физика, экономика и др.
Построение графиков логарифмических функций
Построение графиков логарифмических функций может быть полезно при решении различных математических и инженерных задач. Для построения графиков необходимо сначала определить область определения функции и изучить основные свойства логарифмической функции.
Одним из основных свойств логарифмической функции является то, что она проходит через точку (1, 0). Также важными особенностями графиков логарифмических функций являются симметрия графика относительно оси y = x и асимптоты.
Для построения графика логарифмической функции удобно использовать таблицу значений, где значения аргумента x выбираются в соответствии с областью определения функции.
Зная значения функции в таблице, можно построить график, отмечая на координатной плоскости полученные точки и соединяя их линией.
График логарифмической функции может иметь различные свойства в зависимости от основания логарифма и других параметров функции. Например, при основании логарифма b > 1, график функции будет возрастающей кривой, а при 0 < b < 1 - убывающей кривой.
Также важно отметить, что график логарифмической функции может пересекать оси координат и иметь точки перегиба.
Использование графиков логарифмических функций является мощным инструментом в различных областях, включая математику, физику, экономику и другие науки. Построение и анализ графиков логарифмических функций помогает в решении задач и изучении свойств различных математических моделей.
Практическое применение логарифмических функций
Одно из практических применений логарифмических функций состоит в решении задач, связанных с экспоненциальным ростом и убыванием. Например, логарифмические функции широко используются в финансовой математике для расчета сложных процентов и анализа инвестиционных проектов. Они позволяют оценивать доли изменений величин, а также управлять ставками процента и финансовыми инструментами.
Логарифмические функции также применяются в физике для моделирования различных процессов. Например, они помогают в описании распределения энергии в спектрах, характеристиках затухания сигналов, процессов диффузии и теплообмена. Они также используются в медицине для математического моделирования химических реакций и фармакокинетических процессов.
Логарифмические функции находят применение в геологии и геофизике для изучения различных явлений, таких как землетрясения, извержения вулканов и движение плит земной коры. Они позволяют строить модели и предсказывать различные геологические процессы.
В области информационных технологий логарифмические функции используются для решения задач о сложности алгоритмов, оптимизации работы программ и анализа сложных систем. Они также находят применение в статистике, эконометрике и машинном обучении для обработки больших объемов данных и построения предсказательных моделей.
Кроме того, логарифмические функции используются в различных естественных науках, включая биологию, химию, астрономию и экологию. Они помогают в анализе данных, построении графиков, моделировании различных процессов и решении сложных задач.
Таким образом, практическое применение логарифмических функций охватывает широкий спектр областей и помогает в решении различных задач. Понимание принципов работы и возможностей логарифмических функций является важным инструментом для специалистов во многих областях знаний.
Вопрос-ответ:
Что такое логарифмическая функция?
Логарифмическая функция — это функция, обратная к экспоненциальной функции. Она задается уравнением y = loga(x), где a — основание логарифма.
Чем отличается график логарифмической функции от графика других функций?
График логарифмической функции имеет особенности, которые делают его отличным от графиков других функций. Например, график логарифмической функции может иметь асимптоты, вертикальные асимптоты и точки перегиба.
Какие свойства имеет график логарифмической функции?
График логарифмической функции имеет следующие свойства: он всегда лежит выше оси абсцисс, асимптоты графика являются наклонными прямыми, а его симметричность относительно оси ординат зависит от основания логарифма.
Какие примеры логарифмических функций вы знаете?
Примеры логарифмических функций включают натуральный логарифм, двоичный логарифм, десятичный логарифм и логарифм по любому другому базису.
Можете дать пример графика логарифмической функции?
Конечно! Например, график функции y = log2(x) — это кривая, которая начинается из точки (1, 0), проходит через точку (2, 1), (4, 2) и так далее. Он имеет вертикальную асимптоту в x = 0 и убывает при стремлении x к бесконечности.
Что такое логарифмическая функция?
Логарифмическая функция — это функция, обратная к экспоненциальной функции. Она описывает зависимость между аргументом (обычно положительными числами) и значением функции.
Каким образом строится график логаримической функции?
График логарифмической функции строится с использованием набора точек, полученных путем подстановки различных значений аргумента. Затем эти точки соединяются ломаной линией, которая и представляет собой график функции.