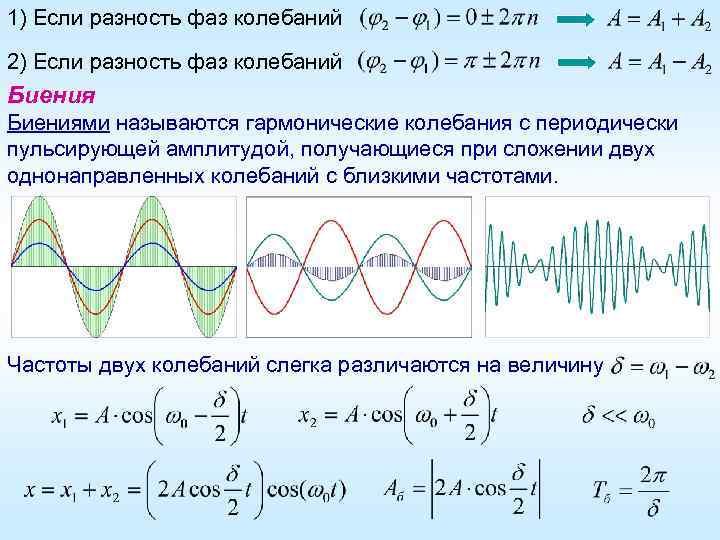
Механическими колебаниями называют процесс периодического повторения движения вокруг равновесного положения. Они являются одной из основных форм движения в физике и широко применяются в различных областях науки и техники. Механические колебания можно наблюдать в жизни каждый день — от маятников часов до колебания струн музыкальных инструментов.
Одним из ключевых понятий в изучении механических колебаний является равновесие. Равновесие достигается при отсутствии внешних сил, которые бы влияли на систему, и когда система находится в стабильном состоянии. Если из системы уводят и возвратно-поступательно, то действующая на нее сила восстанавливает исходное положение, что и приводит к колебаниям.
Важную роль в механических колебаниях играют параметры системы, такие как амплитуда — максимальное смещение системы от положения равновесия, период — время, за которое система совершает одно полное колебание, и частота — обратная величина периода. Эти параметры описывают процесс колебаний и позволяют изучать их свойства и законы.
Определение и примеры
Механическими колебаниями называют периодические изменения положения или состояния физической системы вокруг равновесного состояния. Данный процесс характеризуется периодичностью и повторяемостью.
Примеры механических колебаний:
- Маятник — это классический пример механических колебаний. Маятник представляет собой тяжелое тело, подвешенное на нити или стержне, которое может свободно колебаться в горизонтальной или вертикальной плоскости. Маятник обладает периодическими движениями, которые можно наблюдать, например, в часах.
- Колебания волны — это еще один пример механических колебаний. Волны могут быть продольными, когда частицы среды движутся вдоль направления распространения волны, или поперечными, когда частицы среды движутся перпендикулярно направлению распространения волны. Волны могут распространяться в различных средах, таких как вода, воздух или твердые тела.
- Колебания пружины — растяжение или сжатие пружины вызывает ее колебания. Пружины используются во многих механизмах и устройствах, например в амортизаторах автомобилей или в игрушках, чтобы создать эффект упругого движения.
- Затухающие колебания — это механические колебания, которые со временем затухают и останавливаются. Например, когда вы стреляете из ружья, пуля начинает затухающие колебания по горизонтальной оси и, в конечном итоге, полностью останавливается.
Механические колебания широко встречаются в физических системах и имеют множество практических применений, что делает их важной темой в области физики и инженерии.
Типы механических колебаний
Механические колебания в физике подразделяются на несколько основных типов, в зависимости от характера движения и системы:
Свободные колебания
Свободные колебания отличаются отсутствием внешнего воздействия на систему. Это колебания, возникающие только в результате начальных условий и передвигающиеся без внешней силы.
Вынужденные колебания
Вынужденные колебания возникают под действием внешней силы, которая регулярно изменяет характер движения системы. Эта сила может быть периодической или апериодической.
В зависимости от конкретной системы и условий, свободные и вынужденные колебания могут проявляться в различных формах и иметь различные свойства. Например, они могут быть гармоническими или нелинейными, амплитуда и период колебаний могут меняться во времени, и т.д.
Изучение различных типов механических колебаний позволяет понять и описать много различных физических систем и явлений, будь то колебания пружин или электрических цепей, маятников или атомов.
Уравнение гармонического колебания
Механическими колебаниями называют периодические движения, в которых тело осуществляет повторяющиеся изменения положения относительно равновесного положения.
Одним из наиболее изучаемых типов механических колебаний является гармоническое колебание. Оно описывается уравнением, называемым уравнением гармонического колебания.
Уравнение гармонического колебания:
м d²x/dt² +
где м — масса колеблющегося тела, x — его координата относительно положения равновесия, t — время, а к0 — коэффициент жесткости среды, в которой происходят колебания. Уравнение гармонического колебания является дифференциальным уравнением второго порядка.
Решение этого уравнения позволяет определить зависимость координаты x тела от времени t и точно предсказать характеристики колебаний, такие, как амплитуда, частота и фаза колебаний.
Амплитуда и период колебаний
Амплитуда
Амплитуда колебаний (обозначается буквой A) – это максимальное отклонение объекта от его равновесного положения. Она характеризует «силу» или «интенсивность» колебаний, то есть насколько сильно объект движется относительно своего положения равновесия.
Амплитуда может быть измерена в различных физических величинах, в зависимости от типа колебаний. Например, для гармонических колебаний (когда объект движется вдоль прямой линии с постоянной частотой и амплитудой) амплитуда измеряется в метрах (м) или других единицах длины. Для крутильных колебаний (когда объект вращается вокруг оси) амплитуда измеряется в радианах (рад) или градусах (°).
Период
Период колебаний (обозначается буквой T) – это время, за которое объект выполняет одно полное колебание. Он определяется как обратное значение частоты (f) колебаний. То есть, период можно выразить формулой:
T = 1/f
Период измеряется в секундах (с) или других единицах времени. Он также может быть записан в виде количества колебаний в единицу времени, например, в герцах (Гц). Герц – это единица измерения частоты, равная одному колебанию в секунду.
Период и частота колебаний связаны обратной пропорциональностью. Чем меньше период, тем выше частота, и наоборот.
| Тип колебаний | Единица измерения амплитуды | Единица измерения периода |
|---|---|---|
| Гармонические колебания | метры (м) или другие единицы длины | секунды (с) |
| Крутильные колебания | радианы (рад) или градусы (°) | секунды (с) |
Фазовая плоскость и фазовая траектория
Фазовая траектория представляет собой кривую на фазовой плоскости, описывающую изменение состояния системы во времени. Каждая точка на фазовой траектории соответствует определенному состоянию системы в конкретный момент времени. Фазовая траектория может быть замкнутой, когда система периодически повторяет свое состояние, или не замкнутой, когда система не имеет периодических колебаний.
Фазовая плоскость и фазовая траектория являются важными инструментами для анализа и понимания динамики механических систем. Они позволяют визуализировать и предсказывать поведение системы и определять её устойчивость. Изучение фазовой плоскости и фазовых траекторий позволяет улучшить понимание колебательных процессов и применять полученные знания в различных областях науки и техники.
Декремент затухания и резонанс
Механическими колебаниями называют периодически повторяющееся движение тела вокруг положения равновесия. В процессе колебаний возникают явления, такие как декремент затухания и резонанс.
Декремент затухания — это уменьшение амплитуды колебаний со временем. Оно связано с энергетическими потерями в системе, возникающими из-за воздействия сил трения или других диссипативных факторов. Чем больше значение декремента затухания, тем быстрее затухают колебания. Определение декремента затухания позволяет оценить устойчивость колебательной системы.
Резонанс — это явление увеличения амплитуды колебаний тела при приложении внешней периодической силы, частота которой равна собственной частоте системы. Это происходит из-за совпадения фазы колебаний тела и внешней силы, что приводит к усилению колебательных процессов. Резонанс может возникать как в механических, так и в электрических системах и играет важную роль во многих технических устройствах и механизмах.
Декремент затухания и резонанс являются важными характеристиками механических колебаний, которые позволяют изучать и анализировать поведение систем во времени. Правильная настройка и управление этими явлениями позволяет повысить эффективность и работоспособность различных технических устройств и механизмов.
Затухающие колебания и остающаяся энергия
Затухающими колебаниями называют такие колебания, при которых амплитуда колебаний уменьшается со временем. Это происходит из-за наличия силы сопротивления, которая постепенно поглощает энергию системы.
При затухающих колебаниях часть энергии превращается в другие формы, такие как тепло или звук. Однако не всю энергию колебательной системы удается полностью поглотить силе сопротивления. Часть энергии остается и продолжает колебаться в системе даже после того, как амплитуда стала незначительной.
Остающаяся энергия в затухающих колебаниях может быть использована для выполнения работы или других полезных действий. Например, в некоторых механизмах остаточные колебания могут использоваться для переключения сигналов или активации других элементов устройства.
Однако в большинстве случаев остающаяся энергия считается нежелательным эффектом и стараются минимизировать его влияние. Для этого применяют различные методы снижения затухания, например, использование материалов с меньшим коэффициентом трения или установка специальных демпфирующих устройств.
Приложения механических колебаний
Механические колебания находят широкое применение в различных областях науки и техники. Они играют важную роль в множестве устройств и технологических процессах. Рассмотрим некоторые из основных приложений механических колебаний.
1. Акустика
Акустика изучает распространение звука и его взаимодействие с веществом. Механические колебания являются основой акустических явлений. Музыкальные инструменты, акустические системы и устройства записи и воспроизведения звука основаны на принципе механических колебаний.
2. Медицина
Механические колебания применяются в медицине для диагностики и лечения различных заболеваний. Например, в УЗИ (ультразвуковая исследовательская диагностика) используются ультразвуковые волны, которые отражаются от внутренних органов и позволяют получить их изображение. Также механические колебания используются в физиотерапии для лечения травм и заболеваний опорно-двигательной системы.
3. Метрология
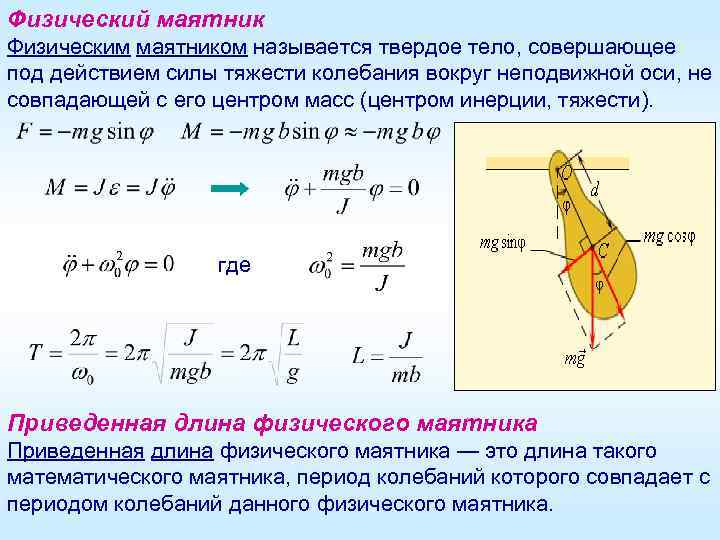
Механические колебания находят применение в метрологии — науке об измерениях. Устройства, основанные на механических колебаниях, позволяют создавать точные измерительные приборы. Например, вибрационные гироскопы используются для определения угловых скоростей и направлений движения. Они применяются в навигационных системах, робототехнике и других отраслях техники.
4. Электроника
Механические колебания используются в электронике для создания таких устройств, как кварцевые резонаторы и генераторы. Кварцевые колебательные контуры используются в часах, радиосвязи, компьютерах и других электронных устройствах для точного измерения времени и генерации стабильных частот.
| Приложение | Примеры |
|---|---|
| Акустика | Музыкальные инструменты, акустические системы, устройства записи и воспроизведения звука |
| Медицина | УЗИ, физиотерапия |
| Метрология | Вибрационные гироскопы, измерительные приборы |
| Электроника | Кварцевые резонаторы, генераторы |
Вопрос-ответ:
Что такое механические колебания?
Механическими колебаниями называют периодическое движение тела вокруг положения равновесия.
Какие могут быть примеры механических колебаний?
Примерами механических колебаний могут служить пульсации сердца, качание качели, колебания струны музыкального инструмента и многое другое.
Какова основная причина возникновения механических колебаний?
Основной причиной возникновения механических колебаний является нарушение равновесия системы, например, под действием внешней силы или энергии.
Как определить амплитуду колебаний?
Амплитуда колебаний определяется как максимальное отклонение объекта от положения равновесия во время колебаний.
Как влияют на параметры механических колебаний масса и жесткость системы?
Масса и жесткость системы оказывают влияние на период и частоту колебаний. Чем больше масса системы, тем меньше период колебаний, а чем больше жесткость системы, тем больше период колебаний.