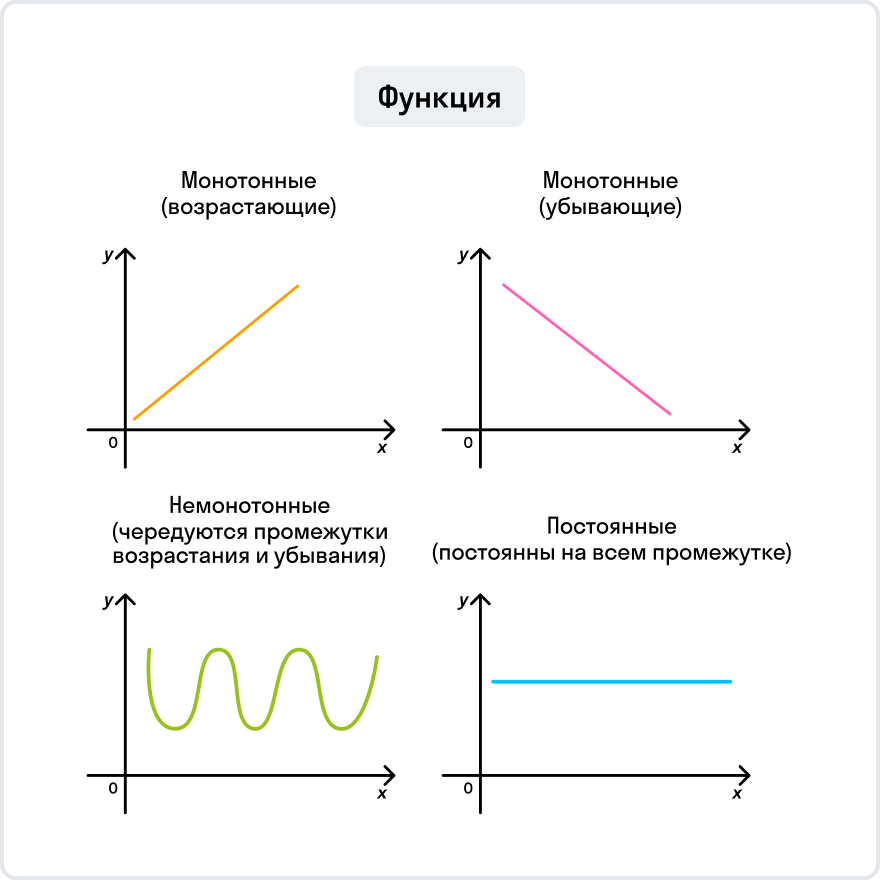
Монотонные функции — это функции, которые сохраняют порядок возрастания или убывания своих значений. Они представляют собой особый класс функций, которые обладают важными свойствами и широко используются в математике, экономике и других науках.
Определение монотонной функции является ключевым шагом для понимания ее поведения и свойств. Чтобы определить, является ли функция монотонной, необходимо учесть ее изменение на промежутке.
Функция является возрастающей монотонной, если ее значения строго возрастают при увеличении аргумента. На графике такая функция будет представлена в виде возрастающей кривой. В то же время, функция считается убывающей монотонной, если ее значения строго убывают при увеличении аргумента. В этом случае, график функции будет представлен в виде убывающей кривой.
Монотонные функции и их определение
Для того чтобы определить, является ли функция монотонной, необходимо проанализировать ее производную. Если производная функции всегда положительна (то есть функция всегда возрастает), то она называется строго возрастающей. Если производная всегда отрицательна (то есть функция всегда убывает), то она называется строго убывающей. Если производная не меняет знака, то функция называется монотонной.
Для наглядности и удобства сравнения значений функции, часто используется таблица, которая показывает значения аргумента и соответствующие значения функции в порядке возрастания (убывания) аргумента. В таблице для монотонных функций можно заметить, что значения функции либо всегда увеличиваются, либо всегда убывают.
| Аргумент (x) | Значение функции (f(x)) |
|---|---|
| x1 | f(x1) |
| x2 | f(x2) |
| x3 | f(x3) |
| x4 | f(x4) |
Таким образом, для определения монотонности функции необходимо проанализировать изменение знака производной и создать таблицу значений аргумента и функции для наглядного представления.
Зачем нужно знать о монотонных функциях?
Понимание и знание монотонных функций полезно в различных областях науки и применяется во многих практических ситуациях. Вот несколько причин, почему полезно знать о монотонных функциях:
- Оптимизация процессов: Монотонные функции могут описывать процессы с постепенным изменением значения. Знание о монотонности функции может помочь в оптимизации различных процессов и систем. Например, в производственных процессах можно использовать монотонные функции для определения оптимальных значений параметров и повышения эффективности.
- Анализ данных: Монотонные функции могут использоваться для анализа данных и статистических моделей. Знание о монотонности функции позволяет строить более точные модели и делать более точные прогнозы. Например, при анализе роста популяции или изменения цен на рынке можно использовать монотонные функции для предсказания будущих тенденций.
- Математическое моделирование: Монотонные функции широко применяются при математическом моделировании различных явлений. Они позволяют описывать различные зависимости и отношения между переменными. Знание о монотонных функциях позволяет более точно моделировать и исследовать различные физические, экономические и социальные процессы.
- Оптимизация алгоритмов: Монотонные функции могут быть полезны при оптимизации алгоритмов и поиске оптимальных решений. Знание о монотонности функций позволяет применять различные методы оптимизации и упрощает решение сложных задач. Например, в задачах машинного обучения монотонные функции могут быть использованы для оптимизации процесса обучения и улучшения точности моделей.
В итоге, знание о монотонных функциях является важным инструментом для анализа данных, оптимизации процессов, математического моделирования и принятия решений в различных областях науки и практике.
Основные понятия
Другое важное понятие, связанное с монотонными функциями, — это экстремумы функций. Экстремум — это точка, в которой функция достигает максимального (максимум) или минимального (минимум) значения. Если функция монотонно возрастает, то ее минимумом будет значение в самой первой точке области определения, а максимумом — значение в самой последней точке. Если функция монотонно убывает, то минимумом будет значение в самой последней точке, а максимумом — значение в самой первой точке.
Монотонные функции широко используются в различных областях математики, физики и экономики. Они позволяют описывать и анализировать процессы, которые увеличиваются или уменьшаются со временем или с изменением других факторов. Знание и понимание монотонных функций полезно при решении задач оптимизации, моделировании и прогнозировании различных явлений.
Примеры монотонных функций
Вот некоторые примеры монотонных функций:
- Линейная функция y = mx + b, где m и b — константы. Если m > 0, то функция является возрастающей. Если m < 0, то функция является убывающей.
- Экспоненциальная функция y = a^x, где a > 1. Эта функция всегда возрастает.
- Логарифмическая функция y = logₐ(x), где a > 1. Эта функция также всегда возрастает.
- Степенная функция y = x^n, где n — целое число. Если n четное и положительное, то функция возрастает. Если n четное и отрицательное, то функция убывает.
- Квадратичная функция y = ax^2 + bx + c, где a > 0. Если a > 0, то функция либо всегда возрастает, либо всегда убывает, в зависимости от знака коэффициента b.
Это только некоторые примеры монотонных функций. Существуют и другие функции, которые также могут быть монотонными.
Определение монотонных функций
Функция называется монотонно возрастающей, если с ростом аргумента значение функции также увеличивается. Например, f(x) = x — монотонно возрастающая функция, так как при увеличении x значение функции также увеличивается.
Функция называется монотонно убывающей, если с ростом аргумента значение функции уменьшается. Например, f(x) = -x — монотонно убывающая функция, так как при увеличении x значение функции уменьшается.
Монотонные функции являются важным объектом изучения в математике, так как они позволяют анализировать и предсказывать изменение различных физических и экономических величин. Например, с помощью монотонных функций можно моделировать зависимость продаж от цены товара или изменение температуры от времени.
Монотонные функции в математике
Функция может быть называться монотонно возрастающей, если значения функции увеличиваются с ростом аргумента. Например, функция f(x) = x^2 является монотонно возрастающей, так как ее значения увеличиваются с увеличением значения аргумента x.
С другой стороны, функция может быть монотонно убывающей, если значения функции убывают при увеличении аргумента. Примером такой функции может быть g(x) = -x, где значения функции уменьшаются с увеличением значения аргумента x.
Монотонные функции могут быть классифицированы на строгие и нестрогие. Монотонно возрастающая функция называется строго возрастающей, если значения функции строго увеличиваются с ростом аргумента. Аналогично, монотонно убывающая функция называется строго убывающей, если значения функции строго уменьшаются при увеличении аргумента.
Определить, является ли функция монотонной, можно с помощью математических методов, таких как дифференцирование или анализ производных. Если производная функции всегда неотрицательна (или всегда неположительна), то функция является монотонно возрастающей (или монотонно убывающей). Если производная функции всегда равна нулю, то функция может быть монотонной на интервалах между точками экстремума.
Монотонные функции играют важную роль в математическом анализе и приложениях. Они используются для описания многочисленных явлений, включая физические, экономические и социальные процессы. Понимание их свойств и характеристик помогает в изучении и анализе различных математических моделей и явлений.
Структура монотонных функций
Структура монотонных функций определяется их основными характеристиками:
- Тип монотонности: монотонные функции могут быть возрастающими или убывающими. Возрастающие функции увеличиваются с каждым значением аргумента, тогда как убывающие функции уменьшаются с ростом аргумента.
- Область определения: это множество всех возможных значений аргумента функции. Область определения может быть конечной или бесконечной.
- Область значений: это множество всех возможных значений функции. Область значений может быть конечной или бесконечной.
- Точки монотонности: это точки, в которых функция меняет свой тип монотонности. Например, точка, в которой возрастающая функция становится убывающей или наоборот.
- Экстремумы: это точки, в которых функция достигает максимального или минимального значения. Возрастающие функции имеют минимумы, убывающие функции имеют максимумы.
Понимание структуры монотонных функций позволяет анализировать их свойства и использовать их в решении задач. Например, знание экстремумов функции может помочь определить ее максимальное или минимальное значение в заданной области. Точки монотонности могут указывать на изменение тренда функции и помочь в прогнозировании ее значения в будущем.
Как определить монотонность функции?
Для определения монотонности функции необходимо проанализировать ее производную. Производная функции показывает скорость изменения функции в каждой точке.
Если производная положительна на всем интервале значений функции, то функция является возрастающей (строго возрастающей). Если производная отрицательна на всем интервале, то функция является убывающей (строго убывающей).
Для определения монотонности функции, нужно взять ее производную и проанализировать знак производной на интервале значений функции.
Если производная равна нулю в точке, то это может означать, что функция имеет экстремум (максимум или минимум) в этой точке. В таком случае, нужно проанализировать знак производной слева и справа от этой точки, чтобы определить, является ли функция возрастающей или убывающей в окрестности точки экстремума.
Если производная функции не меняет знак на интервале, то это может означать, что функция является постоянной (она не возрастает и не убывает).
Анализ производной позволяет определить монотонность функции и понять, как она меняется на протяжении своего определенного интервала значений.
Методы анализа монотонности
Для определения монотонности функции существуют различные методы анализа. В этом разделе рассмотрим основные из них.
1. Метод первой производной: Для функции f(x) необходимо найти ее производную f'(x). Если производная положительна на всем промежутке, то функция возрастает. Если производная отрицательна на всем промежутке, то функция убывает. Если производная равна нулю на всем промежутке, то функция имеет горизонтальный асимптоту.
2. Метод второй производной: Для функции f(x) необходимо найти ее производные f'(x) и f»(x). Если вторая производная положительна на всем промежутке, то функция выпукла вверх. Если вторая производная отрицательна на всем промежутке, то функция выпукла вниз. Если вторая производная равна нулю на всем промежутке, то функция имеет точку перегиба.
3. Метод интервалов: С использованием метода интервалов необходимо выбрать некоторое значение x0 в области определения функции. Затем берется какое-либо значение x1, большее x0. Если f(x1) > f(x0), то функция возрастает на интервале (x0, x1). Если f(x1) < f(x0), то функция убывает на интервале (x0, x1). Если f(x1) = f(x0), то функция сохраняет свою монотонность на интервале (x0, x1).
4. Метод таблиц: Для анализа монотонности функции можно также использовать таблицу значений. Для этого необходимо выбрать некоторое количество значений аргументов и вычислить соответствующие им значения функции. Затем значения функции сравниваются в порядке возрастания или убывания аргументов. Если значения возрастают, то функция возрастает. Если значения убывают, то функция убывает. Если значения функции не изменяются, то функция сохраняет свою монотонность.
Примечание: При использовании данных методов необходимо учитывать область определения функции и пределы, если они существуют.
Вопрос-ответ:
Как определить, является ли функция монотонной?
Функция называется монотонно возрастающей, если при увеличении значения аргумента, значение функции также увеличивается. Аналогично, функция называется монотонно убывающей, если при увеличении значения аргумента, значение функции уменьшается. Чтобы определить, является ли функция монотонной, необходимо анализировать изменение значения функции при увеличении аргумента в заданном интервале.
Как выразить определение монотонной функции математическим языком?
Функция f(x) называется монотонно возрастающей на интервале (a, b), если для любых двух точек x1 и x2 в этом интервале, таких что x1 < x2, значение функции f(x1) меньше значения f(x2). Аналогично, функция f(x) называется монотонно убывающей на интервале (a, b), если для любых двух точек x1 и x2 в этом интервале, таких что x1 < x2, значение функции f(x1) больше значения f(x2).
Какими способами можно определить монотонность функции графически?
Существует несколько способов определить монотонность функции графически. Один из них — по форме графика функции. Если график функции строго возрастает при увеличении аргумента на всем заданном интервале, то функция является монотонно возрастающей на этом интервале. Если график функции строго убывает при увеличении аргумента на всем заданном интервале, то функция является монотонно убывающей на этом интервале.
Какие есть условия для определения монотонности функции?
Для определения монотонности функции, необходимо выполнять одно из двух условий. Для монотонно возрастающей функции, значения функции при увеличении аргумента должны также увеличиваться. Для монотонно убывающей функции, значения функции при увеличении аргумента должны уменьшаться. Если одно из этих условий выполняется, то функция является монотонной на заданном интервале.
Могут ли функции быть одновременно монотонно возрастающими и убывающими?
Нет, функция не может быть одновременно монотонно возрастающей и убывающей на одном и том же интервале. Если функция строго возрастает на каком-то интервале, она не может строго убывать на этом интервале и наоборот. Однако, функция может быть монотонной на разных интервалах.
Что такое монотонные функции?
Монотонные функции — это функции, которые либо всегда возрастают, либо всегда убывают на всей области определения.
Как определить, является ли функция монотонной?
Для определения монотонности функции нужно проанализировать ее производную. Если производная всегда положительна на всей области определения, то функция является возрастающей. Если производная всегда отрицательна, то функция является убывающей.