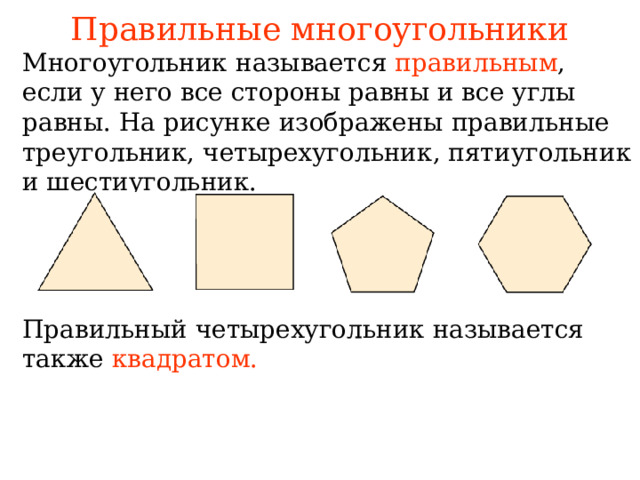
Многоугольники – это фигуры, состоящие из нескольких отрезков, называемых сторонами. Однако не все многоугольники одинаковы. В зависимости от количества сторон и их длин, многоугольники могут быть разнообразными. Исключением являются правильные многоугольники.
Правильные многоугольники – это особый вид фигур, у которых все стороны равны друг другу. Таким образом, каждый угол правильного многоугольника также будет равен. Это свойство придает им симметричность и гармоничность внешнего вида.
Известные примеры правильных многоугольников – это треугольник, квадрат, пятиугольник, шестиугольник, семиугольник, восьмиугольник и так далее. Отличительной особенностью этих фигур является равенство всех сторон. Благодаря этому свойству правильные многоугольники широко используются в геометрии, строительстве и других научных и практических областях.
Определение правильного многоугольника
Правильным называется многоугольник, у которого все стороны равны между собой и все углы равны. Такой многоугольник считается особым и имеет некоторые интересные свойства и характеристики.
Критерии правильного многоугольника
Для того чтобы определить, является ли данный многоугольник правильным, необходимо проверить два основных критерия:
- Все стороны равны. Это значит, что длина каждой стороны многоугольника должна быть одинаковой. Неравные стороны делают многоугольник неправильным.
- Все углы равны. У каждого угла многоугольника мера должна быть одинаковая. Углы разной величины делают многоугольник неправильным.
Если оба критерия выполняются, то многоугольник считается правильным.
Примеры правильных многоугольников

Примерами правильных многоугольников являются:
- Равносторонний треугольник: у него все стороны равны и все углы равны 60 градусов.
- Равносторонний четырехугольник (квадрат): у него все стороны равны и все углы равны 90 градусов.
- Равносторонний пятиугольник (пентагон): у него все стороны равны и все углы равны 108 градусов.
- И т.д.
Правильные многоугольники встречаются не только в математике, но и в природе, например, в кристаллах или шестиугольных сотах пчел. Они также используются в строительстве и дизайне, благодаря своей симметрии и гармонии.
Основные характеристики прямоугольного многоугольника
Основные характеристики прямоугольного многоугольника включают:
- Углы: Прямые углы являются главной характеристикой прямоугольного многоугольника. Они составляют 90 градусов и расположены в каждой вершине многоугольника.
- Стороны: Прямоугольный многоугольник имеет равные стороны, что отличает его от произвольного многоугольника. Каждая сторона соединяет две соседние вершины, и все они имеют одинаковую длину.
- Диагонали: Диагонали прямоугольного многоугольника — это линии, соединяющие не смежные вершины. В прямоугольном многоугольнике с каждой вершиной проведены две диагонали, и они образуют прямые углы с каждой стороной многоугольника.
- Периметр: Периметр прямоугольного многоугольника вычисляется как сумма длин всех его сторон. Из-за равенства сторон в прямоугольном многоугольнике, его периметр можно выразить как произведение длины одной из сторон на количество сторон.
- Площадь: Площадь прямоугольного многоугольника вычисляется как произведение длины одной из сторон на высоту, опущенную к этой стороне. Также площадь можно выразить как произведение длин двух диагоналей, деленное на 2.
Важно отметить, что прямоугольный многоугольник является специальным случаем многоугольника. Все его свойства и характеристики основаны на равенстве углов и сторон. Изучение прямоугольных многоугольников помогает в понимании и решении геометрических задач, а также применяется в различных отраслях науки и техники.
Условия равности всех сторон многоугольника
Многоугольник называется правильным, если все его стороны равны друг другу. Это означает, что у такого многоугольника каждая сторона имеет одинаковую длину.
Чтобы определить, является ли многоугольник правильным, необходимо измерить длину каждой стороны и сравнить их значения. Если все стороны равны, то многоугольник может считаться правильным.
Равные стороны многоугольника придают ему симметрию и структуру. Правильные многоугольники часто встречаются в геометрии и имеют свои особенности, связанные с равенством и углами.
Существуют различные виды правильных многоугольников, включая треугольник, квадрат, пятиугольник (пентагон), шестиугольник (гексагон), семиугольник (гептагон) и т.д. Каждый из них обладает своими уникальными свойствами и особенностями конструкции.
Знание условий равности всех сторон многоугольника позволяет классифицировать его и более глубоко изучать его свойства и характеристики. Это является важным инструментом в геометрии для понимания и решения различных задач.
Свойства правильного многоугольника
Основные свойства правильного многоугольника:
1. Равные стороны
В правильном многоугольнике все стороны имеют одинаковую длину. Это позволяет ему иметь симметричную форму и выглядеть гармонично.
2. Равные углы
Все углы между сторонами правильного многоугольника также имеют одинаковую меру. Это предоставляет многоугольнику симметричность и равномерность.
Важно знать, что количество сторон правильного многоугольника определяется формулой: n = 360° / α, где n — количество сторон, α — мера одного угла.
Правильные многоугольники часто встречаются в геометрии и имеют много применений, включая в архитектуре, макетировании и создании графических фигур.
Как определить, является ли многоугольник правильным?

Шаг 1: Проверка равенства всех сторон
Первым шагом необходимо измерить каждую сторону многоугольника и убедиться, что все они равны между собой. Можно использовать линейку или другой специальный инструмент для измерения длин сторон.
Шаг 2: Проверка равенства всех углов
Вторым шагом необходимо проверить равенство всех углов многоугольника. Если многоугольник является многоугольником равносторонним, то все его углы также будут равными. Для этого можно использовать гониометр или другой инструмент для измерения углов.
Примечание: Правильный многоугольник обычно имеет дополнительные свойства, такие как равность всех его диагоналей и площадей подмногоугольников, но для определения его правильности достаточно проверить равенство сторон и углов.
Примеры правильных многоугольников
Одним из примеров правильных многоугольников является треугольник. В правильном треугольнике все стороны имеют одинаковую длину, а углы равны 60 градусов.
Еще одним примером правильного многоугольника является квадрат. У квадрата все стороны равны, а углы равны 90 градусов.
Другим примером правильного многоугольника является пятиугольник, или пентагон. У пятиугольника все стороны равны, а углы равны 108 градусов.
Шестиугольник, или гексагон, также является правильным многоугольником. У него все стороны и углы равны.
Восьмиугольник, или октагон, также относится к классу правильных многоугольников. У него все стороны равны, а углы равны 135 градусов.
Десятиугольник, или декагон, также может быть правильным, если у него все стороны равны и углы равны 144 градуса.
Это лишь некоторые примеры правильных многоугольников. В реальности их может быть бесконечное количество, с разным числом сторон и углов.
Отличия правильных многоугольников от неправильных
Неправильный многоугольник — это многоугольник, у которого не все стороны или углы равны.
Знаки правильных многоугольников:
- Все стороны правильного многоугольника имеют одинаковую длину.
- Все углы правильного многоугольника равны.
- Правильные многоугольники обладают симметрией относительно центральной точки (центра).
Отличия неправильных многоугольников:
- У неправильного многоугольника могут быть стороны разной длины.
- У неправильного многоугольника могут быть различные углы.
- У неправильного многоугольника отсутствует симметрия относительно центральной точки.
Использование правильных многоугольников в геометрии и в повседневной жизни
Одно из наиболее известных применений правильных многоугольников связано с построением и измерением. Благодаря своей симметрии и точно определенным углам и сторонам, правильные многоугольники можно использовать для построения геометрических фигур и измерения расстояний и углов. Например, правильный треугольник может использоваться для построения прямоугольника или квадрата, а правильный пятиугольник может быть использован для измерения угла между двумя линиями.
Помимо геометрии, правильные многоугольники находят применение в архитектуре и дизайне. Их симметричная форма и выразительный вид делают их привлекательными для использования в архитектурных элементах, фасадах зданий и декоративных элементах интерьера. Например, правильные шестиугольники могут быть использованы для создания красивых мозаичных паттернов или для построения геометрических узоров на стенах.
Правильные многоугольники также широко применяются в науке и технике. Они используются для моделирования молекул, кристаллических структур и других сложных объектов. Их точная геометрия позволяет исследователям более глубоко понять и описать трехмерную структуру различных объектов. Кроме того, правильные многоугольники используются в строительстве, где они могут быть использованы для создания устойчивых и эффективных конструкций, таких как арки или купола.
В повседневной жизни правильные многоугольники также находят свое применение. Они используются в дизайне украшений, логотипов компаний, упаковке продуктов и даже в играх. Кроме того, правильные многоугольники могут использоваться для развития логического мышления, математических навыков и умения работать с абстрактными понятиями.
Таким образом, использование правильных многоугольников в геометрии и в повседневной жизни имеет широкий спектр применений. Они помогают в построении, измерении, моделировании и дизайне, а также способствуют развитию креативности и аналитического мышления. Изучение и использование этих геометрических фигур могут быть полезными для широкого круга людей, независимо от их профессии или уровня образования.
Вопрос-ответ:
Что такое многоугольник?
Многоугольник — это фигура, которая образуется при соединении нескольких отрезков (сторон), таким образом, что каждая сторона пересекается только с двумя другими сторонами, а конечные точки сторон не совпадают.
Когда многоугольник называется правильным?
Многоугольник называется правильным, если у него все стороны равны и все углы равны.
Какие особенности у правильного многоугольника?
Особенностью правильного многоугольника является равенство всех его сторон и всех его углов. Также у правильного многоугольника центральные углы будут равными и радиус описанной окружности будет одинаковым для всех его сторон.
Что означает равенство углов и сторон в правильном многоугольнике?
Равенство углов в правильном многоугольнике означает, что все углы многоугольника равны между собой. Равенство сторон означает, что все стороны многоугольника имеют одинаковую длину.
Какие примеры можно привести правильных многоугольников?
Примерами правильных многоугольников являются равносторонний треугольник, квадрат, правильный пятиугольник (пентагон), правильный шестиугольник (гексагон), правильный семиугольник (гептагон) и т.д.
Что такое правильный многоугольник?
Правильный многоугольник — это многоугольник, у которого все стороны и все углы равны между собой.