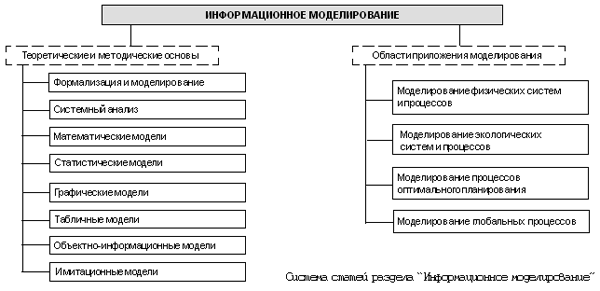
Современный мир полон разнообразных сложных систем: от экономики и финансов до климата и коллективного поведения людей. Изучение этих систем и понимание их динамики – задача непростая. Один из способов приблизиться к их моделированию – это использование случайных элементов в поведении системы.
Моделирование сложных систем с элементами случайности подразумевает создание математических моделей, которые учитывают стохастические факторы и позволяют предсказывать и анализировать поведение системы в разных условиях и сценариях.
Такие модели имеют огромное практическое применение в самых различных областях, начиная от финансовых рынков и прогнозирования погоды, заканчивая сетевыми коммуникациями и социальными сетями. Модели со случайными составляющими помогают прогнозировать изменения, изучать и предсказывать поведение системы, а также оценивать вероятности различных сценариев.
Таким образом, модели сложных систем с элементами случайности становятся необходимым инструментом для тех, кто стремится лучше понять и оценить динамику и характеристики таких систем. С их помощью мы можем разработать более эффективные стратегии принятия решений, а также прогнозировать возможные последствия воздействия на эти системы.
Принципы моделирования сложных систем
Принципы моделирования сложных систем включают:
1. Иерархический подход
Для успешного моделирования сложных систем необходимо разбивать их на более мелкие подсистемы или компоненты. Используя иерархическую структуру, мы можем лучше понять взаимосвязи между элементами системы и управлять ими.
2. Статистический анализ
Поведение сложных систем часто обусловлено случайными факторами. Важно учитывать статистические закономерности в поведении компонентов системы, чтобы предсказать их влияние на систему в целом. Моделирование статистических свойств и проведение статистического анализа позволяют более точно прогнозировать работу системы.
3. Учет динамических процессов
Сложные системы часто подвержены изменению со временем. Необходимо учитывать и моделировать эти динамические процессы, чтобы понять и предсказать будущее поведение системы. Моделирование динамических процессов позволяет анализировать как краткосрочные, так и долгосрочные изменения в системе.
Использование этих принципов позволяет более точно и полно описать поведение сложных систем с элементами случайности и предсказывать их будущую работу. Моделирование сложных систем является важным инструментом для различных областей, таких как экономика, физика, социология и технические науки.
| Принципы моделирования сложных систем |
|---|
| Иерархический подход |
| Статистический анализ |
| Учет динамических процессов |
Абстракция и упрощение
Абстрагирование позволяет сфокусироваться на ключевых аспектах системы, исключив ненужную информацию, и упростить понимание ее работы. При создании моделей сложных систем с элементами случайного поведения необходимо выбрать те аспекты, которые наиболее важны для достижения цели моделирования, и опустить меньшую важность.
Преимущества абстракции и упрощения
- Увеличение визуальной четкости и понятности модели.
- Сокращение объема информации, что делает модель более доступной для анализа и интерпретации.
- Ускорение процесса моделирования и анализа системы.
- Способствует обнаружению общих закономерностей и принципов работы системы.
Системный подход
Основной идеей системного подхода является понимание, что система может быть рассмотрена как набор взаимосвязанных элементов, которые взаимодействуют друг с другом в определенном окружении. При этом поведение системы определяется не только свойствами ее отдельных элементов, но и их взаимодействиями и влияниями на окружающую среду.
Основные принципы системного подхода:
- Выделение системы как объекта исследования;
- Учет взаимосвязей и взаимодействий между компонентами системы;
- Учет динамической природы системы и возможности изменения ее состояния;
- Анализ системы в контексте ее окружения;
- Учет случайности и стохастичности в поведении системы.
Системный подход позволяет рассмотреть систему в целом, представляя ее как сложное динамическое образование. При анализе системы с элементами поведения, которые может быть случайным, системный подход помогает учесть случайность и стохастичность в ее моделировании и прогнозировании.
Взаимодействие компонентов
В моделях сложных систем с элементами поведения, которые могут быть случайными, взаимодействие компонентов играет ключевую роль. Компоненты таких систем взаимодействуют между собой, обмениваются информацией и влияют на свое окружение.
Взаимодействие между компонентами может происходить различными способами. Оно может быть направленным или ненаправленным, синхронным или асинхронным. Также взаимодействие может быть детерминированным или случайным.
Одним из способов взаимодействия компонентов является передача сообщений. Компоненты могут обмениваться сообщениями, содержащими информацию об их текущем состоянии или требующими выполнения определенного действия. Этот способ взаимодействия часто применяется в агентных моделях, где каждый компонент является автономным агентом, обладающим своей логикой поведения.
Еще одним способом взаимодействия является сетевое взаимодействие. Компоненты системы могут взаимодействовать через сеть, отправляя и принимая данные по определенному протоколу. Это позволяет компонентам располагаться на разных узлах сети и обмениваться информацией даже в удаленном режиме.
Случайные элементы в поведении компонентов могут оказывать влияние на взаимодействие. Вероятность возникновения определенного взаимодействия или приоритет определенных действий может быть случайной. Это позволяет моделировать неточности и случайности, которые характерны для реальных систем.
Пример взаимодействия компонентов:
- Компонент A генерирует случайные данные и передает их компоненту B.
- Компонент B обрабатывает полученные данные и принимает решение на основе случайного фактора.
- Компонент B передает результат своего решения компоненту C.
- Компонент C принимает решение на основе полученных данных и случайного фактора и передает результат компоненту D.
Взаимодействие компонентов в моделях сложных систем с элементами случайности позволяет обеспечить более реалистичное моделирование и анализ систем, которые имеют периодическое или непредсказуемое поведение.
Управление случайным поведением
Для управления случайным поведением могут использоваться различные методы и подходы. Один из них — статистическое управление случайными процессами. Оно основано на математическом анализе и предоставляет возможность оптимизировать характеристики системы при наличии случайных факторов.
Еще одним подходом к управлению случайным поведением являются методы машинного обучения. Они позволяют создавать модели и алгоритмы, которые обучаются на основе исторических данных и предсказывают поведение системы в будущем.
Разработка алгоритмов управления случайным поведением требует комплексного подхода и включает в себя анализ данных, определение целевых функций и выбор оптимальных стратегий управления. Кроме того, необходимо учитывать риски и вероятности различных событий, связанных с случайностью поведения системы.
Важным аспектом управления случайным поведением является способность адаптироваться к изменяющимся условиям и принимать решения в режиме реального времени. Для этого могут быть применены методы адаптивного управления, которые позволяют системе изменять свое поведение в зависимости от текущих обстоятельств.
Управление случайным поведением имеет широкое применение в различных областях, таких как финансы, производство, транспорт, энергетика и другие. Оно помогает обеспечивать стабильность и надежность работы систем, улучшать их эффективность и снижать риски при наличии случайных факторов.
Итеративное моделирование
Итеративное моделирование является одним из основных подходов к разработке и исследованию сложных систем. Оно позволяет учитывать случайность и неопределенность в поведении элементов системы и помогает прогнозировать и анализировать их влияние на общую динамику системы.
В процессе итеративного моделирования создается итеративная модель, которая представляет собой последовательность состояний системы и переходов между этими состояниями. Каждая итерация моделирования представляет собой шаг, в ходе которого система переходит из одного состояния в другое с учетом случайного воздействия на элементы системы.
Итеративное моделирование позволяет анализировать различные сценарии развития системы, связанные с разной степенью случайности и неопределенности. Это позволяет исследовать различные варианты работы системы, предвидеть возможные риски и принимать соответствующие меры для их устранения или снижения.
Итеративное моделирование является мощным инструментом в различных областях, таких как экономика, финансы, биология, социология и т. д. Оно помогает понять и предсказать сложное поведение системы, в которой взаимодействуют многочисленные случайные факторы.
Валидация и верификация моделей
Верификация моделей, с другой стороны, заключается в проверке достоверности и точности модели. Целью верификации является определение соответствия модели собственным объектам или свойствам исследования. Верификация включает в себя проверку адекватности модели и ее соответствия необходимым условиям и требованиям.
Методы валидации и верификации моделей
Для валидации и верификации моделей существует несколько методов, которые могут быть применены в зависимости от конкретной задачи. Один из таких методов — использование количественных и качественных данных для проверки модели на соответствие реальной системе. Другие методы включают математические аналитические методы, статистические тесты и симуляции моделей.
Кроме того, валидация и верификация моделей включает также проверку на случайность и стохастичность поведения модели. Для этого могут применяться различные статистические методы и тесты случайности. Это позволяет убедиться в корректности и достоверности модели при случайных событиях и состояниях.
Значимость валидации и верификации моделей
Валидация и верификация моделей играют важную роль в различных областях, включая науку, инженерию, экономику и другие сферы. Корректность и достоверность моделей являются ключевыми аспектами для принятия правильных решений, проведения исследований и оптимизации процессов.
Прогнозирование и анализ результатов
Прогнозирование
Прогнозирование результатов модели сложной системы позволяет предсказать ее поведение в будущем. В основе прогнозирования лежат математические модели, которые учитывают случайность и неопределенность в поведении системы.
Одним из методов прогнозирования является статистическое моделирование, которое основано на анализе статистических свойств исходных данных и построении моделей, которые позволяют предсказывать будущие значения системы.
Анализ результатов
Анализ результатов моделирования сложных систем помогает оценить достоверность, точность и полноту полученных прогнозов. В процессе анализа рассматриваются различные факторы, влияющие на поведение системы, и проводится их оценка.
Также важным аспектом анализа результатов является выявление факторов, которые могут вызывать неопределенность и случайность в поведении системы. Это позволяет лучше понять, какие факторы могут быть определены и контролируемыми, а какие – нет.
Примеры моделей сложных систем
Модели сложных систем с элементами случайного поведения широко применяются в различных областях науки и техники. Вот несколько примеров таких моделей:
1. Модель случайного блуждания
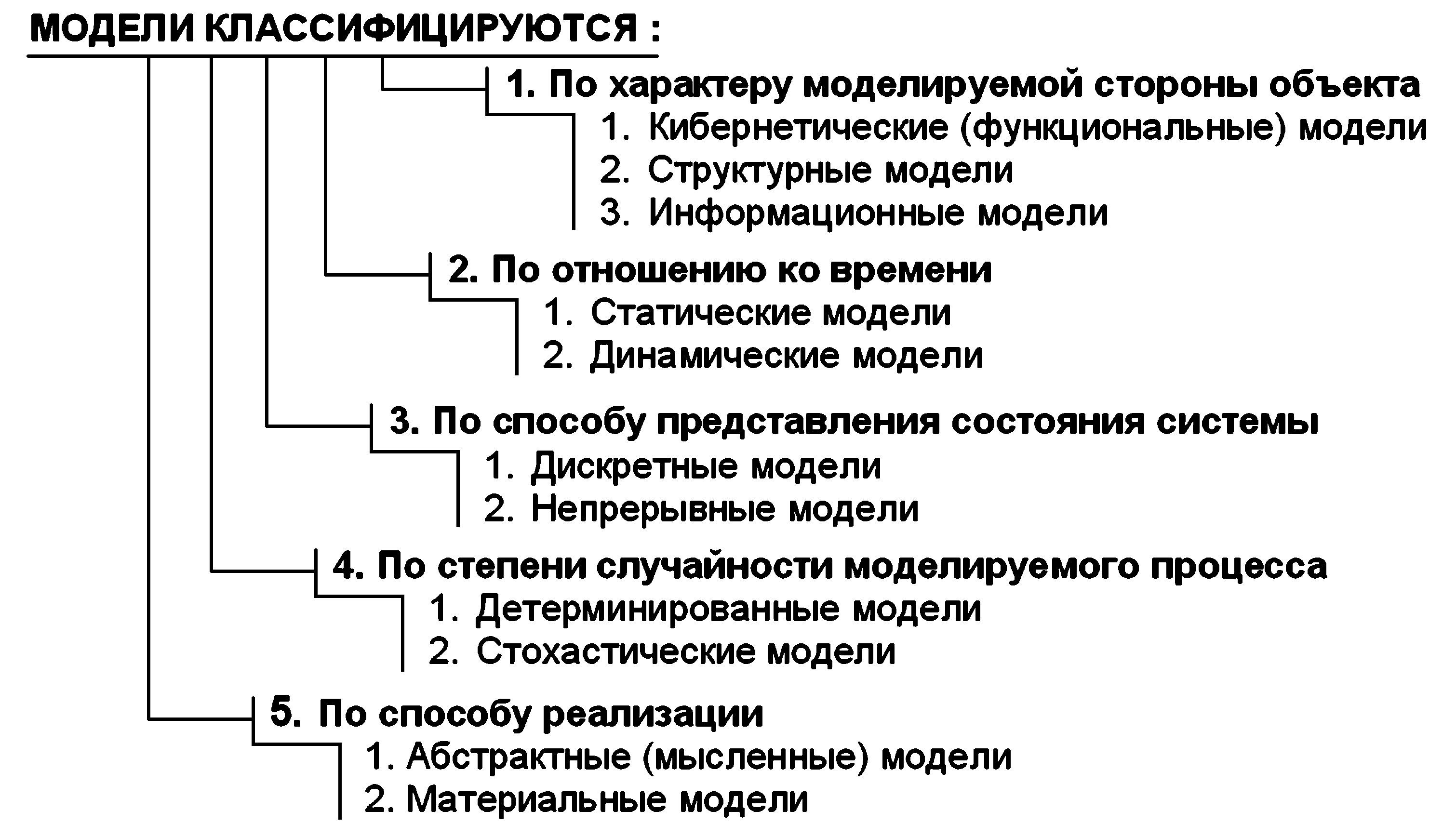
Модель случайного блуждания используется для описания движения частицы, которая на каждом шаге делает случайный переход из текущего состояния в соседнее состояние. Эта модель находит применение в физике, финансовой математике, компьютерной графике и других областях.
2. Модель случайного графа
Модель случайного графа позволяет описывать различные сетевые структуры, такие как социальные сети, интернет и транспортные сети. В данной модели вершины и ребра графа генерируются случайным образом в соответствии с определенными правилами.
3. Модель случайного процесса
Модель случайного процесса используется для описания эволюции системы во времени, когда ее поведение зависит от случайных факторов. Такие модели применяются в экономике, погоде, телекоммуникациях и других областях, где важно учесть возможность появления случайных событий.
Приведенные примеры являются лишь небольшой частью многообразия моделей сложных систем, в которых присутствуют случайные элементы. Эти модели помогают понять и предсказать поведение реальных систем и применяются в различных научно-исследовательских и инженерных задачах.
Модель экономической системы
В такой модели учитываются не только основные экономические агенты — потребители, производители и государство, но и различные факторы, влияющие на экономические процессы.
Модель экономической системы отражает взаимосвязи и зависимости между различными элементами и переменными, такими как производство, труд, капитал, инновации, цены, доходы и потребление.
Экономическая модель может быть разработана для анализа и прогнозирования поведения экономических агентов, оценки влияния изменений в экономических условиях и принятия решений по оптимизации экономических процессов.
При разработке моделей экономических систем используются различные методы и подходы, такие как математическое моделирование, статистический анализ, эконометрика и теория игр.
Вопрос-ответ:
Какие системы называются моделями сложных систем с элементами поведения которых может быть случайным?
Моделями сложных систем с элементами поведения, которые может быть случайным, называются стохастические модели.
Что означает понятие «сложная система»?
Сложная система — это система, состоящая из множества взаимодействующих компонентов, обладающих сложной структурой. Такая система характеризуется тем, что поведение всей системы не может быть предсказано путем анализа поведения отдельных компонентов.
Какие примеры сложных систем с элементами поведения, которые может быть случайным, существуют?
Примерами сложных систем с элементами поведения, которые может быть случайным, являются финансовые рынки, погодные системы, общественные сети, биологические системы и т.д.
Каким образом моделируются сложные системы с элементами поведения, которые может быть случайным?
Для моделирования сложных систем с элементами поведения, которые может быть случайным, часто используются стохастические процессы, математический аппарат теории вероятностей и статистики. Это позволяет учесть случайность и неопределенность в поведении системы.