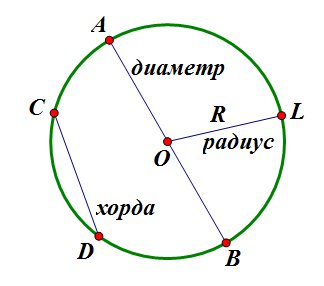
Отрезком называют прямую линию, которая соединяет две точки на окружности. Окружность – это плоская фигура, состоящая из всех точек на плоскости, находящихся на одинаковом расстоянии от центра. Соединение двух точек окружности отрезком является одним из основных понятий геометрии.
Отрезки, соединяющие две точки окружности, имеют важное значение в геометрии. Они позволяют определить различные характеристики окружности, такие как длина окружности, диаметр, радиус, и многое другое. Кроме того, отрезки окружности используются для решения различных задач, связанных с геометрией, например, для нахождения точек пересечения окружностей.
Важно отметить, что отрезок, соединяющий две точки окружности, может быть как прямым, так и кривым. Например, если две точки находятся на разных радиусах окружности, отрезок окажется радиусом. Если же точки находятся на одном радиусе, отрезок будет выглядеть как дуга окружности.
Что такое отрезок?
Отрезок может быть прямым или кривым, горизонтальным или вертикальным, коротким или длинным. В контексте окружностей, отрезок соединяющий две точки на окружности называется хордой. Хорда является простым и удобным способом соединения двух точек на окружности, и она играет важную роль в решении различных задач, связанных с окружностями.
Отрезки могут быть измерены с помощью различных единиц измерения, таких как дюймы, сантиметры или метры. Длина отрезка может быть вычислена с использованием формулы, учитывающей расстояние между двумя точками и их координаты. Отрезки являются основным элементом в геометрии, и их изучение является важной частью математического образования.
Определение отрезка
Отрезок соединяет две точки окружности, к которым он принадлежит. Он представляет собой кратчайшую длину между этими точками и обладает свойствами, которые можно использовать в геометрических расчетах и задачах.
Отрезок может быть задан различными способами, например, через координаты его концов или через длину и положение на координатной плоскости. Он может быть прямым или кривым, горизонтальным или вертикальным.
В отрезке можно выделить его длину, которая равна расстоянию между его началом и концом. Отрезок также имеет направление, определяемое порядком следования его концов.
Отрезок как геометрическая фигура
Отрезки могут использоваться для измерения расстояний между точками. Они широко применяются в различных областях, включая математику, физику, геометрию и конструкцию.
Отрезки могут быть прямыми или кривыми, в зависимости от их формы и положения точек, которые они соединяют. В геометрии отрезки часто обозначаются двумя точками, которые находятся на их концах.
Отрезки имеют свойства, которые могут быть использованы для определения их свойств, таких как длина, направление, ориентация и положение в пространстве.
Отрезок, соединяющий две точки на окружности, называется хордой. Хорда может быть отрезком длиной, равной или меньше диаметра окружности.
Математическое определение отрезка
Отрезок может быть определен как участок прямой между двумя точками окружности. Он также может быть определен как минимальное расстояние между двумя точками. В математике отрезок обычно обозначается двумя точками, находящимися на его концах, например, AB.
Отрезок может быть описан с помощью его длины, которая измеряется в единицах измерения длины, и его направления, которое определяется положением точек окружности.
Отрезок может быть использован для моделирования различных объектов в геометрии и физике, таких как линии, отрезки времени или связей между двумя точками. Он также является основным элементом в построении геометрических фигур и решении задач, связанных с расстояниями и отношениями.
Свойства отрезка
Отрезок, соединяющий две точки окружности, обладает рядом интересных свойств:
- Длина отрезка равна разности длин дуг, которые он вырезает на окружностях.
- В случае, когда окружности не пересекаются, длина отрезка является кратчайшим расстоянием между точками на окружностях.
Отрезок также может иметь следующие свойства:
- Прямой отрезок: все точки отрезка лежат на прямой.
- Замкнутый отрезок: начальная и конечная точки отрезка совпадают.
- Открытый отрезок: начальная и конечная точки отрезка не совпадают.
- Сегмент отрезка: отрезок вместе со своими начальной и конечной точками.
Эти свойства отрезка играют важную роль в геометрии и находят свое применение в решении различных задач, связанных с окружностями.
Отрезок имеет конец
Концы отрезка называются концами отрезка. Они являются точками, в которых отрезок заканчивается и начинается. Каждый отрезок имеет два конца — начальный и конечный.
В математике обычно используют обозначения для концов отрезка. Начальный конец обычно обозначается буквой A, а конечный конец — буквой B. Таким образом, отрезок обозначается как AB.
Концы отрезка могут быть любыми точками, как внутри окружности, так и за ее пределами. Важно помнить, что отрезок — это только часть прямой линии, которая соединяет две точки, и его концы могут находиться в любом месте.
Отрезок ограничен длиной
Для определения длины отрезка используется формула длины дуги:
| Формула | Краткое описание |
|---|---|
| 𝐿 = 𝑟𝜃 | Длина дуги, где 𝐿 — длина дуги, 𝑟 — радиус окружности, 𝜃 — центральный угол дуги в радианах. |
Таким образом, отрезок между двуми точками окружности имеет ограниченную длину, равную длине дуги, соединяющей эти точки. Определение длины отрезка играет важную роль в геометрии и может быть использовано в различных задачах и рассуждениях.
Применение отрезка в геометрии
Первое применение отрезка — определение расстояния между двумя точками. Когда две точки заданы на плоскости или в пространстве, можно использовать отрезок, соединяющий эти точки, чтобы вычислить расстояние между ними. Данное расстояние может быть вычислено с помощью формулы длины отрезка, которая основывается на координатах этих точек.
Второе применение — построение геометрических фигур. Отрезки часто используются для построения различных фигур, таких как треугольники, прямоугольники, многоугольники и другие. Они могут быть использованы как стороны фигур, а также как диагонали, высоты или медианы.
Третье применение — решение геометрических задач и задач оптимизации. Отрезки используются для решения широкого спектра задач, связанных с геометрией. Например, они могут быть использованы для определения кратчайшего пути между двумя точками, нахождения точки, наиболее удаленной от других точек, определения площади фигуры и многое другое.
| Применение | Пример |
|---|---|
| Расстояние | Отрезок AB имеет длину 5 единиц |
| Построение фигур | Отрезки AB, BC и CA образуют треугольник ABC |
| Задачи оптимизации | Отрезок AC является кратчайшим путем между точками A и C |
Таким образом, отрезок является важным понятием в геометрии и имеет множество применений. Он позволяет решать различные задачи, строить фигуры и определять расстояния между точками.
Вопрос-ответ:
Что такое отрезок, соединяющий две точки окружности?
Отрезок, соединяющий две точки окружности, называется хорда.
Как называется отрезок, соединяющий две точки окружности?
Отрезок, соединяющий две точки окружности, имеет название хорда.
Каково название отрезка, проведенного между двумя точками окружности?
Отрезок, проведенный между двумя точками окружности, называется хордой.
Как называется отрезок, который соединяет две точки окружности?
Отрезок, который соединяет две точки окружности, имеет название хорда.