Математика — это удивительная наука, которая помогает нам понять и описать мир вокруг нас. Одним из важных аспектов математического анализа является изучение геометрии, в которой изучаются фигуры, их свойства и взаимосвязи между ними.
Одна из интересных фигур, которую можно встретить в геометрии, — это фигура, образованная точкой, принадлежащей прямой и одной из ее частей. Эта фигура называется отрезком.
Отрезок — это часть прямой, ограниченная двумя точками, одна из которых принадлежит прямой, а другая — находится вне ее. Иными словами, отрезок — это фигура, состоящая из точек, лежащих на прямой, и точек, лежащих вне нее.
Отрезок является важным понятием в геометрии и имеет свои свойства, которые можно изучать и использовать для решения различных задач. Например, длина отрезка — это величина, которая характеризует размер фигуры и может быть выражена в единицах измерения.
Фигура, образованная точкой на прямой и ее часть
В геометрии существует особенная фигура, которая образуется при помощи точки на прямой и одной из ее частей. Эта фигура называется отрезком.
Отрезок — это фигура, которая состоит из двух конечных точек на прямой и всех точек, которые лежат между этими двумя точками. Конечные точки отрезка обозначаются заглавными буквами.
Отрезки имеют свойства, которые отличают их от других фигур. Один из основных принципов отрезка заключается в том, что он является прямым отрезком между своими конечными точками. Также отрезок можно характеризовать его длиной, которая равна расстоянию между его конечными точками.
Отрезки могут быть использованы для измерения и сравнения других фигур. Например, с помощью отрезков можно измерить длину прямой или сравнить длину двух отрезков.
Важно понимать, что отрезок является одной из основных фигур в геометрии, и его свойства и использование необходимо знать для дальнейшего изучения этой науки.
Определение точки
Точка может быть задана с помощью координат, которые указывают ее положение относительно системы координат. В двумерном пространстве точка имеет две координаты — x и y, обозначающие ее расстояние от начала координат по горизонтальной и вертикальной оси соответственно.
Точка также может находиться на прямой или находиться внутри другой геометрической фигуры, такой как окружность, треугольник или прямоугольник. В этом случае мы можем сказать, что точка принадлежит этой фигуре.
Точки могут быть объединены для создания отрезков, линий, лучей и других геометрических фигур. Они также играют важную роль в математических вычислениях и анализе данных. Определение точки является основой для изучения геометрии и широко применяется в различных областях знаний.
Прямая и ее характеристики
Направление прямой
Направление прямой определяется тем, как она простирается в пространстве. Прямая может быть вертикальной, когда ее направление идет вверх или вниз, или горизонтальной, когда ее направление идет слева направо или справа налево. Кроме того, прямая может быть наклонной, когда ее направление образует угол с горизонтальной или вертикальной осью.
Угол наклона прямой
Угол наклона прямой определяет ее наклон или наклонность относительно горизонтальной или вертикальной оси. Угол наклона измеряется в градусах и может быть положительным или отрицательным. Если угол наклона положителен, то прямая наклонена вверх или справа. Если угол наклона отрицателен, то прямая наклонена вниз или слева.
Прямая — одна из основных фигур в геометрии и ее характеристики позволяют определять ее форму и положение в пространстве. Понимание этих характеристик помогает в изучении геометрии и решении задач, связанных с расположением и взаимодействием прямых.
Фигура, образованная точкой на прямой
Фигура, образованная точкой на прямой представляет собой геометрическую структуру, которая возникает в результате рассмотрения точки на прямой и одной из ее окружающих частей.
Точка на прямой является основным строительным элементом данной фигуры. Она представляет собой математический объект без размеров и формы, который является базовым элементом в геометрии. Точка не имеет ни длины, ни ширины, ни высоты и обозначается обычно заглавной латинской буквой.
Прямая, на которой находится точка, является бесконечной протяженной геометрической фигурой, состоящей из бесконечного числа точек, расположенных в одной линии. Прямая не имеет ширины и толщины, но имеет длину. Она может быть горизонтальной, вертикальной или наклонной.
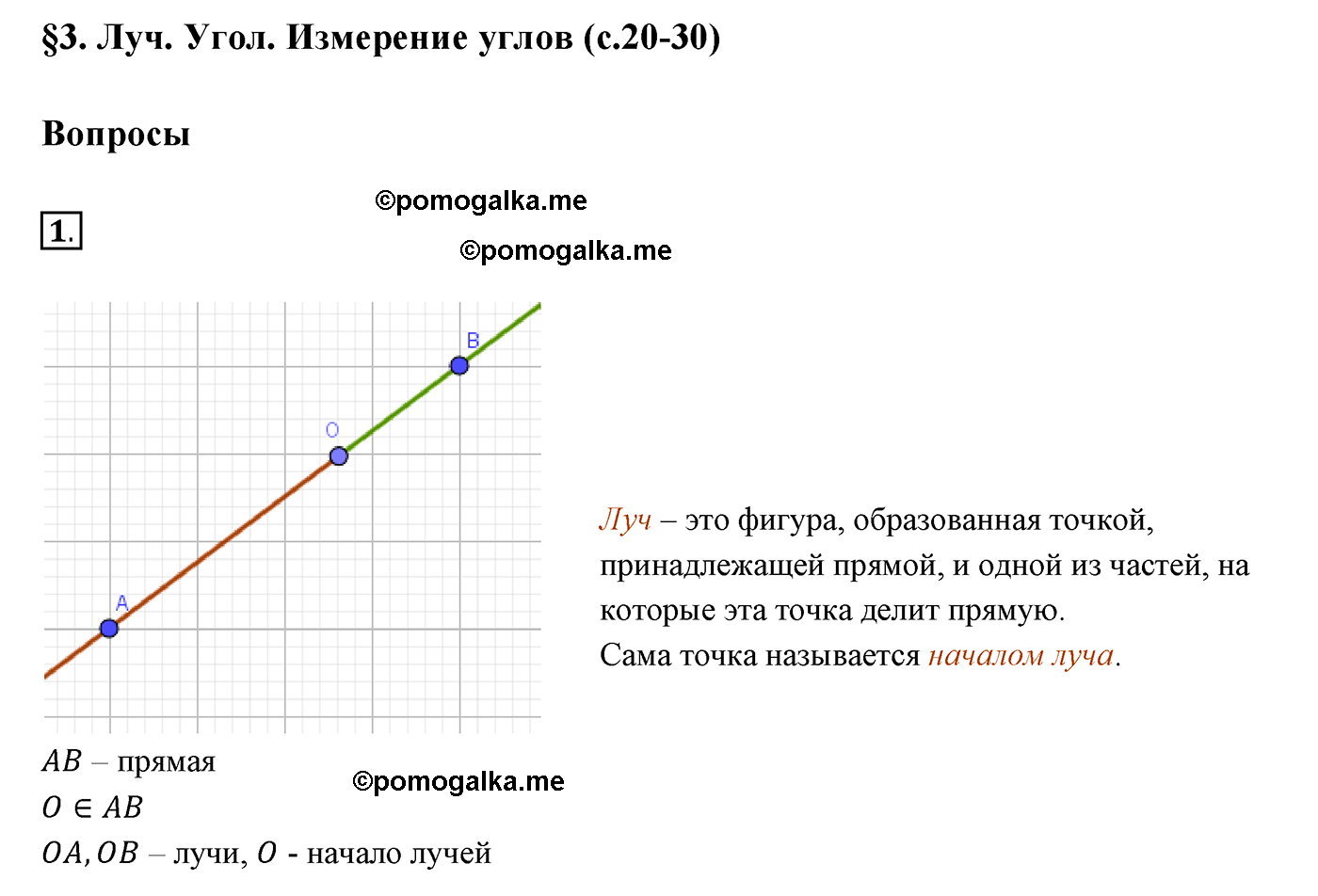
Когда точка находится на прямой, фигура образуется существованием двух полупрямых, состоящих из всех точек прямой, лежащих по разные стороны от данной точки. Эти полупрямые называются лучами. Одним из лучей является луч, проходящий через данную точку и расположенный на прямой слева от нее. Другим лучом является луч, проходящий через данную точку и расположенный на прямой справа от нее. Таким образом, фигура выглядит как два луча, выходящих из точки в разные стороны.
В геометрии такая фигура может называться «угол», обозначаясь обычно символом ∠. Угол состоит из трех элементов — вершины (точки) и двух сторон (лучей). Вершина угла является самой точкой, а стороны представляют собой лучи, исходящие из вершины и простирающиеся вдоль прямой. Угол обозначается небольшой дугой, которая соединяет стороны и указывает на место вершины.
Иными словами, фигура, образованная точкой на прямой, представляет собой угол, который определен своей вершиной и двумя сторонами-лучами. Такая геометрическая структура важна для изучения свойств углов и их применения в различных областях математики и физики.
Часть фигуры на которые

Фигура, образованная точкой, принадлежащей прямой, может быть разделена на несколько частей. В математике и геометрии такие части называются сегментами.
Сегмент — это часть фигуры, ограниченная прямыми или кривыми линиями, которые соединяют две точки на фигуре. В зависимости от формы фигуры, сегмент может быть прямолинейным, дугой, площадью и т.д.
Примеры сегментов фигуры:
- Прямолинейный сегмент: это часть фигуры, ограниченная двумя прямыми линиями, соединяющими две точки на фигуре.
- Дуговой сегмент: это часть фигуры, ограниченная дугой, которая соединяет две точки на фигуре.
- Площадной сегмент: это часть фигуры, ограниченная кривой линией или несколькими прямыми линиями, которые образуют замкнутую фигуру.
Сегменты фигур на плоскости играют важную роль в анализе и решении различных задач. Они могут быть использованы для определения площади фигуры, построения графиков функций, моделирования естественных и технических явлений, и многого другого.
Понимание сегментов фигуры на которые позволяет нам лучше понять и работать с геометрическими объектами, а также применять геометрию в реальных задачах и науке.
Название фигуры
Фигура, образованная точкой, принадлежащей прямой, и одной из частей, на которые она делит прямую, называется отрезок.
Отрезок — это часть прямой, ограниченная двумя точками, которые называются концами отрезка. Концы отрезка обозначаются буквами, например A и B, и записываются как AB или BA.
Свойства отрезка:
- Длина отрезка — это численная мера его длины. Длина отрезка AB обозначается как |AB| или AB.
- Отрезок может быть равным другому отрезку только если их длины равны. Например, если AB и CD имеют одинаковую длину, то AB = CD.
- Отрезок может быть больше или меньше другого отрезка в зависимости от их длин. Например, если AB > CD, то AB длиннее CD.
Измерение отрезка
Отрезок измеряется в единицах длины, таких как сантиметры (см), метры (м) или дюймы (дюйм). Для измерения отрезка используется линейка или мерная лента.
Примеры отрезков
Примеры отрезков: AB, CD, EF, GH. Длины отрезков могут быть разными: |AB| = 5 см, |CD| = 10 см, |EF| = 7 м, |GH| = 3 дюйма.
| Отрезок | Длина |
|---|---|
| AB | 5 см |
| CD | 10 см |
| EF | 7 м |
| GH | 3 дюйма |
Отрезки могут быть использованы в геометрии для построения других фигур, таких как треугольники, прямоугольники и многоугольники. Они имеют важное значение при изучении различных геометрических свойств и теорем.
Примеры фигур
Фигура, образованная точкой и прямой, называется отрезком. Отрезок имеет начальную и конечную точки, а также определенную длину. Он может быть вертикальным или горизонтальным.
Если отрезок с одним из своих концов продолжается в бесконечность, он называется полупрямой. Полупрямая имеет начальную точку и направление. Она может быть направлена вверх, вниз, влево или вправо.
Фигура, образованная двумя полупрямыми с общим началом, называется углом. Угол обозначается с помощью трех точек: вершины и двух точек на полупрямых, называемых сторонами. Угол может быть острым, прямым, тупым или развернутым.
Фигура, образованная двумя сторонами, имеющими общий конец, называется угловым участком. Угловой участок может быть ограничен кривыми линиями или заключен между двумя прямыми линиями.
Существуют и другие фигуры, образованные точками и прямыми, такие как многоугольники, окружности и эллипсы. Каждая из этих фигур имеет свои уникальные свойства и характеристики.
Вопрос-ответ:
Что такое фигура образованная точкой принадлежащей прямой и одной из частей, на которые она делит прямую?
Такая фигура называется отрезок.
Как называется фигура, образованная при пересечении прямой и плоскости и ограничивающая одну из их частей?
Такая фигура называется полуплоскость.
Как называется фигура, образованная пересечением двух перпендикулярных прямых?
Такая фигура называется угол.
Как называется фигура, образованная пересечением трех или большего числа прямых в одной точке?
Такая фигура называется вершина.
Как называется фигура, образованная пересечением плоскости и цилиндрической поверхности?
Такая фигура называется кривая.
Какая фигура образуется, когда точка лежит на прямой?
Если точка принадлежит прямой, то образуется линия.
