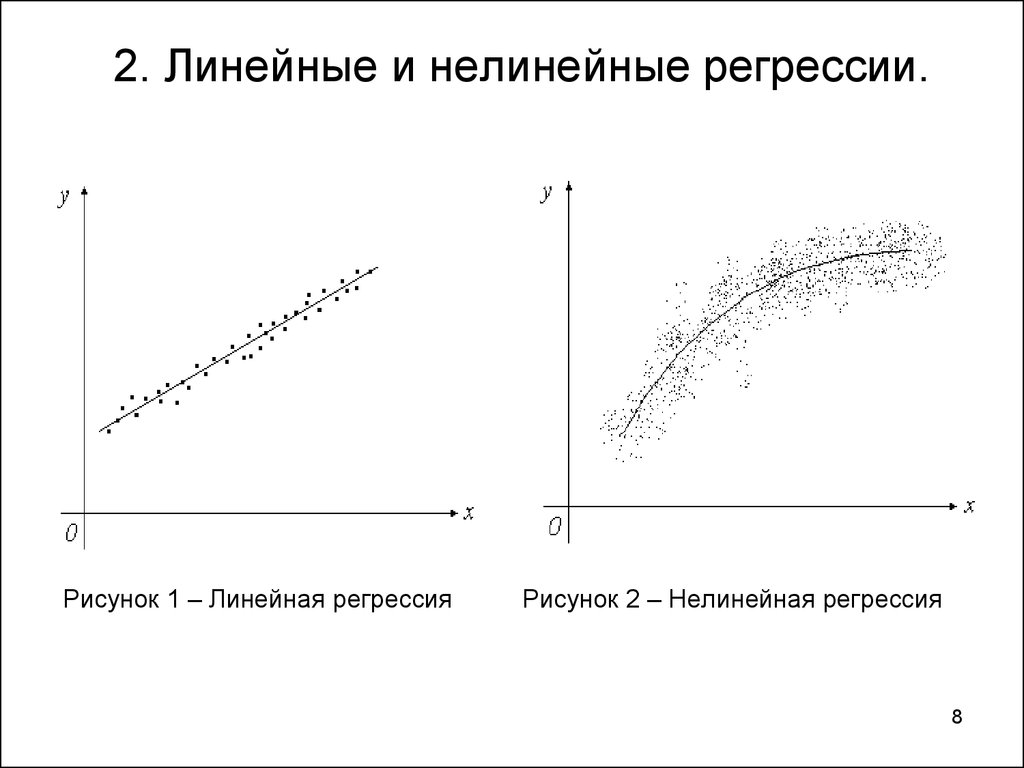
Регрессионная модель — это статистическая модель, используемая для предсказания значения одной переменной на основе значений других переменных. График регрессионной модели представляет собой визуализацию этой модели.
На графике регрессионной модели обычно изображена зависимость между независимой переменной (предиктором) и зависимой переменной (целевой переменной). Ось X обозначает значения предиктора, а ось Y — значения целевой переменной.
На графике регрессионной модели можно визуально определить, какие значения предиктора соответствуют каким значениям целевой переменной, и насколько сильна эта связь. Он позволяет представить результаты анализа регрессии в понятной и наглядной форме.
Что такое регрессионная модель?
Регрессионная модель может быть использована для решения различных задач, таких как прогнозирование, классификация и понимание факторов, влияющих на исследуемый процесс или явление.
Основные компоненты регрессионной модели
Основными компонентами регрессионной модели являются:
- Независимые переменные (предикторы) — переменные, которые используются для предсказания зависимой переменной.
- Зависимая переменная (результат) — переменная, которая предсказывается с помощью независимых переменных.
- Параметры модели — константы, которые определяют форму и свойства регрессионной модели.
Виды регрессионных моделей
Существует несколько видов регрессионных моделей, которые могут быть использованы в зависимости от природы данных и исследуемого явления. Одним из наиболее распространенных является линейная регрессия, где связь между независимыми и зависимой переменными считается линейной.
Другие виды регрессионных моделей включают логистическую регрессию, полиномиальную регрессию и лассо-регрессию. Каждый из них имеет свои особенности и применяется в различных ситуациях.
Регрессионные модели являются важным инструментом статистического анализа и позволяют исследователям и аналитикам делать предсказания и устанавливать связи между переменными, что помогает в понимании и объяснении реальных явлений и процессов.
Определение регрессионной модели
В регрессионной модели используется график, называемый «график регрессии», который визуально отображает эту связь. На графике регрессии независимая переменная обычно откладывается по оси X, а зависимая переменная — по оси Y. Точки на графике представляют значения зависимой и независимой переменных, а линия регрессии показывает приближенное соотношение между ними.
График регрессии имеет большое значение при анализе данных и построении регрессионных моделей, потому что он позволяет визуально оценить, насколько хорошо модель соответствует данным. Если точки на графике расположены близко к линии регрессии, то модель хорошо объясняет данные. Если точки разбросаны далеко от линии регрессии, то модель плохо объясняет данные и может быть неадекватной.
График регрессии может быть построен в программных средствах для статистического анализа, таких как Python, R или Excel. По графику также можно определить, есть ли в данных явная линейная зависимость или возможны иные виды зависимостей, например, параболическая или экспоненциальная.
Цель регрессионной модели

Регрессионные модели широко используются в статистике и машинном обучении для решения различных задач, таких как прогнозирование временных рядов, анализ социально-экономических данных, определение причинно-следственных связей и многое другое.
Целью регрессионной модели может быть как построение точных прогнозов, так и понимание факторов, которые влияют на изменение зависимой переменной. Построение хорошей регрессионной модели требует правильного выбора независимых переменных, а также оценки и интерпретации коэффициентов модели.
Применение регрессионной модели
Применение регрессионной модели широко распространено во многих областях, включая экономику, финансы, бизнес, медицину и многие другие. С помощью регрессионной модели можно предсказывать будущие значения зависимой переменной на основе имеющихся данных.
Прогнозирование с использованием регрессионной модели основывается на анализе и моделировании связи между зависимой переменной и набором независимых переменных. Результаты регрессионной модели могут быть представлены в виде графика, который иллюстрирует эту связь.
График регрессионной модели позволяет визуализировать как зависимую переменную, так и независимые переменные, а также их взаимосвязь. Он графически отображает тренд связи между переменными и позволяет провести анализ и оценку этой связи.
Помимо прогнозирования будущих значений, регрессионная модель также может использоваться для анализа и изучения влияния независимых переменных на зависимую переменную. Она помогает выявить значимые факторы, которые влияют на изменение зависимой переменной и определить их вклад в ее значения.
Таким образом, применение регрессионной модели важно для получения более глубокого понимания и анализа взаимосвязей между переменными и позволяет принимать более обоснованные решения на основе этих связей.
Какая информация содержится в регрессионной модели?
1. Коэффициенты регрессии
Одна из основных частей регрессионной модели — это коэффициенты регрессии. Они показывают, какие изменения в значениях независимых переменных приводят к изменениям в зависимой переменной. Каждая независимая переменная имеет свой собственный коэффициент, который показывает величину и направление влияния этой переменной на зависимую переменную.
2. P-значения
P-значения позволяют оценить статистическую значимость коэффициентов регрессии. Они показывают вероятность того, что наблюдаемое значение коэффициента могло возникнуть случайно при нулевой гипотезе (т.е. при отсутствии связи между переменными). Малое p-значение указывает на то, что связь статистически значима.
3. Стандартные ошибки
Стандартные ошибки показывают, насколько точно прогнозируются коэффициенты регрессии. Они являются мерой неопределенности оценок коэффициентов и позволяют оценить их значимость. Малые стандартные ошибки указывают на более точные оценки коэффициентов.
4. Остатки
Остатки регрессионной модели показывают разницу между фактическими значениями зависимой переменной и значениями, предсказанными регрессионной моделью. Анализ остатков может помочь выявить наличие систематических ошибок модели и проверить ее адекватность.
Интерпретация результатов регрессионной модели

Интерпретация результатов регрессионной модели основана на основных характеристиках модели, таких как коэффициенты регрессии, стандартные ошибки коэффициентов и значения t-статистики и p-значения.
Коэффициенты регрессии
Коэффициенты регрессии показывают, как изменение в независимой переменной влияет на изменение зависимой переменной. Знак коэффициента показывает направление этого влияния, а его величина — силу влияния. Например, если коэффициент регрессии положителен, то увеличение значения независимой переменной будет приводить к увеличению значения зависимой переменной.
Стандартные ошибки коэффициентов
Стандартные ошибки коэффициентов показывают, насколько точно оценены коэффициенты регрессии. Чем меньше стандартная ошибка, тем более точная оценка коэффициента. Стандартные ошибки также используются для вычисления доверительных интервалов и проведения статистических тестов на значимость коэффициентов.
Значения t-статистики и p-значения используются для проверки гипотезы о значимости коэффициентов регрессии. Если p-значение ниже выбранного уровня значимости (как правило, 0,05), то мы можем считать коэффициент статистически значимым. Это означает, что изменения в независимой переменной имеют реальное влияние на зависимую переменную.
Каким образом регрессионная модель может помочь в анализе данных?
1. Предсказание значений
Регрессионная модель позволяет предсказывать значения одной переменной на основе другой или нескольких других переменных. Например, с помощью такой модели можно предсказать цену недвижимости на основе различных факторов, таких как площадь, количество комнат, год постройки и т.д. Такие прогнозы могут быть полезными для принятия решений в различных отраслях, от финансов до маркетинга.
2. Анализ влияния переменных
Регрессионная модель позволяет анализировать влияние различных факторов на зависимую переменную. С помощью такой модели можно определить, какие переменные оказывают наибольшее влияние на результат и насколько сильно это влияние является статистически значимым. Такой анализ может помочь в выявлении ключевых факторов, которые необходимо учесть при принятии решений.
Регрессионная модель – мощный инструмент в анализе данных, который позволяет строить прогнозы и анализировать зависимость между переменными. Она может быть полезна для принятия решений в различных сферах, от бизнеса до науки. Однако, при использовании такой модели необходимо учитывать ее ограничения и особенности, чтобы получить достоверные и полезные результаты.
Какие методы используются для создания регрессионной модели?
Существует несколько методов, которые могут быть использованы для создания регрессионных моделей. Некоторые из них включают:
- Метод наименьших квадратов (ordinary least squares, OLS): он является одним из самых распространенных и простых методов. Он заключается в поиске линии наилучшего соответствия между зависимой переменной и независимыми переменными.
- Метод регуляризации: это метод, который помогает бороться с проблемой переобучения модели путем добавления штрафных членов к функции потерь. Наиболее известными методами регуляризации являются гребневая регрессия (ridge regression) и лассо-регрессия (lasso regression).
- Метод опорных векторов (support vector regression, SVR): он использует концепцию опорных векторов для создания регрессионной модели. Он пытается найти гиперплоскость, наилучшим образом разделяющую данные.
- Метод случайного леса (random forest regression): это алгоритм, основанный на построении ансамбля деревьев решений. Каждое дерево прогнозирует результат, и затем средние значения прогнозов используются для определения окончательного результата.
Каждый из этих методов имеет свои преимущества и недостатки, и выбор метода зависит от конкретной задачи и доступных данных.
Как называется график, отображающий регрессионную модель?
График, отображающий регрессионную модель, называется линейная регрессионная модель. Он представляет собой графическое изображение зависимости между независимой переменной и зависимой переменной в модели.
За основу графика линейной регрессионной модели берутся отдельные пары значений независимой и зависимой переменных. Эти значения обычно привязываются к точкам на графике. Затем строится линия регрессии, которая наилучшим образом описывает связь между переменными. Линия регрессии проходит через центр масс точек на графике и показывает основную тенденцию в данных.
График линейной регрессионной модели позволяет визуализировать и анализировать взаимосвязь между переменными. Он также может использоваться для прогнозирования значений зависимой переменной на основе независимой переменной.
Вопрос-ответ:
Как называется график регрессионной модели?
График регрессионной модели называется линейная регрессионная прямая.
Как построить график регрессионной модели?
Для построения графика регрессионной модели необходимо взять данные, на которых требуется провести анализ, и подобрать уравнение линейной регрессии. Затем строится график, где по оси X откладываются независимые переменные, а по оси Y — зависимые переменные. На графике отображается линия, которая наилучшим образом приближает данные и показывает взаимосвязь между переменными.
Какая информация можно получить из графика регрессионной модели?
Из графика регрессионной модели можно получить информацию о взаимосвязи между независимыми и зависимыми переменными. Он позволяет визуализировать и понять, как одна переменная влияет на другую. Также график может помочь в предсказании значений зависимой переменной при заданных значениях независимых переменных.
Какая форма имеет график регрессионной модели?
Форма графика регрессионной модели зависит от типа модели. В случае линейной регрессии форма графика будет прямой линией, которая наилучшим образом приближает данные. В других типах моделей форма графика может быть кривой или иным образом отличаться от прямой.
Как интерпретировать график регрессионной модели?
График регрессионной модели можно интерпретировать следующим образом: если линия регрессии возрастает, то зависимая переменная увеличивается с увеличением независимой переменной. Если линия регрессии убывает, то зависимая переменная уменьшается с увеличением независимой переменной. Если линия горизонтальная, то зависимая переменная не зависит от изменения независимой переменной.
Как называется график регрессионной модели?
График регрессионной модели называется линейная регрессия. Он представляет собой прямую линию, которая показывает зависимость между независимой и зависимой переменными. На графике можно увидеть, как изменение одной переменной влияет на изменение другой.