Y(x) является функцией ключевыми моментами и служит для описания зависимости переменной Y от переменной x. Данная функция широко используется в различных областях науки и техники, а также в математическом анализе, физике и экономике для моделирования и предсказания различных процессов и явлений.
Основное применение функции Y(x) заключается в том, чтобы установить зависимость переменной Y от переменной x. Это позволяет исследовать, какое влияние имеют изменения x на Y и наоборот. Таким образом, функция Y(x) позволяет установить закономерности и выявить взаимосвязи между двумя переменными.
Определение функции Y(x) может варьироваться в зависимости от конкретной задачи или области применения. Однако в основе функции всегда лежит идея определить значение переменной Y в зависимости от значения переменной x. Функция Y(x) может быть задана аналитически, в виде математического выражения, или же может быть задана графически, в виде графика или диаграммы.
Функция Y x: основные моменты и свойства
Функция Y x может иметь различные формы и графики в зависимости от своего определения. Каждая конкретная функция Y x обладает своими особыми свойствами и характеристиками, которые определяют ее поведение и функциональность.
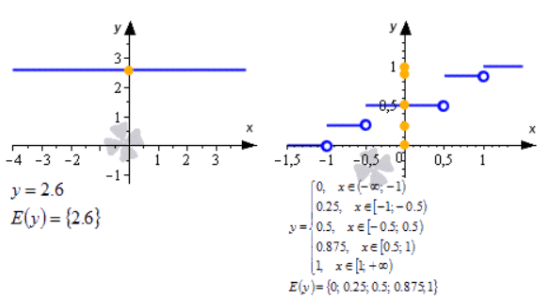
Одним из важных свойств функции Y x является ее область определения, то есть множество всех допустимых значений аргумента x. В зависимости от типа функции, область определения может быть ограниченной или неограниченной.
Еще одним важным свойством функции Y x является ее область значений, то есть множество всех возможных значений функции Y при заданных значениях аргумента x. Область значений может быть ограниченной или неограниченной в зависимости от типа функции.
Кроме того, функция Y x может быть задана явным или неявным способом. Явная функция задается в виде явной формулы, где значение Y выражается явно через значение x. Неявная функция же задается в виде уравнения, где значение Y определено неявно через значение x.
Функция Y x является основой для многих других математических понятий и теорий. Она широко применяется во многих областях науки, техники, экономики и других сферах деятельности. Понимание основных моментов и свойств функции Y x является необходимым условием для понимания и использования более сложных математических концепций.
Определение и назначение функции Y x
Функция Y x имеет различные применения в различных областях науки и техники. Она может использоваться для описания зависимости одной переменной от другой, для моделирования различных физических, экономических или социальных явлений. Функция Y x может также использоваться для аппроксимации данных или построения графиков.
Определение функции Y x может быть различным в зависимости от контекста. Например, в математике функция Y x может быть определена аналитически или задана в виде таблицы значений. В программировании функция Y x может быть описана в виде кода или функции.
Независимо от способа определения, функция Y x играет важную роль в решении задач и исследовании различных явлений, позволяя анализировать зависимости и делать прогнозы.
Что такое функция Y x
Функция Y x может быть представлена в виде уравнения, графика или таблицы значений. Она позволяет нам лучше понять взаимосвязь между переменными и описать различные закономерности.
Функция Y x может иметь различные свойства, такие как монотонность, четность, периодичность и др. Она может быть задана аналитически или геометрически.
Определение функции Y x включает в себя область определения (множество значений x), область значений (множество значений y) и правило соответствия между ними.
Функция Y x может быть линейной, квадратичной, степенной, тригонометрической, логарифмической и т. д. Каждый тип функции имеет свои особенности и применения в различных областях науки и техники.
Изучение функций Y x является важной частью математического образования и позволяет нам анализировать и решать различные задачи: находить корни уравнений, определять экстремумы функций, строить графики и многое другое.
Как работает функция Y x
Определение функции Y x заключается в указании математического связи между переменными Y и x. Значение переменной Y зависит от значения переменной x в соответствии с определенными правилами или закономерностями.
Основные моменты работы функции Y x:
| Момент | Описание |
|---|---|
| Аргумент | x является аргументом функции Y x. Он может принимать различные значения, которые влияют на значение Y. |
| Значение | Функция Y x возвращает значение переменной Y в зависимости от значения аргумента x. Это значение может быть числом, буквой или символом. |
| График | Функцию Y x можно представить в виде графика, который отображает зависимость между значениями Y и x. График может иметь различную форму, в зависимости от математической связи. |
| Таблица | Функция Y x может быть представлена в виде таблицы, в которой указываются значения переменных Y и x для различных аргументов. Таблица позволяет легче анализировать значения функции. |
Таким образом, функция Y x является важным математическим понятием, которое позволяет описывать и анализировать зависимости между переменными Y и x. Она имеет различные формы представления, включая уравнение, график и таблицу.
Области применения и значимость функции Y x
Функция Y(x) имеет широкий спектр применения в различных областях, таких как:
| Область применения: | Значимость: |
| Математика | Функция Y(x) используется для решения уравнений, построения графиков и анализа математических моделей. |
| Физика | Функция Y(x) применяется для описания движения тела, распределения энергии и других физических процессов. |
| Экономика | Функция Y(x) применяется для моделирования роста и снижения цен, определения спроса и предложения на рынке. |
| Инженерия | Функция Y(x) используется для решения инженерных задач, таких как определение напряжения, силы и деформации. |
| Компьютерная наука | Функция Y(x) применяется для разработки алгоритмов, обработки данных, искусственного интеллекта и машинного обучения. |
Области применения функции Y(x) являются универсальными, а ее значимость заключается в возможности описания, моделирования и прогнозирования множества физических, экономических и математических процессов.
Ключевые свойства функции Y x
Функция Y x имеет следующие ключевые свойства:
1. Определение функции: Функция Y x представляет собой математическое правило, которое связывает каждому значению x соответствующее значение Y.
2. Область определения: Функция Y x определена для определенного множества значений x. Это может быть множество действительных чисел, целых чисел или других числовых доменов.
3. Область значений: Функция Y x может принимать только определенные значения Y в зависимости от значений x. Область значений может быть любым множеством чисел или точек.
4. График функции: Функцию Y x можно представить графически на координатной плоскости. График функции показывает соответствие между значениями x и соответствующими значениями Y.
5. Зависимость: Значение Y зависит от значения x в функции Y x. Изменение значения x приводит к изменению значения Y.
6. Монотонность: Функция Y x может быть монотонно возрастающей или убывающей, в зависимости от изменения значений x.
7. Периодическость: Некоторые функции Y x могут быть периодическими, то есть иметь определенный период повторения значений.
Это основные ключевые свойства функции Y x, которые помогают анализировать и понимать ее строение и свойства.
Однозначность и многозначность функции Y x
Однозначность функции означает, что каждому значению переменной x на промежутке соответствует ровно одно значение функции Y. То есть, при заданных значениях x функция должна давать только один результат. Если функция удовлетворяет этому свойству, она называется однозначной.
Многозначность функции означает, что одному значению переменной x на промежутке может соответствовать несколько значений функции Y. То есть, функция может давать разные результаты при одном и том же значении x. Если функция не удовлетворяет свойству однозначности, она называется многозначной.
Определение однозначности или многозначности функции зависит от ее формулы и поведения на всем промежутке значений переменной x. Например, функция может быть однозначной на всей числовой прямой, а может быть однозначной только на определенном промежутке значений x.
Непрерывность и дифференцируемость функции Y x
Для того чтобы функция была непрерывной на интервале, необходимо, чтобы:
- Функция была определена на этом интервале.
- Лимит функции в каждой точке этого интервала существовал и равнялся значению функции в этой точке.
Дифференцируемость функции Y x — это свойство функции иметь производную в каждой точке своей области определения. Функция называется дифференцируемой на некотором интервале, если она дифференцируема в каждой точке этого интервала.
Производная функции в точке определяется как предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю.
Важно понимать, что непрерывность функции не является достаточным условием ее дифференцируемости. Некоторые функции могут быть непрерывными, но не дифференцируемыми.
Для дифференцируемости функции также необходимо, чтобы она была непрерывной. Дифференцируемая функция также является непрерывной, но не наоборот.
Монотонность и выпуклость функции Y x
Монотонность функции Y x описывает ее поведение в зависимости от изменения аргумента x. Если функция Y x увеличивается при увеличении x или убывает при уменьшении x, то она называется монотонно возрастающей или монотонно убывающей соответственно.
Выпуклость функции Y x связана с ее кривизной. Если для любых двух точек x1 и x2 на графике функции Y x отрезок, соединяющий эти точки, лежит выше графика, то функция называется выпуклой вниз (выпуклой вверх) в области между этими точками. Если для любых двух точек x1 и x2 на графике функции Y x отрезок, соединяющий эти точки, лежит ниже графика, то функция называется вогнутой вниз (вогнутой вверх) в области между этими точками.
Определение монотонности и выпуклости функции Y x может быть полезным для анализа ее свойств и поведения, а также для принятия решений в различных областях науки, техники и экономики. С помощью этих понятий можно оценивать изменение функции при вариации аргумента и прогнозировать ее поведение в различных ситуациях.
Вопрос-ответ:
Зачем нужна функция ключевые моменты в программировании?
Функция ключевые моменты в программировании нужна для идентификации и определения наиболее значимых и важных моментов в программе. Она позволяет выделить основные шаги и операции, которые должны быть выполнены для достижения определенной цели.
Что включает в себя функция ключевые моменты?
Функция ключевые моменты включает в себя определение и описание наиболее важных этапов выполнения программы. Это могут быть блоки кода, условные операторы, функции и другие элементы, которые необходимы для достижения конкретной цели программы.
Как определить функцию ключевые моменты в программе?
Для определения функции ключевые моменты в программе нужно анализировать заявленные требования и задачи, которые должна выполнять программа. Затем нужно идентифицировать основные шаги и моменты, которые необходимы для достижения этих целей. Это можно сделать путем разделения функционала программы на более мелкие блоки и описания каждого блока как ключевого момента.
Какие преимущества имеет использование функции ключевые моменты в программировании?
Использование функции ключевые моменты в программировании позволяет сделать код более понятным и структурированным. Она упрощает понимание программы другим разработчикам и позволяет быстрее входить в проект. Кроме того, функция ключевые моменты позволяет выделить и сосредоточить внимание на самых важных и критических моментах в программе, что может быть полезно при отладке и оптимизации кода.
Какие методы можно использовать для определения функции ключевые моменты?
Для определения функции ключевые моменты в программе можно использовать различные методы, включая декомпозицию программы на более мелкие компоненты, анализ требований и задач, использование структур данных (например, деревья), а также учет опыта и интуиции разработчика.
Что такое функция?
Функция — это математический объект, который связывает каждый элемент из одного множества (называемого областью определения) с элементом из другого множества (называемого областью значений) таким образом, что каждому элементу области определения соответствует только один элемент области значений.