Названия компонентов при сложении в математике

Математика – точная наука, в которой важно правильно называть все составляющие процессы и элементы. Одним из самых простых и исключительно важных арифметических действий является сложение. Но мало кто задумывается о том, как правильно называются его компоненты. Оказывается, при сложении в математике есть специальные термины, которыми обозначаются эти самые компоненты. Давайте разберемся, как они называются.

Первый компонент сложения называется слагаемое. Это числовое значение, которое прибавляется к другому числу или к результирующей сумме. Слагаемые могут быть положительными или отрицательными, они определяются знаком числа. Например, в выражении «2 + 3 = 5» числа 2 и 3 являются слагаемыми.

Второй компонент сложения называется слагаемое. Оно также является числовым значением, которое складывается с другими числами или с результирующей суммой. Слагаемые могут иметь положительный или отрицательный знак, а их значение может быть как целым числом, так и десятичной дробью. Например, в выражении «5 + (-3) = 2» первое слагаемое – 5, а второе слагаемое – (-3).

Сложение в математике: основные понятия

В сложении присутствуют следующие понятия:

• Слагаемые: это числа, которые складываются. Они являются компонентами сложения и обозначаются буквами или цифрами. Например, в сложении 3 + 5 = 8, числа 3 и 5 являются слагаемыми.
• Сумма: результат сложения слагаемых. Обозначается символом «+». В примере 3 + 5 = 8, число 8 является суммой слагаемых 3 и 5.
• Знак сложения: символ «+», который обозначает операцию сложения.

При сложении чисел важно запомнить, что порядок слагаемых не влияет на сумму. Например, 3 + 5 и 5 + 3 дают одинаковый результат — 8. Это свойство называется коммутативностью сложения.

Сложение в математике имеет широкое применение в повседневной жизни. Оно используется для подсчета денег, времени, расчета расстояний и многих других задач.

Сложение: определение и принцип

Компоненты при сложении называются слагаемыми. Процесс сложения можно представить себе, как объединение двух или более групп предметов в одну общую группу.

При сложении чисел принцип его выполнения заключается в следующем: слагаемые суммируются по каждому разряду, начиная справа и переносом единицы на следующий разряд, если сумма превышает десять.

Например, при сложении чисел 24 и 17:

24

+ 17

——

Сначала складываем единицы (4 + 7 = 11), получаем 1 в единицах и переносим 1 в десятки. Затем складываем десятки (2 + 1 = 3), и получаем итоговую сумму 31.

Таким образом, сложение позволяет находить общую сумму данных чисел и является основой для более сложных операций в математике.

Сложение — операция математического сложения

Компоненты сложения могут быть любыми числами – как положительными, так и отрицательными. Однако при сложении обычно используются целые положительные числа.

Операция сложения обозначается знаком «+». Например, сложение числа 3 и числа 4 обозначается как 3 + 4, и результатом этой операции будет число 7.

Чтобы выполнить сложение, необходимо провести следующие шаги:

1. Выбрать два или более числа, которые нужно сложить. Эти числа называются компонентами сложения.
2. Расположить компоненты сложения так, чтобы их цифры одного разряда были вертикально выровнены.
3. Начиная с крайнего правого разряда, сложить цифры каждого разряда в столбик и записать полученную сумму.
4. Если в одном разряде сумма двух чисел больше 9, то учитывается только единицы разряда. Десятки переносятся в следующий разряд.
5. В случае необходимости, дополнить разряды чисел нулями перед сложением.
6. Полученная сумма является результатом сложения.

Например, при сложении чисел 345 и 123:

345
+  123
______
468

Результатом сложения чисел 345 и 123 будет число 468.

Сложение позволяет совершать множество различных операций, как в повседневной жизни, так и в различных областях науки. Оно является основой для более сложных операций, таких как умножение, деление и вычитание.

Принцип сложения: свойства и правила

Слагаемые — это числа или выражения, которые складываются в процессе операции. Одно слагаемое может быть положительным, отрицательным, или нулем.

Сумма — это результат сложения слагаемых. Она обозначается знаком «+».

Для проведения операции сложения существуют следующие правила и свойства:

• Коммутативность: порядок слагаемых не влияет на результат сложения. Например, a + b = b + a.
• Ассоциативность: результат сложения трех или более чисел не зависит от порядка их группировки. Например, (a + b) + c = a + (b + c).
• Существование нейтрального элемента: сложение числа с нулем не меняет значение числа. Например, a + 0 = a.
• Существование противоположного элемента: для любого числа a существует такое число -a, что a + (-a) = 0.
• Ассоциативность относительно умножения: результат сложения и умножения двух чисел не зависит от порядка их операций. Например, a * (b + c) = (a * b) + (a * c).

Эти свойства и правила сложения позволяют упростить вычисления и облегчают работу с числами в математике.

Слагаемые: компоненты сложения

Слагаемые могут быть различной природы: числами, переменными, выражениями и даже функциями. Главное условие — они должны быть однородными и соответствовать одной операции сложения.

Примеры слагаемых:

1. Сумма чисел: 2 + 3 = 5. Здесь 2 и 3 — это слагаемые.
2. Сумма переменных: x + y.
3. Сумма выражений: (2x + y) + (3y — x).
4. Сумма функций: f(x) + g(x).

Знание о слагаемых и их свойствах позволяет более глубоко и точно разбираться в процессе арифметических операций сложения и выполнять сложение с высокой точностью.

Слагаемое: определение и роль

Компоненты, которые участвуют в сложении, называются слагаемыми. Слагаемое — это число или выражение, которое при сложении с другим числом приводит к получению суммы. Например, в выражении 5 + 3 = 8, числа 5 и 3 являются слагаемыми, а 8 — суммой.

Роль слагаемых в сложении заключается в определении их вклада в общую сумму. Каждое слагаемое представляет определенное количество или величину, которая при сложении со всеми остальными слагаемыми приводит к получению окончательной суммы.

В сложении можно использовать различные типы чисел, такие как целые числа, вещественные числа, рациональные числа и другие. Количество слагаемых может быть разным, от двух и более. Важно помнить, что порядок слагаемых в сложении не влияет на результат, то есть сумма будет одинакова, независимо от того, в каком порядке записаны слагаемые.

Знание и понимание концепции слагаемых является важным базовым навыком в математике и нужно для решения различных задач, а также для более сложных операций, таких как умножение и деление.

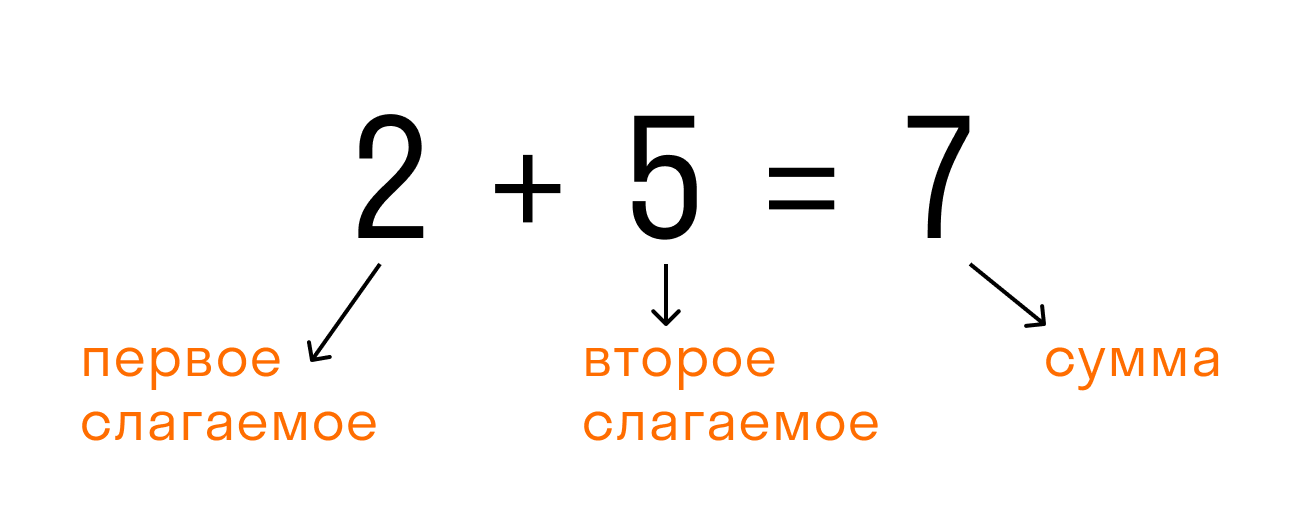
Первое слагаемое и второе слагаемое

Первое слагаемое – это число, которое мы начинаем считать применительно к сложению. Оно обычно записывается первым слагаемым и находится слева от знака «+» или между скобками.

Второе слагаемое – это число, которое мы прибавляем к первому слагаемому при сложении. Оно обычно записывается вторым слагаемым и находится справа от знака «+» или между скобками.

Например, при сложении чисел 5 и 3, число 5 является первым слагаемым, а число 3 – вторым слагаемым. Выражение для данного сложения будет выглядеть так: 5 + 3.

Обратите внимание, что порядок записи слагаемых может влиять на результат сложения. Это объясняется свойствами операции сложения. Например, при сложении чисел 3 и 5 мы получим разный результат, если поменяем местами слагаемые: 3 + 5 ≠ 5 + 3.

Знание и понимание понятий первого и второго слагаемого важны для успешного выполнения математических операций сложения и понимания свойств этой операции.

Сумма: результат сложения

В математике слагаемые или сумманды могут быть числами, переменными, выражениями или даже функциями. Результат сложения может быть также числом, переменной или выражением, в зависимости от типа слагаемых.

Например, если мы хотим найти сумму чисел 3 и 5, мы складываем их и получаем результат — число 8. В этом случае 3 и 5 являются слагаемыми, а 8 — суммой.

Сумма может быть найдена с помощью специального математического знака «+», который означает операцию сложения. Например, для чисел a и b сумма будет записываться как a + b.

Кроме того, сумма может быть представлена в виде алгебраического выражения или уравнения, где слагаемые могут быть переменными или выражениями. Например, сумма выражения 2x + 3y и выражения 4x — 2y будет записываться как (2x + 3y) + (4x — 2y).

Таким образом, сумма представляет собой результат сложения компонентов и может иметь различные формы в зависимости от типа слагаемых.

Вопрос-ответ:

Какие компоненты можно сложить в математике?

В математике можно сложить различные компоненты, например, числа, мономы, полиномы, векторы и так далее.

Что такое компоненты в математике?

Компоненты в математике — это отдельные элементы или составляющие, которые можно сложить вместе для получения результата.

Как называются отдельные элементы при сложении в математике?

Отдельные элементы при сложении в математике могут называться различными терминами, например, слагаемыми, аддендами или компонентами. Название зависит от конкретного контекста и предметной области.

Какие основные понятия используются при сложении в математике?

Основные понятия, используемые при сложении в математике, включают слагаемые, сумму, индексы суммирования и операцию сложения.

Что такое сумма в математике?

Сумма в математике — это результат операции сложения, при которой два или более компонентов объединяются в один элемент.

Какие компоненты есть в математике?

В математике есть различные компоненты, включая числа, переменные, операторы и функции.