Как фигуры называются

Фигуры вокруг нас — это неотъемлемая часть нашей повседневной жизни. Они покрыты загадкой и таинством, привлекая внимание и вызывая интерес. Но как эти удивительные многогранные объекты именуются? Хотите узнать?

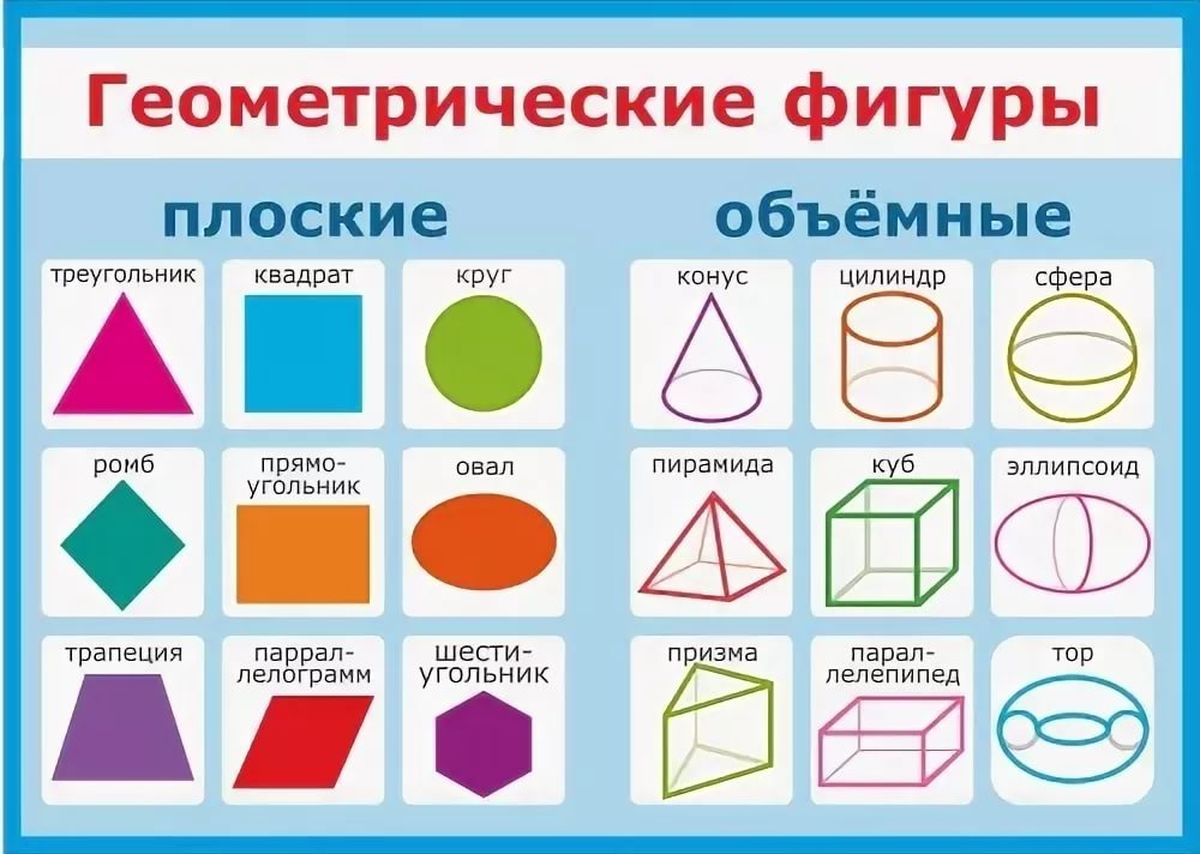
В мире геометрии фигуры делятся на две большие категории: плоские и пространственные. Плоские фигуры занимают только одну плоскость, как, например, треугольник, квадрат или окружность. Пространственные фигуры, в свою очередь, занимают несколько плоскостей и имеют объем, такие как параллелепипед, конус или шар.

Но остановимся на плоских фигурах. Среди них выделяются фигуры со сторонами: треугольник, квадрат, прямоугольник, ромб, параллелограмм. Каждая из них имеет свои уникальные особенности и свойства. Видя эти фигуры, мы мгновенно узнаем их форму и название благодаря знанию геометрии.

Обзаведясь знаниями о названии фигур, можно играть в увлекательные интеллектуальные игры, решать головоломки и задачи, а также применять их в повседневной жизни. Познакомьтесь с миром названий фигур и расширьте свои границы!

Содержание

Как называются фигуры?

Фигуры в геометрии могут иметь различные имена и свойства. Познакомимся с некоторыми из них:

Треугольник

Треугольник — это фигура, у которой три стороны и три угла. Треугольники могут быть различных типов, таких как равносторонний, равнобедренный или разносторонний.

Прямоугольник

Прямоугольник — это четырехугольник, у которого противоположные стороны равны и все углы прямые. Прямоугольники имеют две пары параллельных сторон.

Круг

Круг — это множество точек на плоскости, равноудаленных от одной фиксированной точки. Все точки на окружности имеют одинаковое расстояние до центра круга.

Квадрат

Квадрат — это ромб, у которого все стороны равны и все углы прямые. Каждая сторона квадрата параллельна и равна другой стороне.

Это только некоторые из самых известных и распространенных фигур в геометрии. Существует еще множество других интересных фигур с различными свойствами и именами.

Геометрические фигуры

Прямоугольник

Прямоугольник — это четырехугольник с четырьмя прямыми углами и противоположные стороны, которые параллельны и равны по длине. Он имеет две пары противоположных сторон, которые параллельны и равны друг другу.

Круг

Круг — это двумерная геометрическая фигура, которая состоит из всех точек, находящихся на одинаковом расстоянии от центра. Он имеет радиус, диаметр и окружность, которая является границей круга.

Треугольник

Треугольник — это трехугольник с тремя сторонами и тремя углами. У него есть разные виды, такие как равносторонний треугольник, равнобедренный треугольник и прямоугольный треугольник.

Квадрат

Квадрат — это четырехугольник с четырьмя равными сторонами и четырьмя прямыми углами. У него также есть две пары противоположных сторон, которые параллельны и равны по длине.

Все эти геометрические фигуры имеют свои особенности и применения в разных областях науки и жизни.

Прямоугольник и его свойства

Стороны: Прямоугольник имеет две пары сторон, противоположные стороны равны и параллельны друг другу.
Углы: Все углы прямоугольника равны 90 градусов, что делает его остроугольным.
Периметр: Периметр прямоугольника вычисляется путем сложения всех его сторон.
Площадь: Площадь прямоугольника вычисляется умножением длины одной из его сторон на длину противоположной стороны.
Диагонали: Прямоугольник имеет две диагонали, которые соединяют его противоположные углы.
Диагонали: Прямоугольник также обладает центральной симметрией, что означает, что его можно разделить на две равные половины, отражающие друг друга.
Примеры: Некоторые известные примеры прямоугольников включают окна, столы и книги.

Квадрат и его особенности

Все четыре стороны квадрата равны между собой, поэтому его можно назвать равносторонним.
Углы квадрата также равны между собой и составляют 90 градусов. Все углы квадрата прямые.
Диагонали квадрата делят его на четыре треугольника, которые тоже являются равнобедренными и равносторонними.
Периметр квадрата равен сумме длин всех его сторон.
Площадь квадрата вычисляется по формуле: S = a^2, где а – длина стороны квадрата.

Квадрат является одной из основных и наиболее изучаемых фигур в геометрии. Он широко применяется в различных областях, включая строительство, дизайн, математику и программирование.

Круг — фигура с безграничным количеством точек

Круг имеет много других характеристик, включая радиус и диаметр. Радиус круга — это расстояние от центральной точки круга до любой точки на его границе. Диаметр круга — это отрезок прямой, проходящий через центр круга и имеющий концы на его границе.

Свойства круга:

Круг является выпуклой фигурой, то есть все его точки лежат внутри фигуры;
Длина окружности круга равна 2πr, где r — радиус круга;
Площадь круга вычисляется по формуле πr^2, где π (pi) — приближенное значение равное 3.14159;
Круг обладает бесконечной симметрией, то есть его можно повернуть на любой угол без изменения вида фигуры.

Использование круга в повседневной жизни:

Круг является одной из наиболее распространенных геометрических фигур и находит широкое использование в различных сферах нашей жизни. Например, круг используется в качестве основы для монет, самолетных шин, колес, тарелок и многих других предметов. Круг также является одной из основных форм для создания картин и пространственных конструкций в искусстве и архитектуре.

Треугольник и его виды

Основные виды треугольников:

1. Равносторонний треугольник — это треугольник, у которого все три стороны и все три угла равны между собой. Каждый угол равен 60 градусам.

2. Раннобедренный треугольник — это треугольник, у которого две стороны равны между собой, и два угла при основании равны между собой. Третий угол может быть разным.

3. Прямоугольный треугольник — это треугольник, у которого один из углов является прямым (равным 90 градусам).

4. Остроугольный треугольник — это треугольник, у которого все углы меньше 90 градусов.

5. Тупоугольный треугольник — это треугольник, у которого один из углов больше 90 градусов.

6. Разносторонний треугольник — это треугольник, у которого все три стороны разные.

Треугольник является одной из самых простых и распространенных геометрических фигур. Знание основных видов треугольников позволяет более глубоко изучать геометрию и применять ее знания в решении задач и построении различных конструкций.

Овал или эллипс — красивая и плавная форма

Овалы и эллипсы используются в различных областях нашей жизни. Часто их можно увидеть в дизайне интерьера и архитектурных решениях. Овалы используются для создания оконных и дверных проемов, а также для придания оригинальности мебели.

Овал и эллипс в искусстве

Овал и эллипс также широко используются в искусстве. Многие художники используют эти формы для создания гармоничных и привлекательных композиций. Овальные формы часто встречаются в портретах, где они придают изображению мягкость и эстетическую привлекательность.

Символическое значение овала

Овал также имеет символическое значение. В многих культурах овал считается символом спокойствия и гармонии. Эта форма ассоциируется с женственностью и красотой.

Важно отметить, что овал и эллипс — не одно и то же. Овал имеет две равные оси, а эллипс — две неравные оси.

Параллелограмм — фигура с прямыми сторонами

У параллелограмма есть несколько основных свойств:

1. Противоположные стороны параллельны и равны.

Это означает, что если взять две противоположные стороны параллелограмма и продолжить их, то они никогда не пересекутся и будут иметь одинаковую длину.

2. Противоположные углы также равны.

Это значит, что если взять две противоположные стороны параллелограмма и продолжить их до их пересечения, то образующийся угол будет иметь такую же меру, как и его противоположный угол.

Параллелограмм широко используется в математике и геометрии, так как многие другие геометрические фигуры могут быть представлены как параллелограммы с дополнительными условиями. Например, прямоугольник — это особый случай параллелограмма, у которого все углы прямые.

Свойство	Описание
Противоположные стороны	Параллельны и равны
Противоположные углы	Равны
Сумма углов	Всегда равна 360 градусов

Таким образом, параллелограмм — это геометрическая фигура с прямыми сторонами, противоположные стороны которой параллельны и равны, а противоположные углы равны. Это одна из основных фигур, используемых при изучении геометрии и ее применении в практических задачах.

Трапеция — фигура с двумя параллельными сторонами

Кроме оснований, у трапеции есть еще две боковые стороны, которые не параллельны друг другу. Они соединяют основания и называются боковыми сторонами трапеции. Боковые стороны обычно обозначаются буквами c и d.

Также у трапеции существует два угла, которые находятся между основаниями. Они называются вершинами трапеции и обычно обозначаются буквами A и B. Угол A располагается у основания a, а угол B — у основания b.