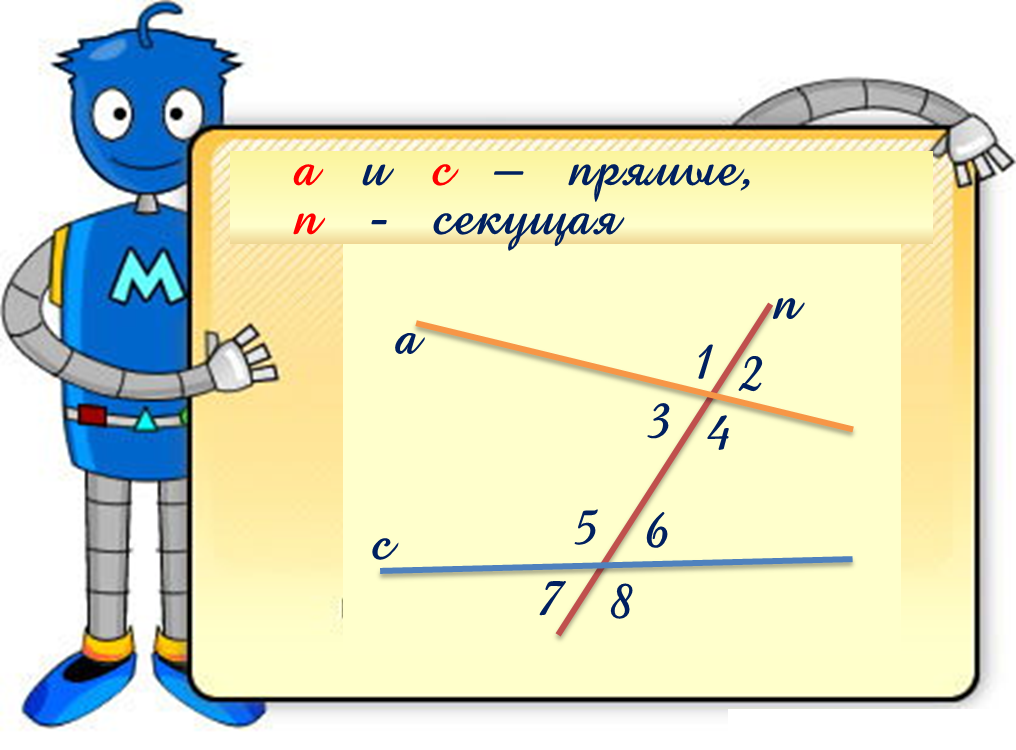
При пересечении двух прямых образуются различные углы, которые имеют свои уникальные названия и свойства. Рассмотрим основные виды углов, которые возникают при пересечении прямых.
Первый вид углов — вертикальные углы. Они образуются четырьмя прямыми линиями, две из которых пересекаются. Вертикальные углы равны друг другу и могут быть как остроугольными, так и тупоугольными.
Еще один вид углов — смежные углы. Они образуются двумя прямыми линиями, которые пересекаются, и имеют общую вершину. Смежные углы дополняют друг друга до 180 градусов и всегда равны. Они могут быть как остроугольными, так и тупоугольными.
Кроме вертикальных и смежных углов, существуют также замещающие углы. Они образуются двумя параллельными прямыми линиями и пересекаются третьей прямой. Замещающие углы равны друг другу и всегда являются парой одновременно остроугольных или тупоугольных углов.
Изучение углов при пересечении двух прямых является важной темой в геометрии. Понимание их свойств помогает решать задачи и строить различные фигуры. Знание названий и особенностей углов позволяет точно описывать их характеристики и взаимное расположение.
История и определение углов при пересечении двух прямых
Угол — это область плоскости, заключенная между двумя лучами, исходящими из одной точки, называемой вершиной угла. При пересечении двух прямых образуется несколько разных типов углов.
Одним из наиболее распространенных типов углов при пересечении двух прямых является прямой угол. Этот угол составляет 180 градусов и образуется, когда две прямые пересекаются, образуя прямую линию.
Другим важным типом углов является вертикальный угол. Вертикальные углы образуются, когда две прямые пересекаются так, что противоположные углы равны между собой.
Существует также множество других типов углов при пересечении двух прямых, таких как острые углы, тупые углы, смежные углы и другие. Каждый из них имеет свои характеристики и свойства, которые изучаются в геометрии и применяются при решении различных задач.
Изучение углов при пересечении двух прямых является важным элементом развития математического мышления и способствует пониманию геометрических форм и отношений. Они также широко применяются в различных областях, таких как архитектура, инженерное дело, компьютерная графика и дизайн.
Прямоугольный угол как основной тип угла при пересечении двух прямых
Углы при пересечении двух прямых можно классифицировать по типу. Один из основных типов углов, которые образуются при пересечении двух прямых, называется прямоугольным углом.
Определение
Прямоугольный угол образуется, когда две прямые пересекаются и одна из параллельных сторон образует прямой угол с пересекающей прямой. Внешний вид такого угла напоминает букву «L».
Свойства

Прямоугольный угол равен 90 градусам или π/2 радианам.
Сумма всех углов вокруг точки, включая прямоугольный угол, составляет 360 градусов или 2π радианов.
Прямоугольный угол является основой для многих других типов углов, таких как острый угол и тупой угол.
Использование
Прямоугольные углы широко используются в геометрии, архитектуре, инженерии и других областях. Они особенно полезны для создания прямых линий и перпендикулярных связей между объектами.
Особенности острого угла при пересечении двух прямых
1. Расположение острого угла
Острый угол образуется между двумя полуплоскостями, которые ограничены пересекающимися прямыми. При пересечении прямых образуется точка пересечения, а острый угол располагается между линиями, определяющими эти полуплоскости.
2. Свойства острого угла
Острый угол имеет несколько свойств, которые можно использовать для его изучения:
- Острый угол является описанным углом, то есть он может быть описан окружностью.
- Острый угол всегда меньше прямого угла (равного 90 градусам).
- Острый угол может быть равносторонним или неравносторонним, в зависимости от расположения пересекающихся прямых.
Знание особенностей острого угла при пересечении двух прямых поможет лучше понять и анализировать геометрические задачи и конструкции, связанные с пересечением прямых.
Свойства тупого угла при пересечении двух прямых
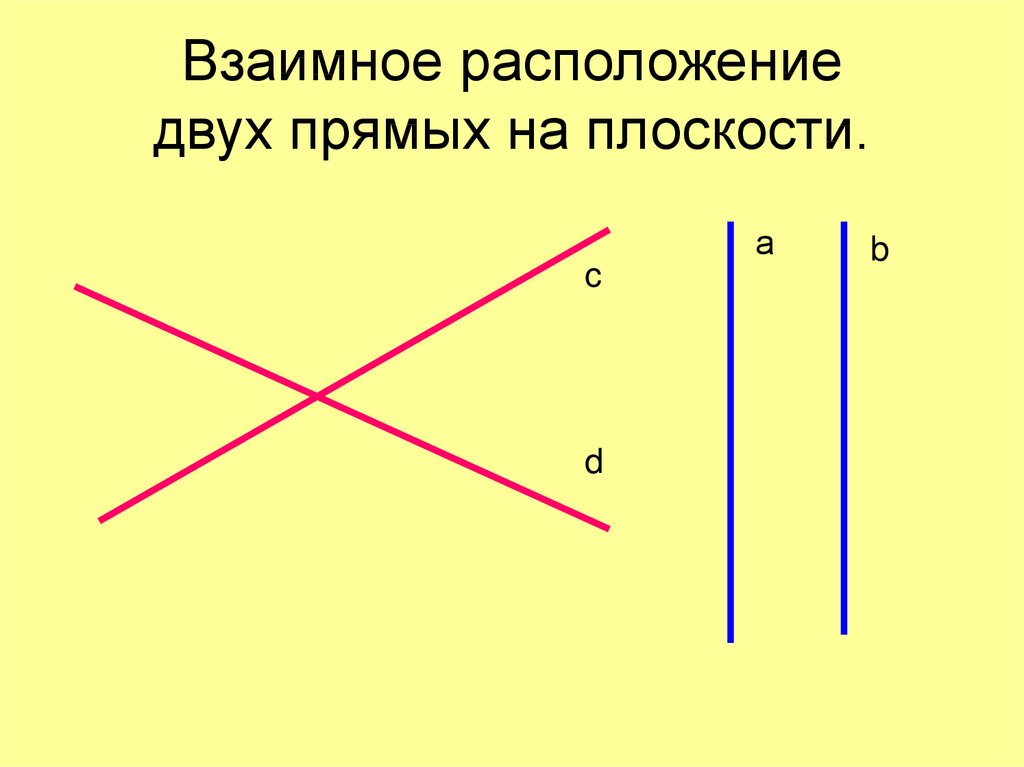
Свойства тупого угла при пересечении двух прямых:
- Тупой угол всегда меньше 180 градусов. Он не может быть равен или больше прямого угла (180 градусов).
- Тупой угол всегда острее правого угла (90 градусов) и туплее острого угла (меньше 90 градусов).
- Сумма всех углов, образованных при пересечении двух прямых, всегда равна 360 градусов. Поэтому, если один угол является тупым, остальные углы должны быть острыми.
- Тупой угол может быть определен как сумма двух смежных острых углов при пересечении двух прямых.
Свойства тупых углов при пересечении двух прямых играют важную роль в геометрии и могут быть использованы для решения различных задач и построений.
Угла безразмерность и его особенности при пересечении двух прямых
Во-первых, углы при пересечении двух прямых могут быть различных типов: острым, тупым или прямым. Острый угол имеет меньшую меру, чем прямой (равную 90 градусам), тупой угол имеет большую меру, чем прямой, а прямой угол равен 90 градусам.
Во-вторых, углы при пересечении двух прямых могут быть вертикальными, смежными или накрест. Вертикальные углы образуются при пересечении двух прямых и равны друг другу. Смежные углы лежат рядом друг с другом и их сумма составляет 180 градусов. Углы накрест располагаются на противоположных сторонах пересечения и их сумма также равна 180 градусов.
Кроме того, углы при пересечении двух прямых могут быть взаимно дополнительными или дополнительными. Взаимно дополнительные углы имеют сумму, равную 90 градусам, а дополнительные углы имеют сумму, равную 180 градусам.
Интересно отметить, что углы при пересечении двух прямых являются безразмерными величинами, то есть они не имеют единицы измерения. Однако, они могут быть измерены в градусах, минутах и секундах, или в радианах.
Также стоит упомянуть, что углы при пересечении двух прямых могут служить основой для различных геометрических конструкций, таких как построение параллельных прямых, нахождение высоты треугольника и других.
Нахождение и измерение невыпуклых углов при пересечении двух прямых
При пересечении двух прямых образуются углы, которые могут быть выпуклыми (меньше 180 градусов) или невыпуклыми (больше 180 градусов). Невыпуклые углы характеризуются тем, что их внутренний угол больше прямого угла (180 градусов) и они направлены в обратную сторону.
Чтобы найти невыпуклый угол при пересечении двух прямых, необходимо:
- Установить точку пересечения двух прямых.
- Провести прямую через точку пересечения, параллельную одной из прямых.
- Найти точку, в которой эта параллельная прямая пересекает вторую прямую.
- Измерить угол, образованный этими двумя прямыми.
Чтобы измерить невыпуклый угол, можно использовать геометрические инструменты, такие как угломер или геодезический компас. Также можно использовать математические вычисления, если известны координаты точек на плоскости.
Невыпуклые углы имеют важное значение в различных областях, таких как геометрия, физика, инженерия и архитектура. Например, в архитектуре невыпуклые углы могут использоваться для создания интересных и оригинальных форм зданий.
Особенности выпуклого угла при пересечении двух прямых
Выпуклый угол образуется двумя отрезками прямых, которые пересекаются внешней стороной и направлены в разные стороны. Этот угол всегда является остроугольным, то есть его мера не превышает 90 градусов.
Основные особенности выпуклого угла при пересечении двух прямых:
- Выпуклый угол всегда имеет внешнюю область, которая находится снаружи угла и не содержит пересечения с углом. Внешняя область выпуклого угла может быть использована, например, для построения треугольников.
- Выпуклый угол может быть измерен с помощью специальных инструментов, таких как транспортир.
- Выпуклый угол можно классифицировать по его размеру. Если угол меньше 90 градусов, он называется остроугольным выпуклым углом. Если угол равен 90 градусов, он называется прямым выпуклым углом. Если угол больше 90 градусов, он называется тупоугольным вогнутым углом.
Выпуклые углы при пересечении двух прямых активно используются в геометрии, строительстве, а также в различных научных и технических областях. Получившиеся углы обладают рядом интересных свойств и используются для решения различных задач.
Малый угол и его свойства при пересечении двух прямых
Малый угол — это угол, который лежит между двумя прямыми и его величина меньше 90 градусов. Он может быть отрицательным, если направление измерения происходит в обратном порядке.
Из свойств малого угла при пересечении двух прямых можно выделить следующее:
| Свойство | Описание |
| 1. | Малый угол всегда лежит между двумя прямыми. Если прямые параллельны, то малый угол равен 0 градусам. |
| 2. | Угол может быть остроугольным (меньше 90 градусов) или тупоугольным (больше 90 градусов). |
| 3. | Малый угол всегда имеет свою величину, которая может быть выражена в градусах или радианах. |
| 4. | Малый угол обладает свойством симметрии: если поменять направление измерения, то величина угла останется той же, но знак изменится. |
Малый угол при пересечении двух прямых играет важную роль в геометрии и находит применение в различных областях науки и техники.
Линии при пересечении прямых и их виды
При пересечении двух прямых образуются особые линии, которые имеют свои названия и свойства.
1. Прямая пересечения — линия, которая проходит через точку пересечения двух прямых и задается уравнением пересечения. Она является общим решением системы уравнений двух прямых.
2. Параллельные линии — две прямые, которые не пересекаются, имеют одинаковое направление и расстояние между ними постоянно.
3. Секущая — прямая, которая пересекает две прямые в различных точках. Секущая может быть общей для нескольких прямых или иметь только одну точку пересечения.
4. Перпендикуляр — прямая, которая образует прямой угол с другой прямой.
5. Диагональ — прямая, которая соединяет две непримыкающие друг к другу вершины многоугольника.
Важно: при пересечении прямых возможны различные комбинации образования линий, в зависимости от углов и положения прямых относительно друг друга.
Чтобы правильно определить виды линий при пересечении прямых, необходимо анализировать их углы и коэффициенты наклона.
Вопрос-ответ:
Как называется угол при пересечении двух прямых?
Угол, образованный при пересечении двух прямых, называется углом пересечения.
Чем отличается угол пересечения от других углов?
Угол пересечения образуется только в случае пересечения двух прямых. Он может быть острым, прямым или тупым.
Есть ли угол пересечения только при пересечении двух прямых под прямым углом?
Нет, угол пересечения может образовываться при пересечении двух прямых под любым углом — острым, прямым или тупым.
Как называется угол пересечения, если прямые пересекаются под прямым углом?
Если две прямые пересекаются под прямым углом, угол пересечения называется прямым углом.
Можно ли измерить угол пересечения двух прямых?
Да, угол пересечения двух прямых может быть измерен с помощью инструментов для измерения углов, таких как геодезический лазер или угломер.