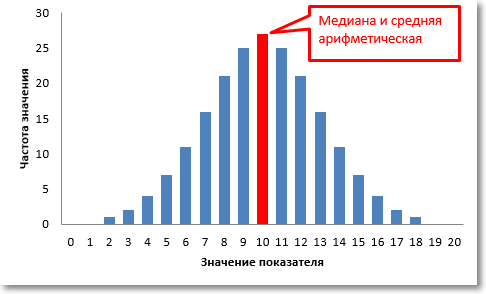
Медиана — это один из основных показателей в статистике, который играет важную роль при анализе данных. Она позволяет нам определить среднее значение в наборе чисел, учитывая их порядок. Медиана является устойчивой мерой центральной тенденции, которую используют для описания распределения данных.
Для того, чтобы вычислить медиану, необходимо упорядочить все числа по возрастанию или убыванию. Затем, если имеется нечетное количество чисел, медианой будет значение, которое находится посередине. Если же число значений четное, медианой будет среднее арифметическое двух центральных чисел.
Медиана используется в статистике вместе с другими показателями, такими как среднее значение и мода, для более полного описания данных. Она особенно полезна в случаях, когда имеется выброс или выборка несимметрична, поскольку медиана не чувствительна к экстремальным значениям и даёт нам более устойчивую оценку центрального значения набора данных.
Определение и значение медианы
Медиана является одним из методов описательной статистики, который позволяет определить «срединное» значение, игнорируя влияние экстремальных значений и выбросов. Поэтому она может быть более надежной мерой, чем среднее арифметическое, особенно в случаях, когда данные содержат аномалии или распределены неоднородно.
Значение медианы можно рассчитать, упорядочив данные по возрастанию и выбрав серединное значение. Если в наборе данных нечетное количество значений, медиана будет представлена центральным значением. Если количество значений четное, медиана будет равна среднему арифметическому двух центральных значений.
Одним из основных преимуществ медианы является то, что она чувствительна к порядку, но не чувствительна к масштабу данных. Следовательно, медиана позволяет получить представление о центральной тенденции данных, не учитывая возможные ошибки измерения или крайних значений.
Медиана широко используется во многих областях, включая экономику, социологию, медицину и многие другие, где необходимо анализировать распределение данных и оценивать среднее значение, но учитывать влияние выбросов.
Понятие медианы в статистике
Медиана является более устойчивой мерой центральной тенденции по сравнению с средним значением (среднее арифметическое). Она не зависит от выбросов в данных и характеризует середину набора значений.
Для вычисления медианы, данные должны быть упорядочены по возрастанию или убыванию. Если количество значений в наборе четное, медиана определяется как среднее арифметическое двух средних значений. Если количество значений в наборе нечетное, медианой считается значение, которое занимает середину в упорядоченном наборе данных.
Медиана наиболее полезна при анализе данных, которые имеют выбросы или отклонения от нормального распределения. Она позволяет получить более точное представление о центральной тенденции данных, учитывая уникальные значения, которые могут сильно влиять на среднее значение.
В статистическом анализе медиана используется для характеристики центральной тенденции в различных областях, включая экономику, медицину, социологию и многие другие. Она помогает исследователям понять, где находится середина данных, и какие значения считать типичными или нормальными.
Значение медианы для анализа данных
Медиана особенно полезна в случаях, когда среднее арифметическое (среднее значение) может быть искажено тяжелыми выбросами или неравномерным распределением данных. Медиана устойчива к экстремальным значениям и отражает «типичное» значение в наборе данных.
Когда набор данных имеет нечетное количество значений, медиана будет точным значением в середине упорядоченной последовательности. Если количество значений четное, медиана вычисляется как среднее арифметическое двух значений в середине.
Пример:
Допустим, у нас есть следующий набор данных: 3, 4, 5, 6, 12, 15, 18. В данном случае, количество значений равно 7, что является нечетным числом. Следовательно, медиана будет являться 4-м элементом в упорядоченной последовательности, то есть 6.
Как вычисляется медиана
- Отсортировать набор чисел по возрастанию или убыванию.
- Если количество чисел в наборе нечетное, медианой будет значение, находящееся в середине массива. Например, в наборе чисел [1, 2, 3, 4, 5] медианой будет число 3.
- Если количество чисел в наборе четное, медиана будет средним значением двух чисел, находящихся в середине. Например, в наборе чисел [1, 2, 3, 4, 5, 6] медианой будет среднее значение 3 и 4, то есть 3.5.
Вычисление медианы является одним из методов центральной тенденции и позволяет найти «среднее» значение в наборе данных. Этот показатель особенно полезен, когда имеется выбросы или аномалии в данных, так как медиана устойчива к экстремальным значениям.
Шаги для вычисления медианы
Для вычисления медианы, следуйте следующим шагам:
- Упорядочите набор данных по возрастанию или убыванию.
- Определите количество элементов в наборе данных.
- Если количество элементов нечетное, найдите значение, которое находится посередине упорядоченного набора данных.
- Если количество элементов четное, возьмите два значения, которые находятся посередине упорядоченного набора данных, и возьмите их среднее значение.
Полученное значение является медианой набора данных и представляет собой центральное значение, разделяющее набор пополам.
Например, для набора данных {1, 2, 3, 4, 5}, после упорядочивания получим {1, 2, 3, 4, 5}. Определение количества элементов — 5. Так как количество элементов нечетное, медианой будет значение 3.
Данный алгоритм применим для каких-либо числовых данных, таких как возраст, зарплата, оценки и т. д.
| Упорядоченный набор данных | Количество элементов | Медиана |
|---|---|---|
| 1, 2, 4, 5, 6, 7 | 6 | 4 |
| 2, 4, 6, 8, 10, 12, 14, 16, 18, 20 | 10 | 11 |
Пример вычисления медианы
Для наглядной демонстрации работы с медианой в статистике, представим следующий набор данных: 5, 7, 2, 9, 4, 6, 1.
Сначала отсортируем этот набор данных в порядке возрастания: 1, 2, 4, 5, 6, 7, 9.
Теперь вычислим значение медианы. В данном случае набор данных состоит из 7 элементов, поэтому медианой будет значение, которое находится посередине после сортировки. В нашем случае это число 5.
Таким образом, медиана этого набора данных равна 5.
Применение медианы в практических задачах
Один из способов использования медианы – в оценке центральной тенденции данных. В отличие от среднего арифметического, который подвержен воздействию выбросов, медиана не чувствительна к экстремальным значениям и представляет собой середину упорядоченного ряда данных. Это делает ее полезной для описания среднего значения в распределении с асимметричной формой или наличием выбросов.
Другая практическая область использования медианы – в медицине. Например, при анализе результатов клинических испытаний нового лекарства, медиана может дать представление о средней продолжительности выживаемости пациентов. Также медиана может использоваться при изучении эффективности лечения и оценке доли пациентов, достигших определенного уровня ответа на лечение.
В экономике и финансах медиана применяется для измерения доходности, инфляции и других показателей. Она помогает исключить экстремальные значения и уловить средние показатели, что особенно важно при проведении анализа рисков и определении стратегий вложений.
Другие сферы применения медианы включают демографию, социологию, психологию и маркетинг. Медиана может быть полезной в определении типичного представителя выборки или среднего значения для определенной группы людей или потребителей.
Таким образом, медиана широко используется в практических задачах, где центральная тенденция данных является важным показателем. Она позволяет учесть особенности распределения и предоставляет более устойчивую меру сравнения, в отличие от среднего арифметического.
Использование медианы для описания центральной тенденции
Использование медианы для описания центральной тенденции имеет свои преимущества. Во-первых, медиана устойчива к выбросам и экстремальным значениям, поэтому она может быть полезна в случаях, когда данные имеют необычные значения, которые могут исказить среднее значение. Во-вторых, медиана позволяет получить представление о типичном значении в наборе данных, так как она разделяет данные пополам.
Использование медианы особенно полезно в случаях, когда данных мало или они распределены неравномерно. Например, если у нас есть информация о зарплатах в неком предприятии, и большинство сотрудников имеют низкую зарплату, но несколько человек получают очень высокую зарплату, то среднее значение может быть сильно искажено этими крайними значениями. В такой ситуации медиана может предоставить более объективную оценку типичной зарплаты на предприятии.
Таким образом, использование медианы для описания центральной тенденции позволяет получить более устойчивую и объективную оценку значений в наборе данных. Этот показатель особенно полезен в случаях, когда данные имеют выбросы или имеют неравномерное распределение.
Вопрос-ответ:
Что такое медиана и зачем она нужна в статистике?
Медиана — это значение, которое делит упорядоченный набор данных на две равные части. Она позволяет нам оценить центральную тенденцию распределения и играет важную роль при анализе статистических данных, особенно в случаях, когда имеются выбросы или скошенное распределение.
Как найти медиану в статистике?
Для нахождения медианы, необходимо упорядочить рассматриваемый набор данных по возрастанию или убыванию и найти значение, которое находится в середине этого упорядоченного набора. Если количество данных нечетное, медиана — это значение, находящееся точно в середине. Если количество данных четное, медианой считается среднее арифметическое двух средних значений.
Что делать, если у меня есть выбросы в данных?
Если у вас есть выбросы в данных, медиана становится более робастной статистикой, чем среднее значение. Она нечувствительна к экстремальным значениям и лучше представляет «типичное» значение. Поэтому, использование медианы вместо среднего значение может быть более предпочтительным, когда данные содержат выбросы.
Какое значение имеет медиана, если данные имеют скошенное распределение?
Если данные имеют скошенное распределение, медиана будет отличаться от среднего значения. В случае, когда распределение данных смещено вправо (положительное скошенное), медиана будет меньше среднего значения. Если данные смещены влево (отрицательное скошенное), медиана будет больше среднего значения. Таким образом, медиана является более устойчивой оценкой центральной тенденции в случае скошенного распределения.