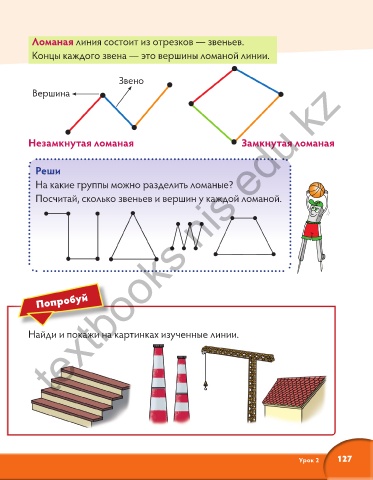
Ломаная – это геометрическая фигура, состоящая из отрезков, соединяющих вершины. Каждая вершина является точкой пересечения двух отрезков. Звенья ломаной – это отрезки, которые соединяют соседние вершины. Длина ломаной определяется суммой длин всех ее звеньев.
Ломаная с восьмью звеньями – это особый случай ломаной, состоящий из восьми отрезков и девяти вершин. Такая ломаная имеет сложную и интересную структуру. Восьмиугольник является одной из самых простых и популярных форм для ломаной с восьмью звеньями.
Ломанная: определение, структура и свойства
Структура ломаной определяется порядком вершин, а также расположением и направлением звеньев. Ломаная с заданным порядком вершин образует замкнутую либо незамкнутую геометрическую фигуру. Замкнутая ломаная имеет первую и последнюю вершину, соединенные между собой, что создает замкнутый контур. Замкнутая ломаная образует, например, многоугольник.
Свойства ломаной зависят от ее структуры. Длина ломаной определяется суммой длин всех ее звеньев. Угол между двумя звеньями ломаной может быть разным, включая 180 градусов (если звенья ломаной лежат на одной прямой).
Ломаная может быть правильной или неправильной. Правильная ломаная — это ломаная, у которой все звенья равны по длине, а углы между звеньями равны. Неправильная ломаная имеет звенья и углы разной длины и различные углы между звеньями.
Ломаная является важным элементом в геометрии. Она используется для построения различных фигур и моделей, а также в анализе и описании форм и структур. Понимание определения, структуры и свойств ломаной позволяет решать задачи, связанные с этим геометрическим объектом.
Что такое ломаная?
Ломаная полезна для визуализации и анализа данных в различных областях, включая математику, физику, компьютерную графику и статистику. Она позволяет представить изменение величины или показателя в течение времени или других параметров.
Для определения ломаной необходимо знать координаты точек, которые нужно соединить. Координаты точек обычно представлены в декартовой системе координат, где каждая точка определяется парой чисел (x, y). Соединяя последовательные точки отрезками, получаем ломаную.
Длина ломаной вычисляется как сумма длин всех ее отрезков. Для этого можно использовать теорему Пифагора или модуль разности координат точек.
Ломаная может иметь различные формы и законы изменения координат точек. Она может быть прямой, изогнутой, состоять из сегментов с различным уклоном и т.д. Направление и форма ломаной зависят от расположения точек относительно друг друга.
| Пример ломаной: |
|---|
(1, 1) (3, 5) (5, 2) \ / \ / \ / \ / \ / \ / \ / \ / \/ \/ |
В данном примере ломаная состоит из трех отрезков и является открытой, так как начало и конец отрезков не соединяются. Она бежит по точкам (1, 1), (3, 5) и (5, 2).
Ломаная может использоваться для отображения траектории движения объекта, графика функции или просто для связи точек на плоскости. Она помогает визуализировать и анализировать данные и является важным инструментом визуального представления информации.
Определение понятия ломаная
Ломаная может быть составлена из произвольного числа звеньев и иметь различную форму. Вершины ломаной обычно обозначаются буквами, например, A, B, C, и т.д. Длина каждого звена важна для определения формы и свойств ломаной.
Для определения формы ломаной используется понятие углов звеньев. Угол между двумя звеньями определяется как угол, образованный ими при пересечении в точке вершины. Углы звеньев могут быть разнообразными и варьироваться от острых до прямых и тупых.
Длина ломаной определяется суммой длин всех ее звеньев. В зависимости от длины и формы ломаных, они могут иметь различные свойства, такие как выпуклость или вогнутость.
Ломаные широко используются в различных областях, таких как графика, картография, а также в математике и физике для аппроксимации кривых.
Примеры использования ломаных
- В графике и дизайне: ломаные линии применяются для создания различных путей движения, контуров или контрольных точек. Они помогают создать интересные и динамичные композиции.
- В картографии: ломаные используются для обозначения границ, дорог и других элементов на карте. Также они помогают показать направление движения.
- В математике: ломаные применяются для аппроксимации кривых, моделирования и анализа данных. Например, они часто используются при построении графиков.
- В программировании: ломаные могут быть использованы для реализации алгоритмов движения или отслеживания позиции объектов.
Примеры использования ломаных не ограничиваются этими областями — они могут быть применены в любой ситуации, где требуется создание делительной линии или простого пути соединения точек.
Структура ломаной
Длина ломаной является суммой длин всех звеньев, которые ее составляют. Длина звена – это евклидово расстояние между двумя соседними вершинами. Чем больше звеньев содержит ломаная, тем более сложную структуру имеет данная фигура.
Структура ломаной может быть прямолинейной или изогнутой. В случае прямолинейной структуры все звенья ломаной являются отрезками прямых линий и не пересекаются друг с другом. В случае изогнутой структуры звенья имеют форму дуги и могут пересекаться между собой.
Звенья ломаной могут иметь разные величины и направления. Величина звена определяет его длину, а направление – угол отклонения от предыдущего звена. При изменении величины или направления звенья меняется и структура ломаной.
Изучение структуры ломаной позволяет определить ее свойства, такие как выпуклость, замкнутость, симметричность и т.д. Это полезно, например, при создании компьютерной графики, алгоритмов пути и многих других задачах.
Основные элементы ломаной
Основными элементами ломаной являются:
- Вершины: точки, которые соединяют звенья ломаной. Каждая вершина имеет свои координаты и порядковый номер.
- Звенья: отрезки, соединяющие вершины между собой. Каждое звено определяется начальной и конечной вершинами.
- Длина: сумма длин всех звеньев. Длина ломаной выражается в единицах измерения, таких как пиксели, сантиметры или дюймы.
Ломаная может быть открытой или замкнутой. В открытой ломаной последний отрезок не соединяет вершину с первой, а в замкнутой ломаной первая и последняя вершины соединены последним звеном.
Основные элементы ломаной определяют ее форму, структуру и свойства. Они являются основой для проведения различных геометрических операций и расчетов.
Правильная и неправильная ломаные
Правильная ломаная – это ломаная, у которой все звенья имеют равную длину. Такая ломаная образует замкнутую фигуру, которая может быть регулярным многоугольником. Например, правильной ломаной является правильный треугольник или квадрат.
Неправильная ломаная – это ломаная, у которой звенья имеют разную длину. Такие ломаные могут образовывать сложные фигуры, причем достаточно изменить длину одного звена, чтобы существенно изменить форму ломаной. Например, неправильной ломаной может быть кривая спираль или замкнутый контур объекта.
Правильные и неправильные ломаные находят свое применение в различных областях, включая геометрию, графику и дизайн. Они используются для создания изогнутых линий, украшений, плоских фигур и многое другое. Изучение закономерностей и свойств правильных и неправильных ломаных позволяет лучше понять их структуру и применение.
Свойства ломаной
1. Вершины ломаной. Вершинами ломаной являются точки, в которых отрезки соединяются друг с другом. Существует одна особая вершина, называемая начальной вершиной, и одна конечная вершина, между которыми протягиваются отрезки ломаной.
2. Отрезки ломаной. Ломаная состоит из отрезков, которые соединяют вершины. Длина отрезков может быть различной и зависит от данной ломаной.
3. Длина ломаной. Длина ломаной определяется как сумма длин всех отрезков, составляющих её. Чтобы найти длину ломаной, нужно просуммировать длины всех её отрезков.
4. Повороты ломаной. Ломаная может иметь повороты, то есть изменения направления отрезков. Повороты могут быть различных типов: острый поворот, прямой поворот или тупой поворот. Эти повороты важны при изучении свойств и качеств ломаной.
Ломаная является важной геометрической фигурой, используемой в различных областях, таких как математика, физика, компьютерная графика и т.д. Понимание её свойств и характеристик поможет в решении задач и построении графиков.
Длина ломаной
Для рассчета длины ломаной необходимо знать координаты вершин, через которые проходит линия. Длина ломаной рассчитывается как сумма длин всех сегментов, то есть расстояния между каждой парой соседних вершин.
Существует несколько способов определения длины ломаной в зависимости от ее типа и представления:
- Для простой (не самопересекающейся) ломаной, лежащей в одной плоскости, длина рассчитывается как сумма расстояний между соседними вершинами. Формула для данного случая будет выглядеть следующим образом:
d = ∑│Pi+1 - Pi│, где d — длина ломаной, а │Pi+1 — Pi│ — расстояние между вершинами Pi+1 и Pi. - Для самопересекающейся ломаной, длина рассчитывается аналогично, но с учетом наличия самопересечений. В данном случае, длина сегментов, пересекающих друг друга, учитывается по отдельности.
Зная длину ломаной, можно проводить различные анализы и операции над ней, такие как поиск кратчайшего пути или определение пересечений с другими ломаными.
Вопрос-ответ:
Что такое ломаная звенья вершины и длина 8?
Ломаная звенья вершины и длина 8 — это графическое представление ломаной линии, состоящей из 8 звеньев, которые могут быть соединены вершинами.
Насколько сложна построение ломаной с 8 звеньями?
Построение ломаной с 8 звеньями может быть сложным, так как требует определения точного расположения каждой вершины и соединения их звеньями. Однако, с помощью графических инструментов и правильного подхода, построение ломаной становится более простым.
Как использовать ломаную звенья вершины и длина 8 в графическом дизайне?
Ломаная звенья вершины и длина 8 может использоваться в графическом дизайне для создания различных форм и композиций. Это может быть полезным при создании абстрактных и геометрических паттернов, а также при организации элементов дизайна в узорах или картах.
Какова математическая природа ломаной звенья вершины и длина 8?
Математическая природа ломаной звенья вершины и длина 8 связана с геометрией и теорией графов. Ломаная является последовательностью звеньев, соединенных вершинами, и может быть изучена с помощью алгоритмов и методов теории графов. Длина 8 указывает на количество звеньев в ломаной и может влиять на ее форму и связности.