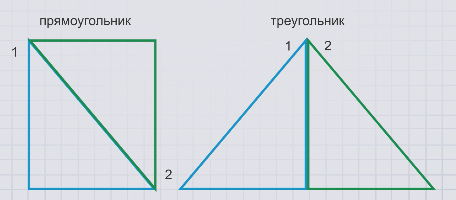
Математика всегда была учебным предметом, который вызывал множество вопросов учеников. Один из них связан с понятием равновеликих и равносоставленных многоугольников. Но что они означают?
Равновеликие многоугольники — это фигуры, которые имеют одинаковую площадь. Другими словами, если мы возьмем два многоугольника и сможем расположить их так, чтобы они полностью перекрылись, то их площади будут равными. При этом, формы и размеры многоугольников могут быть совершенно разными.
Равносоставленные многоугольники — это фигуры, у которых соответствующие стороны и углы равны. Если взять два равносоставленных многоугольника и приложить один к другому, то они будут полностью совпадать. То есть, их формы и размеры будут абсолютно идентичными.
Понимание этих понятий является важным для решения геометрических задач и построения фигур. Знание, что равновеликие многоугольники могут иметь разные формы, позволяет находить несколько решений для задач, а понятие равносоставленных многоугольников позволяет строить точные копии фигур.
Равновеликие и равносоставленные многоугольники
Для того чтобы определить, являются ли многоугольники равновеликими, можно применить несколько способов. Один из них — это сравнение соотношений длин сторон. Если соответствующие стороны двух многоугольников пропорциональны, то они равновеликие.
Равносоставленные многоугольники — это такие многоугольники, у которых соответствующие углы равны, а соответствующие стороны не обязательно пропорциональны. То есть, равносоставленные многоугольники имеют одинаковые углы, но могут иметь различную форму и длину сторон.
Для нахождения равносоставленных многоугольников можно использовать различные методы. Например, можно сравнивать соотношения длин сторон с помощью измерительных инструментов, таких как линейка или шаблон, либо применять математические формулы и теоремы для вычисления углов и сторон.
Изучение равновеликих и равносоставленных многоугольников имеет важное значение в геометрии, так как позволяет различать и классифицировать различные фигуры и вычислять их свойства. Эти понятия применяются при решении задач, связанных с подобием, измерением площадей и углов, а также в строительстве, архитектуре и других областях.
Определение и различия
- Равновеликий многоугольник — это многоугольник, у которого площади всех своих граней равны друг другу. То есть, если в многоугольнике есть, например, три треугольника, то все три треугольника должны иметь одинаковую площадь. Равновеликие многоугольники имеют одинаковую форму, но могут иметь разные размеры. Например, два равновеликих треугольника могут быть разных размеров, но будут иметь одинаковую форму и одинаковые площади своих граней.
- Равносоставленный многоугольник — это многоугольник, у которого углы и их порядок внутри фигуры совпадают, а соответствующие стороны пропорциональны. При этом фигуры могут иметь разные размеры. Например, два равносоставленных треугольника могут быть разных размеров, но иметь одинаковые углы и стороны, которые пропорциональны друг другу.
Таким образом, равновеликие и равносоставленные многоугольники имеют разные свойства и отличаются друг от друга. Понимание этих различий важно при решении геометрических задач и построении фигур.
Определение равновеликих многоугольников
Для определения равновеликости многоугольников необходимо сравнивать соответствующие стороны и углы каждого из многоугольников. Если все значения совпадают, то многоугольники являются равновеликими, в противном случае они разные.
Равновеликие многоугольники могут иметь разное количество сторон и разную форму, но при условии, что все соответствующие стороны и углы равны, они считаются равновеликими. Например, два треугольника с равными сторонами и равными углами будут равновеликими, несмотря на то, что форма может быть разной.
Определение равносоставленных многоугольников
Другими словами, равносоставленные многоугольники имеют одинаковую форму, но могут отличаться размером.
Для двух многоугольников считается, что они равносоставленные, если каждая сторона первого многоугольника соответствует по длине соответствующей стороне второго многоугольника, и каждый угол первого многоугольника равен соответствующему углу второго многоугольника.
Равносоставленные многоугольники могут иметь различное количество сторон и быть выпуклыми или невыпуклыми.
Такое определение позволяет нам сравнивать и классифицировать многоугольники на основе их формы, а не только размера.
Свойства и примеры
Равновеликие многоугольники: два многоугольника называются равновеликими, если они имеют равную площадь. Это значит, что все соответствующие стороны и углы многоугольников равны.
Равносоставленные многоугольники: два многоугольника называются равносоставленными, если они имеют равные углы. Это значит, что соответствующие углы многоугольников равны, но стороны могут быть разными.
Свойство равновеликих многоугольников позволяет утверждать, что если два многоугольника равновелики, то их площади равны, а значит, можно сравнивать их размеры. Например, если известны площади двух треугольников, то по сравнению этих площадей можно сказать, какой треугольник больше или меньше.
Свойство равносоставленных многоугольников позволяет утверждать, что если два многоугольника равносоставлены, то их углы равны. Это свойство часто применяется при решении геометрических задач, например, при нахождении неизвестных угловых величин.
Примеры равновеликих многоугольников:
— Равные прямоугольники: если два прямоугольника имеют одинаковые стороны, то они равновелики.
— Равносторонние треугольники: треугольники, у которых все стороны равны, являются равновеликими.
Примеры равносоставленных многоугольников:
— Квадраты: все углы квадрата равны, поэтому два квадрата могут быть равносоставленными, даже если их стороны различаются.
— Правильные шестиугольники: если шестиугольники имеют равные углы, то они равносоставленные, независимо от длин сторон.
Свойства равновеликих многоугольников
Свойства равновеликих многоугольников:
1. Стороны и углы: У равновеликих многоугольников все стороны равны по длине, а все углы равны по величине.
2. Площадь: Равновеликие многоугольники имеют одинаковую площадь, независимо от формы и размеров сторон.
3. Главные диагонали: Главные диагонали равновеликих многоугольников имеют одинаковую длину и пересекаются в их центре.
4. Периметр: У равновеликих многоугольников периметры совпадают, поскольку все стороны равны по длине.
5. Углы вписываемые и центральные: У равновеликих многоугольников соответствующие вписываемые и центральные углы равны.
6. Радиусы описанных окружностей: Равновеликие многоугольники имеют одинаковые радиусы описанных окружностей, которые касаются всех вершин многоугольника.
7. Высоты и медианы: Высоты и медианы равновеликих многоугольников имеют одинаковые длины.
Таким образом, равновеликие многоугольники обладают рядом свойств, которые делают их эквивалентными по площади и форме.
Свойства равносоставленных многоугольников
У равносоставленных многоугольников также есть несколько свойств:
| Свойство | Описание |
| 1. Равные стороны | У равносоставленных многоугольников длины соответствующих сторон равны. |
| 2. Равные углы | У равносоставленных многоугольников соответствующие углы равны. |
| 3. Равные периметры | Периметры равносоставленных многоугольников равны. |
| 4. Равные площади | Площади равносоставленных многоугольников равны. |
Равносоставленные многоугольники могут иметь разное количество сторон и форму, но будут иметь одинаковые свойства. Эти свойства позволяют нам сравнивать и классифицировать многоугольники и использовать их в различных геометрических задачах.
Практическое применение
Равновеликие и равносоставленные многоугольники широко используются в различных областях практической деятельности, включая геометрию, архитектуру, строительство и дизайн.
Эти многоугольники имеют четкие и одинаковые стороны и углы, что делает их полезными при решении геометрических задач. Они часто используются в математических моделях, при расчетах и в доказательствах теорем.
В архитектуре и строительстве равновеликие и равносоставленные многоугольники используются для создания красивых и гармоничных фасадов зданий. Они позволяют создавать симметричные формы, которые придают зданию особую эстетическую привлекательность.
Дизайнеры также активно применяют равновеликие и равносоставленные многоугольники в своей работе. Они используют их для создания графических композиций, узоров и орнаментов. Эти многоугольники могут дополнять друг друга или создавать симметричные узоры, добавляя глубину и интерес в дизайн.
В области компьютерной графики и анимации равновеликие и равносоставленные многоугольники играют важную роль. Они используются для создания 3D-моделей объектов и персонажей. Благодаря эффективному использованию этих многоугольников можно достичь высокой детализации и реалистичности визуальных эффектов.
Таким образом, равновеликие и равносоставленные многоугольники имеют широкое практическое применение в различных областях. Они помогают решать задачи и создавать эстетически привлекательные формы и композиции.
Вопрос-ответ:
Как определить равенство площадей двух многоугольников?
Для определения равенства площадей двух многоугольников необходимо сравнить их площади. Если они равны, то многоугольники называются равновеликими.
Что такое равносоставленные многоугольники?
Равносоставленные многоугольники – это многоугольники, у которых все соответствующие стороны пропорциональны.
Как найти площадь многоугольника?
Для нахождения площади многоугольника можно разделить его на треугольники и сложить площади этих треугольников.
Можно ли сказать, что равновеликие многоугольники всегда равносоставленные?
Нет, нельзя. Равновеликость многоугольников означает равенство их площадей, а равносоставленность – равенство всех соответствующих сторон. Таким образом, многоугольники могут быть равновеликими, но не равносоставленными и наоборот.
Какое значение имеет понятие равносоставленности многоугольников в геометрии?
Понятие равносоставленности многоугольников имеет большое значение в геометрии, так как позволяет установить соответствие между сторонами и углами двух или более многоугольников и сравнить их.
Чем отличаются равновеликие и равносоставленные многоугольники?
Равновеликие многоугольники имеют равные площади, но могут иметь различную форму, а равносоставленные многоугольники имеют одинаковое число сторон и соответствующие стороны равны по длине.