Биссектрисой треугольника называется вектор, который делит угол треугольника пополам. Она является важным элементом в геометрии и находит применение в различных задачах.
Свойства биссектрисы треугольника заслуживают особого внимания. Во-первых, они позволяют нам определить точку пересечения биссектрис треугольника, что является одним из ключевых моментов при решении задач на построение треугольников. Во-вторых, биссектриса треугольника делит противоположные стороны треугольника в отношении, равном отношению других двух сторон треугольника.
Например, если биссектриса треугольника делит сторону треугольника в отношении 1:2, то она делит другие две стороны в отношении 2:1. Это важное свойство биссектрисы позволяет нам находить все стороны треугольника, используя только одну из них и соответствующие биссектрисы.
Также следует отметить, что биссектрисы треугольника пересекаются в одной точке, которая называется центром биссектрис треугольника. Этот центр обладает рядом интересных свойств и является важной точкой, используемой в дальнейших рассуждениях геометрии треугольников.
Определение биссектрисы треугольника
Биссектрисой треугольника называется прямая, которая делит внутренний угол треугольника пополам. Вектор, соответствующий биссектрисе угла, можно определить с использованием геометрических вычислений.
Для того чтобы найти биссектрису треугольника, необходимо знать длины его сторон и углы. Предположим, что треугольник ABC имеет стороны a, b и c, а его углы противолежащие сторонам равны α, β и γ соответственно.
Для определения биссектрисы треугольника можно использовать следующие формулы:
| Биссектриса угла A: | ba = (c * cos(α/2) — b) / (cos(α/2) — cos(β + γ)/2) |
| Биссектриса угла B: | bb = (a * cos(β/2) — c) / (cos(β/2) — cos(α + γ)/2) |
| Биссектриса угла C: | bc = (b * cos(γ/2) — a) / (cos(γ/2) — cos(α + β)/2) |
Определение биссектрисы треугольника позволяет найти вектор, который делит угол треугольника пополам. Эта информация может быть полезна для решения различных геометрических задач и нахождения дополнительных свойств треугольника.
Биссектриса треугольника: понятие и обозначение
Обозначение биссектрисы обычно заключается в использовании буквы «b» с индексом, указывающим на номер угла треугольника. Например, b1 — обозначение биссектрисы первого угла треугольника.
Биссектриса треугольника является основным элементом исследования геометрии треугольников. Она проходит через вершину треугольника и делит угол пополам, создавая два новых угла, имеющих равную величину.
| Угол треугольника | Обозначение биссектрисы |
| Угол A | b1 |
| Угол B | b2 |
| Угол C | b3 |
Изучение биссектрис треугольника позволяет решать различные задачи, связанные с построением треугольников, нахождением их углов и сторон. Также биссектрисы используются в доказательствах теорем и свойств треугольников.
Зная понятие биссектрисы треугольника и ее обозначение, можно более глубоко изучать геометрию и решать задачи, связанные с этой темой.
Биссектриса треугольника: осуществление и свойства
Биссектрисой треугольника называется вектор, который делит угол треугольника пополам, то есть делит его на два равных угла.
Процесс нахождения биссектрисы треугольника зависит от типа задачи и может быть выполнен различными способами:
- Перпендикулярное построение: проведите перпендикуляр к стороне треугольника, проходящий через начало угла. Точка пересечения этого перпендикуляра с противоположной стороной будет являться началом биссектрисы.
- Разделение угла пополам: проведите луч из начала угла, который делит угол пополам. Точка пересечения этого луча с противоположной стороной будет являться началом биссектрисы.
- Аналитический метод: используйте координаты вершин треугольника и вычислите уравнение прямой, являющееся биссектрисой треугольника.
Биссектриса треугольника обладает следующими свойствами:
- Биссектрисы всех трех углов треугольника пересекаются в одной точке, называемой центром вписанной окружности.
- Биссектрисы ориентированы внутрь треугольника.
- Биссектриса каждого угла треугольника делит противолежащую сторону в соотношении, равном отношению длин двух других сторон треугольника, ориентированных относительно этого угла.
- Биссектриса одного угла треугольника является осью симметрии сектора, ограниченного этой биссектрисой и сторонами треугольника.
Механизм образования биссектрисы
Механизм образования биссектрисы основан на следующих идеях:
1. Взятие двух сторон треугольника: для нахождения биссектрисы угла треугольника необходимо взять две из его сторон, к которым этот угол относится. Именно эти две стороны будут использоваться для определения направления и величины биссектрисы.
2. Разделение одной из двух сторон треугольника на две части: для образования биссектрисы угла треугольника выбирается одна из двух сторон, к которой примыкает этот угол. Эта сторона разделяется на две части в отношении, обратном отношению двух других сторон треугольника, примыкающих к этому углу.
3. Направление и величина биссектрисы: полученные при разделении стороны точки служат началом и концом вектора биссектрисы угла треугольника. Направление вектора определяется от точки, лежащей ближе к основанию треугольника, к точке, лежащей ближе к вершине угла. Величина вектора определяется как половина длины разделенной стороны треугольника.
Таким образом, механизм образования биссектрисы треугольника основан на выборе сторон треугольника, разделении одной из них и задании направления и величины вектора, который делит угол пополам.
| Пример | Биссектриса |
|---|---|
 |  |
Биссектриса и углы треугольника
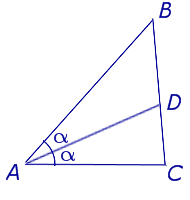
Рассмотрим треугольник ABC. Пусть AD — биссектриса угла A, BE — биссектриса угла B и CF — биссектриса угла C.
Биссектриса AD делит угол BAC на два равных угла — углы BAD и CAD. То есть, мера угла BAD равна мере угла CAD.
Аналогично, биссектриса BE делит угол ABC на два равных угла — углы ABE и CBE, а биссектриса CF делит угол ACB на два равных угла — углы ACF и BCF.
| Биссектриса | Угол | Углы, на которые делит |
|---|---|---|
| AD | Угол A | Угол BAD, угол CAD |
| BE | Угол B | Угол ABE, угол CBE |
| CF | Угол C | Угол ACF, угол BCF |
Таким образом, биссектрисы трех углов треугольника делят каждый угол пополам. Знание о биссектрисах углов треугольника позволяет решать различные задачи, связанные с построением треугольников и вычислением их углов и сторон.
Взаимоотношение биссектрисы с другими элементами треугольника
Биссектриса треугольника имеет важное взаимоотношение с другими его элементами, такими как стороны, углы и медианы.
Во-первых, биссектриса треугольника делит его угол пополам. Это означает, что она создает два равных угла, которые в сумме дают исходный угол. Также биссектриса является осью симметрии треугольника по отношению к этому углу.
Кроме того, биссектриса треугольника взаимно перпендикулярна медиане, проведенной из вершины этого угла. Это означает, что они образуют перпендикулярные линии, которые пересекаются в одной точке, называемой центром биссектрисы.
Биссектриса также связана со сторонами треугольника. Если разделить сторону, к которой она проведена, в отношении длин других сторон, то эти части стороны будут иметь одинаковые отношения к соседним сторонам.
Из этих взаимоотношений следует, что биссектриса является важным элементом треугольника, который помогает определить другие его характеристики и свойства.
Применение биссектрисы треугольника
Биссектриса треугольника может использоваться в различных геометрических задачах и конструкциях. Например, она помогает найти центр вписанной окружности треугольника. Для этого достаточно провести две биссектрисы треугольника и их пересечение будет являться центром вписанной окружности.
Также, биссектриса треугольника может быть использована для нахождения точек пересечения линий, проведенных из вершин треугольника и перпендикулярных его противоположным сторонам. Эти точки пересечения будут являться центрами вневписанных окружностей треугольника.
Биссектриса треугольника также может быть полезна при решении задач по нахождению длин сторон треугольника. Например, если известны длины двух сторон треугольника и угол между ними, то можно найти длину третьей стороны, используя биссектрису этого угла.
Таким образом, знание и применение биссектрисы треугольника позволяет решать разнообразные геометрические задачи и конструкции, делая ее важным инструментом в изучении и применении треугольников.
Решение задач по биссектрисе треугольника
Решение задач, связанных с биссектрисой треугольника, можно осуществить, используя свойства биссектрисы и знания о треугольниках.
Для начала, стоит вспомнить, что биссектриса треугольника делит его угол пополам. Это означает, что биссектриса делит противоположную сторону треугольника на две части в пропорции между собой, равной отношению других двух сторон треугольника.
Используя это свойство, можно решать различные задачи. Например, задачи на нахождение длины биссектрисы, задачи на нахождение длины стороны треугольника, если известны длины двух других сторон и длина биссектрисы, или задачи на нахождение площади треугольника, если известны длины сторон и длина биссектрисы.
Для решения таких задач можно использовать различные формулы и теоремы, такие как теорема синусов, теорема косинусов, формула Герона и другие. В каждой конкретной задаче нужно выбрать подходящую формулу и подставить известные данные для нахождения искомой величины.
В случае, если нужно решить задачу на построение биссектрисы треугольника, можно воспользоваться различными геометрическими построениями, такими как построение окружности, углов и отрезков. Например, для построения биссектрисы угла можно провести две окружности, касающиеся сторон угла, и провести пересекающиеся отрезки, соединяющие центры окружностей с точкой пересечения.
Важно также помнить, что биссектрисы треугольника, как и другие его элементы, могут обладать некоторыми свойствами, например, при пересечении внутренних биссектрис треугольника получается точка вписанной окружности, или при пересечении двух внешних биссектрис получается точка вневписанной окружности.
Задачи по биссектрисе треугольника могут быть различной сложности, но в основе их решения всегда лежат основные свойства и формулы, которые следует знать и уметь применять. Поэтому важно основательно изучить данную тему и научиться применять полученные знания на практике.
Вопрос-ответ:
Как определить биссектрису треугольника?
Биссектриса треугольника может быть определена как вектор, который делит угол треугольника пополам.
Что такое биссектриса угла треугольника?
Биссектрисой угла треугольника называется вектор, который делит данный угол на две равные части.
Как построить биссектрису треугольника?
Чтобы построить биссектрису треугольника, необходимо провести линию, которая делит угол треугольника пополам.
Зачем нужна биссектриса треугольника?
Биссектриса треугольника используется для нахождения точки пересечения биссектрис треугольника, которая называется центром вписанной окружности треугольника.