
Углы — это один из фундаментальных элементов геометрии, они представляют собой области, ограниченные двумя лучами, исходящими из одной точки. В геометрии существует множество различных типов углов, каждый из которых имеет свои особенности.
Один из наиболее интересных типов углов — это центральные углы. Центральный угол — это угол, вершина которого находится в центре окружности, а его стороны проходят через точки на окружности. Такой угол получает свое название из-за своего расположения — в центре.
Важной особенностью центрального угла является то, что его мера равна длине соответствующей дуги на окружности. То есть, если мы измерим центральный угол в градусах или радианах, то получим точное значение длины дуги, ограниченной этим углом на окружности.
Угол в геометрии
Одним из основных свойств угла является его мера, которая измеряется в градусах или радианах. Градусы — это единица измерения углов, принятая в системе градусов. Радианы — это другая единица измерения углов, используемая в математике и физике.
Существует несколько разновидностей углов, таких как прямой угол, острый угол, тупой угол и обтекаемый угол. Прямой угол равен 90 градусам и обозначается символом ∟ . Острый угол меньше 90 градусов, а тупой угол больше 90 градусов, но меньше 180 градусов. В центре круга располагается центральный угол, который равен 360 градусам или 2п радиан.
Углы широко применяются в различных областях, включая архитектуру, инженерное дело, физику и географию. Изучение углов позволяет нам определить геометрические свойства объектов, рассчитывать расстояния и углы, а также разрабатывать строительные проекты и прогнозировать результаты физических экспериментов.
Определение и основные понятия
Центральным углом называется угол, вершина которого совпадает с центром окружности, а стороны проходят через точки на окружности. Он обозначается греческой буквой Θ (альфа-угол).
Центральный угол является частным случаем направленного угла, у которого обе стороны проходят через окружность. Он определяет дугу окружности, которую он охватывает.
Угол, отличный от 360°, называется неполным центральным углом. Полный центральный угол равен 360° и охватывает всю окружность.
Центральные углы используются в геометрии и математике для решения задач, связанных с окружностями и дугами. Они имеют важное значение при изучении геометрии окружности, круга и углов, а также при решении задач по тригонометрии и геометрии в пространстве.
Виды углов и их классификация
1. По величине
Углы делятся на три категории в зависимости от их величины:
- Острый угол: угол, значение которого меньше 90 градусов.
- Прямой угол: угол, значение которого равно 90 градусов.
- Тупой угол: угол, значение которого больше 90 градусов, но меньше 180 градусов.
2. По положению сторон
Углы также могут быть классифицированы в зависимости от положения их сторон:
- Смежные углы: углы, имеющие общую сторону и одну точку пересечения.
- Вертикальные углы: углы, находящиеся на противоположных сторонах пересекающихся прямых и равные между собой.
- Дополнительные углы: пара углов, сумма которых равна 180 градусов.
- Суплементарные углы: пара углов, сумма которых равна 90 градусов.
Знание различных видов углов и их классификации поможет лучше понять геометрические свойства и использовать их в практических задачах.
Особые углы в геометрии
В геометрии существуют различные особые углы, которые имеют свои важные свойства и назначения.
Центральный угол
Центральный угол — это угол, вершина которого находится в центре окружности. Он может быть конечным или полным, в зависимости от длины дуги, которую он охватывает.
Центральные углы имеют ряд особенностей. Например, центральный угол совпадает с углом, образованным диаметром и касательной, проведенными к одной и той же точке на окружности.
Свойства центрального угла:
- Его мера выражается числом градусов, которые он охватывает.
- Он равен половине меры дуги, которую он охватывает.
- Его дополнительный угол тоже является центральным и имеет равную меру.
Центральные углы играют важную роль в геометрии, особенно при решении задач, связанных с окружностями и дугами. Изучение их свойств поможет понять и применять геометрические концепции в практических задачах.
Центральные углы
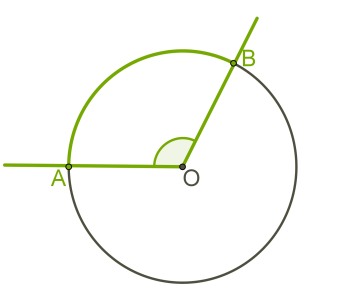
Центральным углом называется угол, вершина которого лежит в центре окружности. Центральный угол измеряется между двумя лучами, и эти лучи соединяют вершину угла с точками на окружности. Луч, исходящий из центра и проходящий через вершину, называется радиусом. Другие лучи, соединяющие вершину с точками на окружности, называются сторонами центрального угла.
Центральные углы используются в геометрии для описания положения и свойств фигур на плоскости. Они также имеют важное значение в круговой геометрии, так как они позволяют определить положение точек на окружности и внутри нее. Центральные углы могут быть разного размера — от 0 до 360 градусов.
Основные свойства центральных углов:
- Сумма центральных углов, заключенных в одной окружности, всегда равна 360 градусов. Это свойство можно использовать для решения задач, связанных с определением измерения центрального угла или нахождением неизвестного угла по данным.
- Центральный угол, равный 180 градусов, называется прямым углом. Он делит окружность на две равные части и соответствует делению окружности на половину — полукруг.
- Если центральный угол меньше 180 градусов, то он называется остроугольным углом. В этом случае, его стороны находятся внутри окружности.
- Если центральный угол больше 180 градусов, то он называется тупоугольным углом. В этом случае, его стороны находятся вне окружности.
- Центральный угол в размере 360 градусов называется полным углом. Он охватывает все точки на окружности и соответствует делению окружности на целое.
Центральные углы имеют множество приложений в геометрии и физике. Они используются для определения дуговых отрезков, нахождения площади секторов окружности, а также для описания движения объектов по окружности, например, при изучении движения планет или электронов в атоме.
Свойства и примеры центральных углов
Свойства центральных углов:
| Свойство | Описание |
|---|---|
| Величина угла | Центральный угол равен вдвое углу, образованному соответствующей дугой окружности. |
| Он соответствует дуге | Центральный угол и дуга окружности, на которой он расположен, имеют одну и ту же меру. |
| Углы на разных окружностях | Если две окружности пересекаются или касаются, центральные углы на них, образованные одной и той же дугой, равны. |
Примеры центральных углов включают углы, образованные дугой окружности:
- Угол в центре окружности.
- Угол, образованный хордой и радиусом, исходящим из центра окружности.
- Угол, образованный диаметром и хордой, проходящей через его конец.
Центральные углы являются важными концепциями в геометрии и применяются в различных областях, включая строительство, дизайн и научные исследования.
Как измерить центральный угол
Чтобы измерить центральный угол, необходимо выполнить следующие шаги:
Шаг 1: Закрепите центральную точку
Возьмите компас и поставьте его ножку в центр окружности. Эта точка будет служить вершиной угла.
Шаг 2: Расположите точку на окружности
С помощью другой ножки компаса выберите точку на окружности, через которую будет проходить одна из сторон угла. Расставьте точки на других сторонах угла таким же образом.
Обратите внимание, что все три точки должны быть размещены на окружности.
Шаг 3: Измерьте угол с помощью угломера или транспортира.
Поместите угломер/транспортир на вершину угла (центральную точку). Одна из сторон угла должна совпадать с базовой линией угломера/транспортира. Затем прочтите значение угла на устройстве.
Шаг 4: Запишите измерение угла.
Полученный результат можно записать в градусах или радианах, в зависимости от использованного устройства измерения.
Если у вас нет угломера или транспортира, можно использовать следующий метод:
Альтернативный способ: Используйте тикающие часы
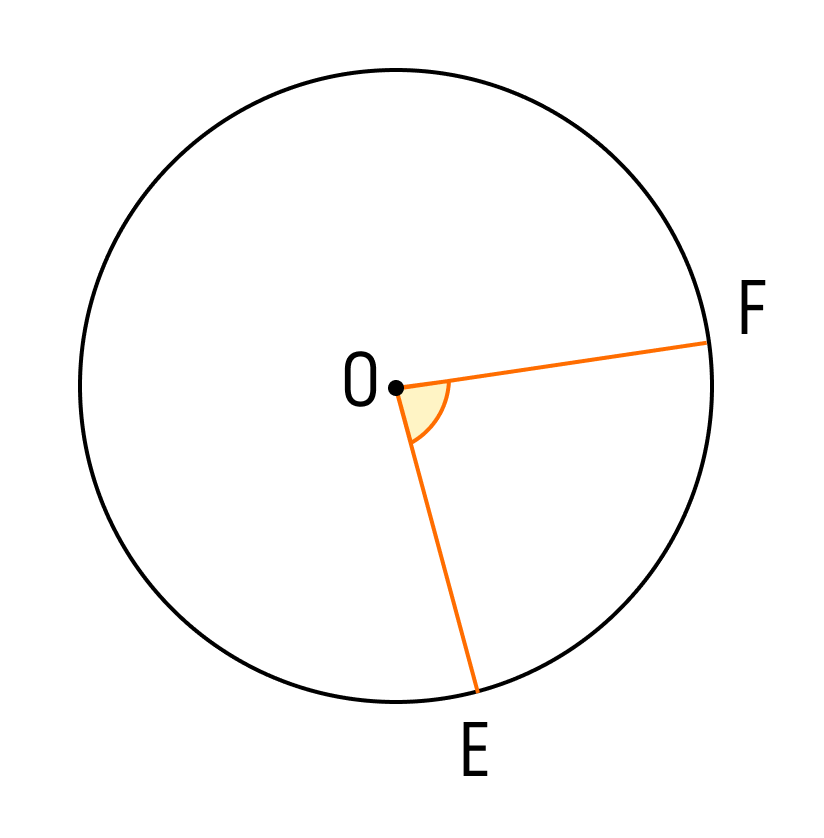
Разместите центр окружности в центре часового циферблата и прочитайте значение между вершиной угла и другой стороной.
Данный метод не является точным, но может использоваться в ситуациях, когда нет доступа к угломеру или транспортиру.
Интересно отметить, что для измерения центрального угла необходимо знать радиус окружности и две точки на ее ободе.
Теперь, когда вы знаете, как измерить центральный угол, вы можете применить этот метод для решения различных задач, связанных с углами в геометрии и физике.
Применение центральных углов
Геодезия и навигация
Центральные углы используются в геодезии и навигации для определения направления и расстояния между точками на Земле. Геодезические измерения на основе центральных углов позволяют строить карты, определять границы земельных участков и проводить навигацию по местности.
Телекоммуникации
В области телекоммуникаций центральные углы используются для определения направления передачи сигнала. Например, антенны радио и телевизионных станций нацелены на центральные углы, что обеспечивает наилучшую передачу сигнала в данном направлении.
Важно отметить, что центральные углы играют большую роль в оптике, астрономии, графике и других науках и технических областях, где изучается форма и геометрия объектов.
Использование центральных углов помогает упростить анализ и решение задач, связанных с геометрией и пространственными отношениями. Благодаря своей простоте и удобству применения, центральные углы стали неотъемлемым инструментом в работе геометров, инженеров, архитекторов и других специалистов, работающих с фигурами и объектами на плоскости и в пространстве.
Вопрос-ответ:
Что представляет собой центральный угол?
Центральный угол — это угол, вершина которого находится в центре окружности, а стороны проходят через точки окружности.
Каково свойство центральных углов?
Свойство центральных углов состоит в том, что их меры равны, если они опираются на одну и ту же дугу окружности.
Чем отличается центральный угол от других типов углов?
Центральный угол отличается тем, что его вершина находится в центре окружности, в то время как у других углов вершина может находиться в любой точке пространства.
Когда стоит использовать понятие центрального угла в геометрии?
Понятие центрального угла широко используется в геометрии для изучения свойств окружностей и дуг. Центральные углы помогают определить взаимное расположение точек на окружности и находить равные углы.