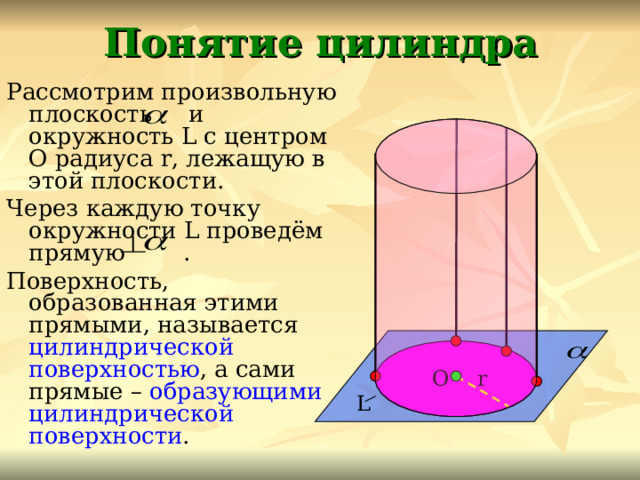
Цилиндр – геометрическое тело, которое всегда привлекало внимание и вызывало интерес у ученых и математиков. Оно представляет собой особую форму геометрического тела, ограниченного двумя параллельными плоскостями — верхней и нижней основами, а также боковой поверхностью в виде кругового цилиндра.
Хотя цилиндром называется множество предметов в повседневной жизни (чашки, стаканы, банки), в математике его определение сложнее и подразумевает абстрактное представление. Для математиков цилиндр – это некий геометрический объект, который обладает рядом уникальных свойств и характеристик.
Важно понимать, что геометрическое свойство цилиндра состоит в том, что его боковая поверхность представляет собой плоскость-секущую, спараллельную основам, в результате чего она оказывается в форме круга. Эта форма является общественным признаком большинства цилиндров в нашей реальности.
Определение и основные характеристики цилиндра
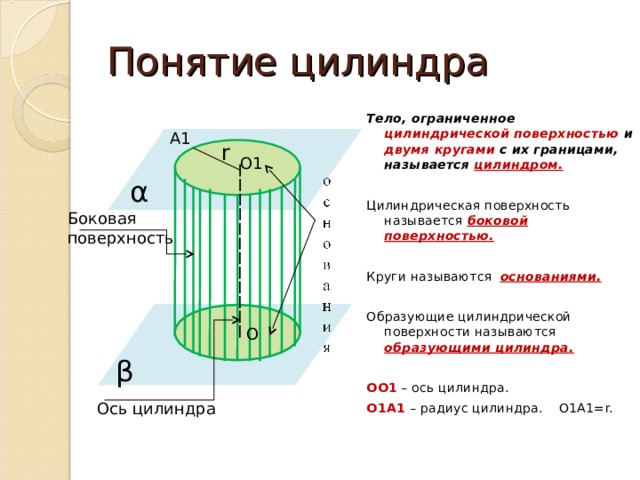
Цилиндром называется тело, ограниченное поверхностью, состоящей из двух плоских оснований, которые параллельны и идентичны друг другу, а также из боковой поверхности, которая представляет собой кривую, образующую замкнутую фигуру.
Основные характеристики цилиндра:
- Высота цилиндра — это расстояние между плоскими основаниями. Она может быть любой положительной величиной.
- Радиус цилиндра — это расстояние от центра одного из оснований до точки на боковой поверхности. Радиус является неотрицательной величиной.
- Объем цилиндра — это количество пространства, занимаемого цилиндром. Объем цилиндра можно вычислить по формуле: V = π * r² * h, где V — объем, π — постоянное число, равное примерно 3,14 (или можно использовать значение π из модуля math в программировании), r — радиус основания, h — высота цилиндра.
- Площадь боковой поверхности цилиндра — это сумма площадей всех боковых поверхностей цилиндра. Площадь боковой поверхности можно вычислить по формуле: Sб = 2π * r * h, где Sб — площадь боковой поверхности, π — постоянное число, равное примерно 3,14 (или можно использовать значение π из модуля math в программировании), r — радиус основания, h — высота цилиндра.
- Полная поверхность цилиндра — это сумма площадей всех его поверхностей, включая основания и боковую поверхность. Полную поверхность цилиндра можно вычислить по формуле: Sп = 2π * r * (r + h), где Sп — полная поверхность, π — постоянное число, равное примерно 3,14 (или можно использовать значение π из модуля math в программировании), r — радиус основания, h — высота цилиндра.
Цилиндры встречаются в различных областях науки и техники, их свойства широко применяются в геометрии, физике, инженерии и многих других областях.
Структура и форма цилиндра
Цилиндром называется тело ограниченное поверхностью, которая представляет собой две параллельные плоскости (основания цилиндра), соединенных криволинейной поверхностью (боковой поверхностью).
Основания цилиндра имеют форму кругов, вокруг которых описывается боковая поверхность. Круговая форма оснований делает цилиндр симметричным относительно оси, проходящей через центры оснований.
Боковая поверхность цилиндра состоит из всех точек, лежащих на прямых, параллельных оси цилиндра. В случае круглого цилиндра, боковая поверхность представляет собой цилиндрическую поверхность.
Размеры цилиндра
Цилиндр характеризуется несколькими размерами:
- Радиус основания — это расстояние между центром основания и точкой на окружности основания.
- Высота цилиндра — это перпендикулярное расстояние между плоскостью основания и плоскостью, параллельной основанию и проходящей через вершину цилиндра.
- Объем цилиндра — это количество пространства, которое ограничивается его поверхностью.
Применение цилиндра
Цилиндры широко применяются во многих областях науки, техники и повседневной жизни. Их форма и структура делают их удобными для хранения и транспортировки жидкостей и газов. Также цилиндры используются в двигателях, насосах, гидравлических системах, технических приспособлениях и других устройствах.
Различные виды цилиндров
В мире существует множество различных типов цилиндров, которые могут использоваться в различных сферах деятельности. Ниже перечислены некоторые из них:
Цилиндр с плоским дном и крышкой
Самый распространенный тип цилиндра, который мы используем практически каждый день, — это цилиндр с плоским дном и крышкой. У него есть два основания — одно в форме круга, называемое «дном», и другое также в форме круга, называемое «крышкой». Основания связаны параллельными сторонами — боковой образующей, которая является прямой линией.
Цилиндр с наклонным дном и плоской крышкой
Этот тип цилиндра имеет основание, которое наклонено по отношению к направлению боковой образующей. Оно может быть в форме эллипса или другой необычной формы. Крышка у этого цилиндра всегда плоская и параллельна дну. Такие цилиндры часто используются в научных исследованиях или при производстве специального оборудования.
Это лишь некоторые из многих видов цилиндров, которые можно встретить в жизни. Каждый из них имеет свои особенности и применения в различных областях науки, техники и промышленности.
Преимущества использования цилиндров
Цилиндром называется тело, ограниченное поверхностью, состоящей из двух параллельных и равных окружностей вместе с заключенной между ними боковой поверхностью. Из-за своей геометрической формы, цилиндры обладают рядом преимуществ:
1. Высокая механическая прочность. Благодаря своей форме и структуре, цилиндры способны выдерживать большие механические нагрузки, что делает их идеальным инструментом для использования в промышленности и строительстве.
2. Простота в использовании и монтаже. Цилиндры легко монтируются и устанавливаются в различных системах и оборудовании. Эта простота в использовании позволяет сократить время и упростить процесс монтажа в промышленных и строительных проектах.
3. Большой объем хранения. Благодаря своей форме и структуре, цилиндры имеют большой объем внутреннего пространства для хранения жидкостей и газов. Это особенно важно в промышленности, где требуется хранение больших объемов различных веществ.
4. Устойчивость к давлению. Цилиндры обладают хорошей устойчивостью к давлению, что позволяет использовать их в системах, требующих передачи жидкостей и газов под давлением.
5. Возможность сочетания с другими формами. Цилиндры легко сочетаются с другими геометрическими формами, что позволяет создавать сложные системы и устройства для различных целей.
Благодаря своим преимуществам, цилиндры широко используются в различных сферах промышленности, строительства и техники.
Применение цилиндров в различных отраслях
Автомобильная промышленность
Цилиндры широко применяются в автомобильной промышленности. Они используются, например, в двигателях внутреннего сгорания. В таких двигателях цилиндры служат для сжатия и сгорания топлива, а также для передачи энергии от горения к поршню. Более современные автомобилей могут также использовать цилиндрические батареи для хранения энергии или газовые цилиндры для сжатого природного газа как альтернативного источника топлива.
Медицинская отрасль
Цилиндры также находят широкое применение в медицинской отрасли. Например, для хранения и транспортировки газов медицинского назначения, таких как кислород. Цилиндрические емкости с кислородом используются в больницах и скорых помощниках, чтобы предоставить пациентам необходимое количество кислорода для дыхания.
| Отрасль | Применение |
|---|---|
| Строительство | Использование цилиндров для создания столбов фундаментов |
| Нефтегазовая промышленность | Хранение и транспортировка газов с помощью цилиндров |
| Производство | Использование цилиндров в прессовании и формовке материалов |
Все эти примеры демонстрируют широкое применение цилиндров в различных отраслях, где они играют важную роль в хранении, передаче и использовании газов и других веществ, а также в создании определенных структур и инженерных решений.
Расчеты объема и площади поверхности цилиндра
Объем цилиндра
Объем цилиндра можно рассчитать по формуле: V = Sосн * h, где V — объем цилиндра, Sосн — площадь основания цилиндра, h — высота цилиндра.
Площадь поверхности цилиндра
Площадь поверхности цилиндра складывается из площади двух оснований и площади мантии. Площади оснований можно рассчитать по формуле: Sосн = π * r2, где π — математическая константа, равная примерно 3.14, r — радиус основания цилиндра.
Площадь мантии цилиндра можно рассчитать по формуле: Sмант = 2π * r * h, где h — высота цилиндра.
Итак, площадь поверхности цилиндра равна сумме площади двух оснований и площади мантии: S = 2 * Sосн + Sмант.
Теперь вы знаете, как рассчитать объем и площадь поверхности цилиндра. Эти формулы могут быть полезными при решении различных задач, связанных с цилиндрами.
Свойства и особенности цилиндрических тел

1. Объем цилиндра
Объем цилиндра определяется по формуле V = πr^2h, где π (пи) – математическая константа, равная примерно 3,14; r – радиус основания цилиндра; h – высота цилиндра.
2. Площадь боковой поверхности цилиндра
Площадь боковой поверхности цилиндра вычисляется по формуле Sб = 2πrh, где π (пи) – математическая константа, равная примерно 3,14; r – радиус основания цилиндра; h – высота цилиндра.
Кроме того, цилиндры обладают рядом других свойств и особенностей. Они могут быть прямыми или наклонными, в зависимости от положения оси цилиндра. Цилиндры широко применяются в различных сферах, таких как инженерное дело, строительство, техника и даже в кулинарии.
| Название свойства | Описание |
|---|---|
| Диаметр цилиндра | Диаметр цилиндра – это двукратное расстояние между точками на окружности основания цилиндра |
| Объем цилиндра | Объем цилиндра определяется по формуле V = πr^2h, где π (пи) – математическая константа, равная примерно 3,14; r – радиус основания цилиндра; h – высота цилиндра. |
| Площадь боковой поверхности цилинда | Площадь боковой поверхности цилиндра вычисляется по формуле Sб = 2πrh, где π (пи) – математическая константа, равная примерно 3,14; r – радиус основания цилиндра; h – высота цилиндра. |
Итак, цилиндры – это особые фигуры, которые имеют свои уникальные свойства и широко применяются в различных областях науки и техники.
Примеры реальных объектов, имеющих форму цилиндра
1. Банка из-под газировки
Одним из самых распространенных примеров цилиндра является банка из-под газировки. Она имеет цилиндрическую форму с плоским дном и крышкой. Благодаря своей форме, банка удобно укладывается в холодильник или сумку.
2. Аккумулятор для автомобиля
Еще одним примером объекта, имеющего форму цилиндра, является аккумулятор для автомобиля. Он также имеет цилиндрическую форму, что позволяет его легко размещать в моторном отсеке автомобиля.
На самом деле, примеров объектов с формой цилиндра гораздо больше. В таблице ниже приведены еще некоторые из них.
| Объект | Описание |
|---|---|
| Сосуды для кипячения воды (чайники) | Чирейки, кофеварки, электрочайники — все они имеют форму цилиндра, позволяющую равномерно нагревать воду. |
| Бутылки с водой | Бутылки с водой, газировкой и другими напитками часто имеют цилиндрическую форму, облегчающую их транспортировку и хранение. |
| Трубы | Трубы, используемые в строительстве и водоснабжении, имеют форму цилиндра, позволяющую обеспечить прочность и устойчивость конструкции. |
Таким образом, цилиндрическая форма широко используется в различных областях нашей жизни и присутствует во множестве реальных объектов.
Вопрос-ответ:
Что такое цилиндр?
Цилиндром называется тело ограниченное поверхностью, образующейся при движении параллельных прямых линий при их постоянном удалении друг от друга.
Какие основные свойства цилиндра?
Основные свойства цилиндра: он имеет две параллельные плоскости (основания), соединенные боковой поверхностью; все боковые грани его параллельны основаниям; все боковые грани цилиндра имеют одинаковую форму и равны между собой.
Как найти объем цилиндра?
Объем цилиндра можно найти по формуле: V = П * r^2 * h, где V — объем, П — число Пи (3,14), r — радиус основания цилиндра, h — высота цилиндра.
Чем отличается прямой цилиндр от наклонного?
Прямой цилиндр — это тот, у которого оси его оснований перпендикулярны плоскости основания, а наклонный цилиндр — это тот, у которого оси его оснований наклонены относительно плоскости основания.
Где в жизни встречаются цилиндры?
Цилиндры встречаются во многих сферах жизни, например: банки от консервов, стаканы, трубы, столбы и колонны, вазы, множество предметов мебели и многое другое.
Как определить объем цилиндра?
Объем цилиндра можно определить по формуле: V = П * r^2 * h, где П — число «пи» (около 3,14), r — радиус основания цилиндра, h — высота цилиндра.