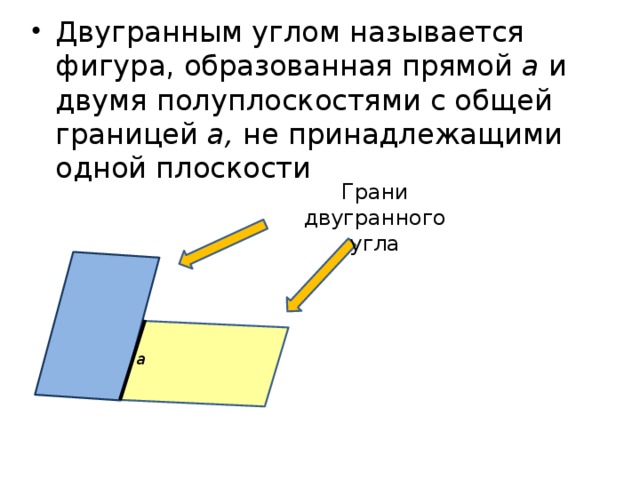
Двугранным углом называется фигура, которая образуется двумя лучами, исходящими из одной точки. Он получил такое название благодаря своей форме, которая напоминает две грани прямого угла. Двугранный угол является одной из основных фигур в геометрии и имеет свои уникальные свойства и конструкцию.
Конструкция двугранного угла осуществляется путем проведения двух лучей из одной точки. Эти лучи называются сторонами угла, а их общая начальная точка называется вершиной угла. Для обозначения двугранного угла используется специальная нотация: отрезком, соединяющим вершину угла с серединой одной из его сторон. Например, если одна из сторон угла AB, то двугранный угол обозначается как ∠BAC или ∠CAB.
Основные свойства двугранного угла включают его измерение и сумму двугранных углов. Измерение двугранного угла происходит в градусах или радианах и зависит от величины открытой части угла. Сумма двугранных углов равна 180 градусам или пи радианам, так как они образуют линию, которая противоположна прямому углу.
Двугранный угол — это одна из фундаментальных фигур в геометрии, существующая с древних времен. Он широко используется в различных областях, таких как архитектура, инженерия, физика и другие. Изучение свойств двугранного угла помогает углубить понимание геометрии и применять его в практических задачах.
Определение двугранного угла
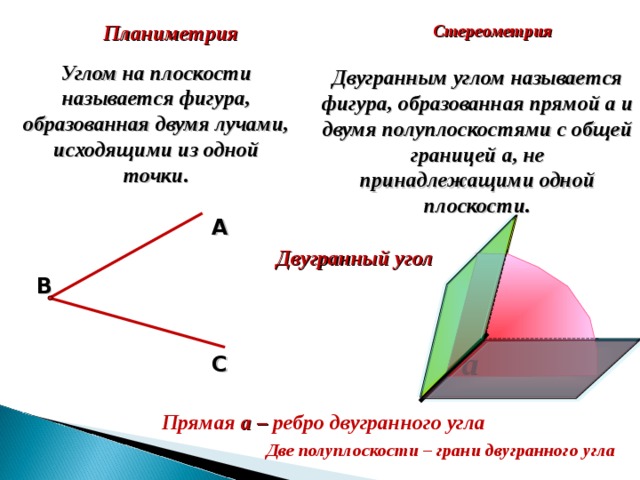
Двугранным углом называется фигура, образованная двумя сторонами, их общей вершиной, и лежащая в одной плоскости. Двугранные углы также называются углами второго порядка.
Двугранный угол состоит из двух полупрямых лучей, называемых сторонами угла, и общей начальной точкой, называемой вершиной угла. Стороны угла лежат в одной плоскости и располагаются относительно друг друга под определенным углом. Угол измеряется в градусах или радианах, в зависимости от системы измерения углов.
Двугранные углы можно классифицировать по их величине. Малые углы имеют меру меньше 90 градусов или меньше $\frac{\pi}{2}$ радианов, что соответствует острому углу. Прямой угол имеет меру 90 градусов или $\frac{\pi}{2}$ радианов. Большие углы имеют меру больше 90 градусов или больше $\frac{\pi}{2}$ радианов, что соответствует тупому углу.
Примеры двугранных углов:
1. Острый угол: угол, мера которого меньше 90 градусов. Например, угол между сторонами треугольника.
2. Прямой угол: угол, мера которого равна 90 градусам или $\frac{\pi}{2}$ радианам. Например, угол между пересекающимися прямыми.
3. Тупой угол: угол, мера которого больше 90 градусов. Например, угол между пересекающимися полупрямыми.
Важно отметить, что двугранные углы могут суммироваться или вычитаться в зависимости от своей величины и направления.
Таким образом, двугранный угол — это геометрическая фигура, состоящая из двух сторон, общей вершины и лежащая в одной плоскости.
Грани и вершины двугранного угла
Двугранным углом называется фигура, образованная двумя лучами, имеющими одну общую точку, которая называется вершиной. Пространство между этими лучами называется плоскостью, которая разделяет угол на две части.
Для двугранного угла характерны две грани. Каждая грань является плоскостью, прилегающей к сторонам угла. Грани являются непрерывными поверхностями и образуют ребра, которые являются линиями пересечения двух граней.
У двугранного угла также есть вершины. Вершины двугранного угла представляют собой точки пересечения ребер и граней. Вершины могут быть одна или несколько в зависимости от формы и размеров угла. Обычно указывается число вершин, например, трехгранный угол имеет три вершины.
Каждая грань двугранного угла имеет свою форму и может быть плоскостью любой сложности. Грани могут быть плоскими, кривыми или иметь сложную полигональную форму. Количество граней и их форма определяют конкретный вид двугранного угла.
Грани и вершины двугранного угла играют важную роль в геометрии и применяются для решения различных задач и конструкций. Понимание граней и вершин помогает увидеть связь между различными углами и рассчитать их характеристики, такие как площадь или объем.
Свойства двугранного угла
Свойство 1: Сумма мер двугранных углов
Сумма мер двугранных углов равна 360 градусов.
Свойство 2: Отношение мер двугранных углов
Отношение мер двугранных углов можно выразить в виде дроби, где числитель — мера одного угла, а знаменатель — мера другого угла.
Например, если один угол имеет меру 120 градусов, а другой — 240 градусов, то отношение мер этих углов будет 1:2.
Свойство 3: Дополняющие двугранные углы
Дополняющие двугранные углы — это два угла, сумма мер которых равна 180 градусов.
Свойство 4: Смежные двугранные углы
Смежные двугранные углы — это два угла, общая вершина которых лежит на одном луче, а стороны этих углов противоположны друг другу.
Например, если одна из вершин двугранного угла A лежит на конце стороны другого угла B, то эти углы будут смежными.
У двугранного угла есть еще ряд свойств, которые могут быть использованы для решения геометрических задач. Ознакомившись с этими свойствами, вы сможете легче работать с двугранными углами и использовать их в своих расчетах и измерениях.
Виды двугранных углов
Двугранным углом называется фигура, образованная двумя лучами с общим началом. В зависимости от размеров углов и их соотношений существуют различные виды двугранных углов. Рассмотрим некоторые из них:
Острый угол: острый угол имеет размер менее 90 градусов. По своей форме он напоминает букву «V». Острый угол можно наблюдать, например, при сгибании листа бумаги.
Прямой угол: прямой угол имеет размер 90 градусов. Он выглядит как угол, составленный прямо вертикально. Примером такого угла может служить угол, сформированный стенами в комнате.
Тупой угол: тупой угол имеет размер больше 90 градусов, но меньше 180 градусов. Такой угол имеет форму, похожую на букву «L» или открытую дверь.
Разносторонний угол: разносторонний угол — это угол, у которого все стороны имеют разную длину. Такой угол может быть как остроугольным, так и тупоугольным.
Равнобедренный угол: равнобедренный угол имеет две равные стороны и две равные вершины. Такой угол может быть как остроугольным, так и тупоугольным. Примером равнобедренного угла может служить угол внутри равнобедренного треугольника.
Полный угол: полный угол имеет размер 180 градусов и является самым большим из двугранных углов. Он представляет собой прямую линию, разделенную на две равные части.
Изучение и классификация двугранных углов позволяет нам лучше понимать их свойства и применять эту информацию в геометрии и других науках.
Измерение углов в плоском двугранном углу
Для измерения углов в плоском двугранном углу используются различные инструменты и методы. Они позволяют определить величину углов и провести различные геометрические построения.
Инструменты для измерения углов:
1. Угломер – специальный инструмент, состоящий из двух неподвижных линеек, с помощью которого можно измерять углы.
2. Гониометр – прибор для измерения углов, использующийся в геодезии и астрономии.
Методы измерения углов:
1. Визуальный метод – самый простой, но не всегда точный способ. В этом случае измерение основано на визуальном определении угла с помощью угломера или гониометра.
2. Графический метод – основан на построении графических прямых и определении углов по ним. Этот метод используется, например, при построении треугольников.
3. Тригонометрический метод – использует тригонометрические соотношения для определения размеров углов.
Измерение углов в плоском двугранном углу – важный элемент геометрии и науки о строении фигур. Корректное измерение углов позволяет проводить точные геометрические построения и решать различные задачи.
Формулы для вычисления площади двугранного угла
Двугранным углом называется фигура, образованная двумя плоскостями, которые пересекаются по общей прямой. Площадь двугранного угла можно вычислить с помощью нескольких формул.
Формула с использованием углового коэффициента
Для вычисления площади двугранного угла можно использовать следующую формулу:
S = α * l^2,
где S — площадь двугранного угла, α — угловой коэффициент, l — длина общей прямой, по которой пересекаются плоскости.
Формула с использованием углового диаметра
Еще одной формулой для вычисления площади двугранного угла является:
S = π * d^2 * (1 — |cos(α)|),
где S — площадь двугранного угла, π — число Пи (приближенное значение 3,14159), d — диаметр общей прямой, по которой пересекаются плоскости, α — угол между плоскостями.
Отметим, что для вычисления площади двугранного угла необходимо знать длину общей прямой или диаметр общей прямой, а также угловой коэффициент или угол между плоскостями.
Эти формулы являются основными для вычисления площади двугранного угла и могут быть использованы в различных математических и геометрических расчетах.
Примеры использования двугранных углов
Двугранные углы широко применяются в геометрии и инженерии. Они играют важную роль в решении различных задач, включая построение и измерение углов, а также в архитектуре и дизайне.
Архитектура
В архитектуре двугранные углы используются для создания эффектов перспективы и добавления глубины в дизайн зданий. Например, двугранный угол может быть использован для создания зрительной иллюзии, что здание выглядит более высоким или широким, чем на самом деле. Этот прием часто используется в современной архитектуре, чтобы добавить динамизма и уникальности внешнему виду здания.
Инженерия
В инженерии двугранные углы широко применяются в построении, измерении и решении различных задач. Например, в градостроительстве инженеры используют двугранные углы для определения направления движения дорог, создания эффективных плоскостей при построении зданий, а также для ориентации объектов на местности.
- В авиации и морской навигации двугранные углы используются для определения направления движения и для навигации в пространстве.
- В машиностроении и проектировании двугранные углы применяются для определения рабочих углов и формы деталей, а также для расчета сопротивления материалов.
Это лишь некоторые примеры использования двугранных углов. Они играют важную роль во многих областях науки и техники, и их правильное использование является ключевым элементом в решении многих задач.
Вопрос-ответ:
Как определить двугранный угол?
Двугранный угол — это фигура, образованная двумя лучами, которые исходят из одной точки. Чтобы определить двугранный угол, нужно провести эти лучи и посмотреть, есть ли у них общая вершина.
Какие свойства имеет двугранный угол?
Двугранный угол обладает несколькими свойствами. Во-первых, сумма его двух углов равна 180 градусам. Во-вторых, двугранный угол можно расширить или уменьшить, сохраняя его форму. В-третьих, двугранные углы могут быть прилегающими, если у них общая сторона.
Где в жизни можно встретить двугранный угол?
Двугранные углы можно встретить в различных ситуациях в жизни. Например, они часто встречаются в геометрии, в архитектуре, в дизайне, в строительстве и в других областях, где используются углы и прямые линии.
Может ли двугранный угол быть равным 90 градусов?
Нет, двугранный угол не может быть равным 90 градусам. Поскольку сумма углов двугранного угла равна 180 градусам, оба угла этой фигуры должны быть меньше или больше 90 градусов.
Как использовать двугранный угол в реальной жизни?
Двугранные углы можно использовать в различных сферах жизни. Например, они могут быть использованы в архитектуре для создания интересных форм зданий, в дизайне для создания эффекта перспективы, или в геометрии для решения задач по нахождению неизвестных углов.
Что такое двугранный угол?
Двугранным углом называется фигура, образованная двумя полупрямыми, исходящими из общей точки. Угол внутри фигуры называется внутренним углом, а угол вне фигуры называется внешним углом. Двугранный угол может быть остроугольным, тупоугольным или прямым.