Определение и функции биссектрисы треугольника

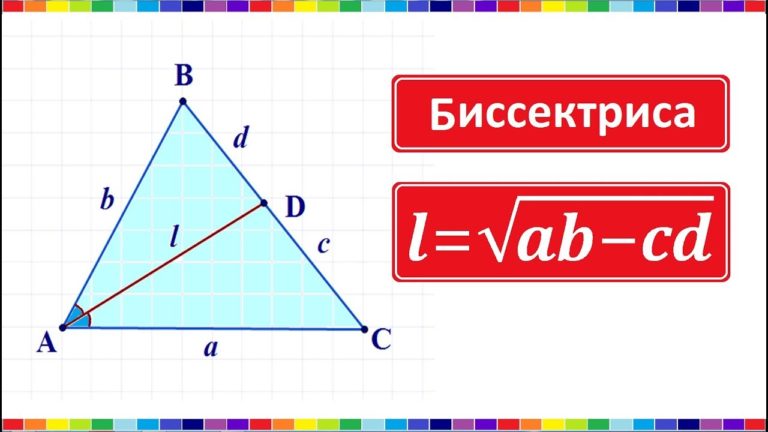
Биссектрисой треугольника называют прямую, которая делит угол на две равные части. Конечные точки биссектрисы лежат на сторонах угла, а сама биссектриса проходит через вершину угла. Биссектриса может быть внутренней или внешней по отношению к треугольнику, в зависимости от того, где она расположена относительно треугольника.

Внутренняя биссектриса делит треугольник на два треугольника, которые имеют равные площади. Она также является перпендикуляром к стороне треугольника и проходит через точку пересечения высот треугольника.

Внешняя биссектриса делит внешний угол треугольника на две равные части. Она также пересекает продолжения сторон треугольника и создает новые треугольники. Внешняя биссектриса является продолжением внутренней биссектрисы до пересечения с продолжением стороны треугольника.

Различные свойства биссектрис треугольника могут быть использованы для решения задач, связанных с треугольниками. Нахождение биссектрисы треугольника может быть полезным для определения точки вписанной окружности треугольника, или для нахождения точки пересечения биссектрис треугольника.

Что такое биссектриса треугольника?

Каждый треугольник имеет три биссектрисы — одну для каждого из своих углов. Биссектрисы пересекаются в одной точке, которая называется центром вписанной окружности треугольника.

Свойства биссектрис треугольника:

• Биссектриса треугольника делит сторону, противолежащую данному углу, на отрезки в пропорции длин двух других сторон треугольника.
• Одна из двух биссектрис каждого угла треугольника является внутриугольной, а другая — внешниугольной.
• Биссектриса внутри треугольника всегда лежит внутри треугольника, а биссектриса внешняя — за его пределами.
• Сумма длин двух внутриугольных биссектрис треугольника всегда больше длины третьей биссектрисы.

Биссектрисы важны при решении различных задач и свойств треугольников. Они применяются в геометрии и помогают определить такие величины, как площадь треугольника, высоты, длины сторон и других линейных отрезков.

Определение и основные понятия:

В геометрии биссектрисой треугольника называют прямую линию, которая делит угол треугольника на два равных по величине угла. Биссектриса обозначается как «б».

Другое определение биссектрисы треугольника: это прямая линия, которая соединяет вершину угла треугольника с серединой противоположной стороны. Таким образом, биссектриса треугольника делит эту сторону на две отрезка, пропорциональных друг другу и соответствующих прилежащим сторонам треугольника.

Основные понятия:

• Вершина угла: точка пересечения двух лучей, образующих угол.
• Середина стороны: точка, которая равноудалена от концов этой стороны.
• Пропорциональные отрезки: отрезки, длины которых обратно пропорциональны.
• Прилежащие стороны: стороны треугольника, которые образуют угол с биссектрисой.

Биссектриса треугольника является важным понятием в геометрии и используется для решения различных задач, например, построения равнобедренного треугольника или нахождения площади треугольника на основе длин его сторон.

Как найти биссектрису треугольника?

Биссектрисой треугольника называется прямая, которая делит один из углов треугольника пополам. Нахождение биссектрисы треугольника позволяет делить его на два равных угла и может быть полезно при решении геометрических задач.

Существует несколько способов найти биссектрису треугольника. Один из них основан на свойствах биссектрисы и треугольника.

1. Выберите любой угол треугольника, который хотите разделить пополам. Обозначим этот угол как В.
2. Продолжите одну из сторон угла В до пересечения с противоположной стороной. Обозначим это точкой А.
3. Проведите биссектрису угла В, которая будет проходить через точку А и делить угол В пополам.

Теперь вы нашли биссектрису треугольника. Это прямая, которая делит угол В пополам и пересекается со стороной угла В в точке А.

Применение биссектрисы треугольника может быть полезно при решении различных задач, например, при построении треугольников по заданным условиям или нахождении площади треугольника с использованием формулы Герона.

Свойства биссектрис треугольника:

Основные свойства биссектрис треугольника:

1. Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные длине смежных сторон.

То есть, если биссектриса пересекает сторону треугольника, то отрезки, на которые она делит эту сторону, будут пропорциональны двум смежным сторонам треугольника. Это свойство называется внутренним делением стороны биссектрисой.

2. Точка пересечения биссектрис треугольника является центром вписанной окружности.

То есть, середина биссектрисы каждого угла треугольника лежит на окружности, которая проходит через точки касания этой биссектрисы со сторонами треугольника. Эта окружность называется вписанной окружностью.

Виды биссектрис треугольника:

1. Внутренняя биссектриса – это линия, которая делит внутренний угол треугольника на две равные части и пересекает противоположную сторону.

2. Внешняя биссектриса – это линия, которая делит внешний угол треугольника на две равные части и пересекает продолжение противоположной стороны.

3. Полувнешняя биссектриса – это линия, которая делит внешний угол треугольника на две равные части и пересекает противоположную сторону.

Знание и понимание этих видов биссектрис треугольника позволяет решать различные задачи, связанные с углами и сторонами треугольника.

Применение биссектрисы треугольника:

1. Геометрия:

   Биссектриса является важным элементом для решения различных задач геометрии. Она позволяет найти точку пересечения биссектрис треугольника, которая является центром вписанной окружности треугольника. Вписанная окружность треугольника имеет значительные геометрические свойства и используется при нахождении других элементов треугольника.

2. Конструктивная геометрия:

   Биссектриса может служить основой для построения других геометрических элементов, таких как медианы треугольника, высоты треугольника, точки ортоцентра и центра окружности, описанной вокруг треугольника.

3. Тригонометрия:

   Биссектриса треугольника позволяет решать задачи с использованием тригонометрических функций. Например, она может использоваться для определения угла треугольника при известных сторонах.

4. Разработка программного обеспечения:

   Биссектриса треугольника может быть использована в алгоритмах, связанных с обработкой геометрических данных или визуализацией треугольников.

Применение биссектрисы треугольника не ограничивается только перечисленными областями, и может находиться в повседневной математике, инженерии, архитектуре и других сферах.

Популярные задачи с использованием биссектрис треугольника:

1. Нахождение точки пересечения биссектрис.

Если в треугольнике провести биссектрисы трех углов, то они пересекутся в одной точке, которая называется центром вписанной окружности. Эта точка имеет множество интересных свойств и используется в решении многих геометрических задач.

2. Нахождение длины биссектрисы.

Длина биссектрисы можно вычислить, используя формулу: l = 2ab/(a+b), где l – длина биссектрисы, a и b – длины отрезков, на которые биссектриса делит противоположные стороны треугольника.

3. Нахождение площади треугольника.

Площадь треугольника можно вычислить, используя формулу: S = (a * b * sin(C))/2, где S – площадь треугольника, a и b – длины сторон треугольника, C – между ними заключенный угол.

4. Нахождение координат точки пересечения биссектрис.

Пересечение биссектрис треугольника определяется как точка, в которой каждая из биссектрис делит отрезок противоположной стороны в отношении длин смежных сторон. Таким образом, можно выразить координаты этой точки, используя известные координаты вершин треугольника.

Интересные факты о биссектрисе треугольника:

1. Суть биссектрисы

   Биссектриса является линией, которая делит внутренний угол на две равные части. Это означает, что каждая биссектриса проходит через середину противолежащей стороны треугольника и делит эту сторону пропорционально к двум другим сторонам.

2. Не всегда проходит через центр вписанной окружности

   Многие люди ошибочно полагают, что биссектриса треугольника проходит через центр вписанной окружности. Однако этот факт справедлив только для равносторонних треугольников. В большинстве других случаев биссектриса не пересекает центр вписанной окружности.

3. Используется для построения медианы

   Биссектриса треугольника играет важную роль в построении медианы – линии, проходящей через вершину треугольника и точку пересечения сторон. Медиана делит сторону треугольника на две равные части и ее длина равна половине длины суммы двух других сторон.

4. Инструмент в геометрических вычислениях

   Биссектрисы треугольника используются в различных геометрических вычислениях, таких как нахождение площади и периметра треугольника, а также построение вспомогательных линий и точек.

Вопрос-ответ:

Что такое биссектриса треугольника?

Биссектриса треугольника — это линия, которая делит угол треугольника на две равные части. Другими словами, биссектриса делит внутренний угол треугольника на два равных угла.

Как найти биссектрису треугольника?

Для того чтобы найти биссектрису треугольника, необходимо провести линию из вершины угла, которую делит этот угол на две равные части. Биссектриса пересекает противоположное ребро треугольника и делит его на две части, пропорциональные сторонам, образующим этот угол.

Зачем нужна биссектриса треугольника?

Биссектриса треугольника является важным элементом для решения различных геометрических задач. Она помогает найти точку пересечения биссектрис треугольника, которая называется центром вписанной окружности. Более того, биссектрисы могут использоваться для нахождения площади треугольника и для доказательства равенства углов.

Как вычислить длину биссектрисы треугольника?

Длина биссектрисы треугольника может быть вычислена с использованием формулы, которая связывает длины сторон треугольника и длину биссектрисы. Формула выглядит следующим образом: длина биссектрисы равна произведению длины одной из сторон треугольника на синус половины внутреннего угла, которым она делится.

Видео:

Биссектриса треугольника.