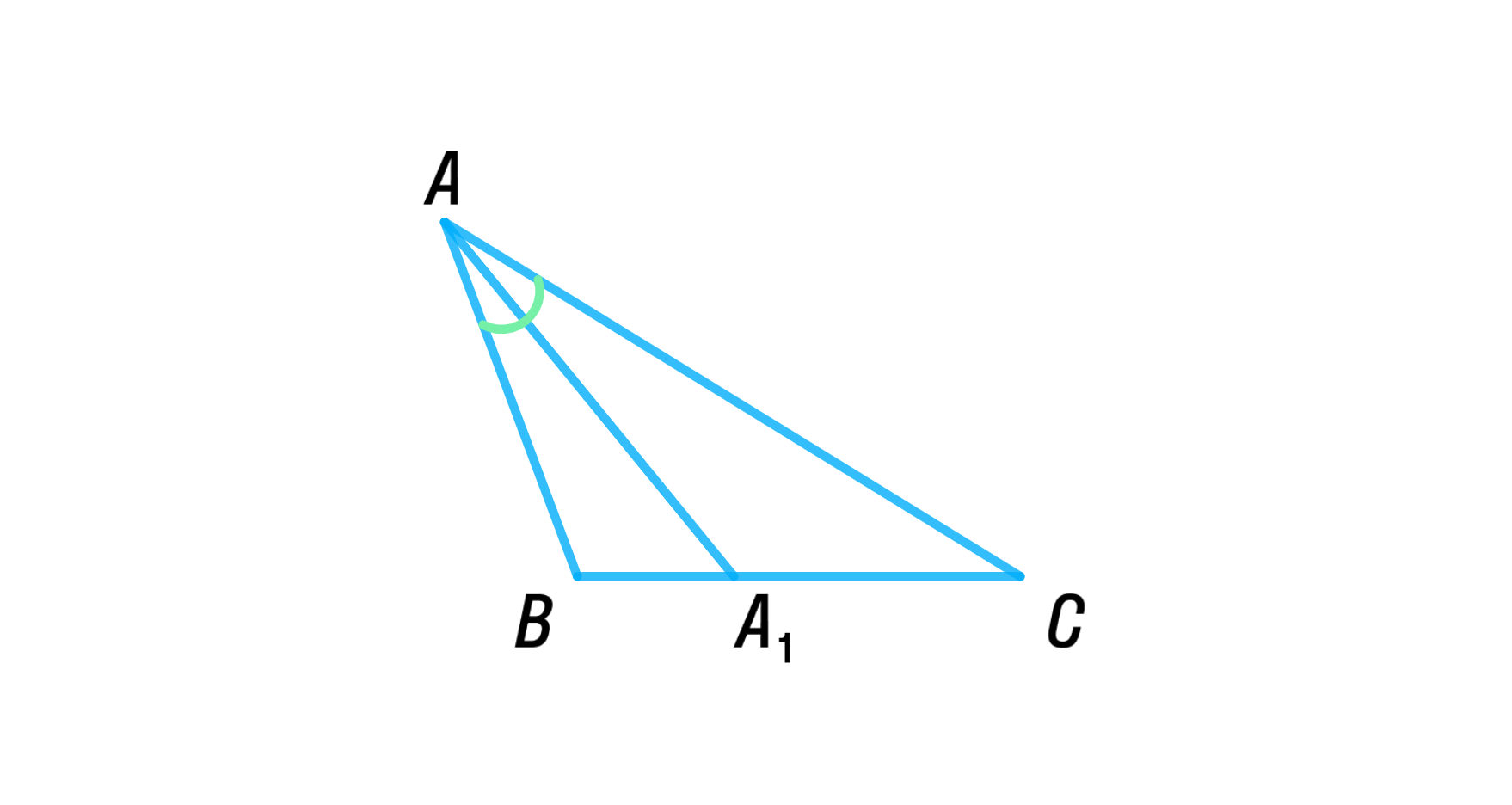
Биссектриса треугольника – это прямая, которая проходит через вершину треугольника и делит противоположный ей угол на два равных угла. Каждый угол треугольника имеет свою биссектрису, и они пересекаются в точке, называемой центром биссектрис. Биссектрисы треугольника играют важную роль в геометрии и могут быть использованы для решения различных задач.
Для каждого из трех углов треугольника существует своя биссектриса. Например, биссектриса угла A – это прямая, которая делит угол A на два равных угла. Биссектриса угла B пересекает сторону AB и сторону BC, а биссектриса угла C пересекает сторону AC и сторону BC.
Важно отметить, что биссектриса треугольника также делит противоположную ей сторону на две отрезка, пропорциональных друг другу. Отношение длин отрезков, на которые биссектриса делит сторону треугольника, определяется теоремой углового биссектриса. Это позволяет использовать биссектрисы для нахождения отношения сторон треугольника и решения геометрических задач на построение.
Определение и свойства
Свойства биссектрис треугольника:
- Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные другим двум сторонам треугольника.
- Точка пересечения биссектрис треугольника, лежащая на противоположной стороне, делит эту сторону на отрезки, пропорциональные другим двум сторонам треугольника.
- Длина биссектрисы треугольника обратно пропорциональна разности длин двух других биссектрис.
- Сумма длин двух биссектрис треугольника всегда больше длины третьей биссектрисы.
Знание определения и свойств биссектрис треугольника важно для понимания и решения разнообразных задач, связанных с треугольниками.
Что представляет собой биссектриса треугольника
Биссектриса является осью симметрии для данного угла и делит его на два равных угла. Таким образом, каждый из полученных углов будет половинным углом исходного угла треугольника.
Треугольник имеет три биссектрисы — одну для каждого из его углов. За счет своей оси симметрии, биссектрисы позволяют найти середину треугольника. Применяя свойства биссектрис треугольника, можно провести параллельные линии и решить различные геометрические задачи.
Вы можете использовать таблицу для отображения свойств биссектрисы треугольника:
| Свойство биссектрисы треугольника | Описание |
|---|---|
| Ось симметрии | Биссектриса является осью симметрии внутреннего угла треугольника и делит его на равные углы. |
| Делит сторону пополам | Биссектриса делит противоположную сторону треугольника на две равные части. |
| Находит середину треугольника | Биссектрисы пересекаются в одной точке, которая является центром окружности, вписанной в треугольник. |
Основные свойства биссектрисы треугольника
Биссектриса имеет несколько важных свойств:
1. Биссектриса треугольника делит противоположную ей сторону на две части пропорционально этим сторонам. То есть, отношение длин отрезков, которые образуются делением стороны биссектрисой, равно отношению других двух сторон треугольника.
2. Точка пересечения биссектрис треугольника с другими биссектрисами и высотами треугольника называется центром вписанной окружности. Она равноудалена от сторон треугольника и является центром окружности, касающейся всех сторон треугольника внутренним образом.
3. Биссектрисы треугольника пересекаются в одной точке, называемой центром вписанной окружности. Эта точка равноудалена от сторон треугольника и делит биссектрисы на отрезки, пропорциональные сторонам треугольника.
Знание и использование основных свойств биссектрисы треугольника помогает решать различные задачи и находить нужные значения в геометрических конструкциях.
Примеры применения биссектрисы треугольника в геометрии
- Нахождение центра вписанной окружности. Пересечение биссектрис трех углов треугольника дает точку, в которой находится центр вписанной окружности. Ее радиус равен расстоянию от центра окружности до любой стороны треугольника.
- Нахождение точки пересечения биссектрис. Пересечение биссектрис двух углов треугольника дает точку, которая является центром окружности, вписанной в угол между этими двумя биссектрисами.
- Нахождение площади треугольника. Биссектриса, проведенная из вершины треугольника к противоположной стороне, делит эту сторону на два отрезка, пропорциональных смежным сторонам. Это свойство биссектрисы позволяет использовать ее для нахождения площади треугольника, поскольку площадь пропорциональна длине этой стороны.
- Нахождение углов треугольника. Биссектрисы углов треугольника могут быть использованы для нахождения значения углов. Зная длины биссектрис и длины сторон треугольника, можно вычислить значения углов с помощью тригонометрических формул.
- Нахождение длины сторон треугольника. Если известна длина биссектрисы и длины других двух сторон треугольника, можно использовать теорему синусов или теорему косинусов для нахождения длины третьей стороны.
Биссектрисы треугольника являются важным инструментом в геометрии и могут быть использованы для решения различных задач, связанных с треугольниками.
Как найти биссектрису треугольника
Чтобы найти биссектрису треугольника, можно использовать следующий алгоритм:
- Выберите одну из вершин треугольника.
- Проведите линию, соединяющую эту вершину с серединой противоположной стороны треугольника.
- Полученная линия и есть искомая биссектриса треугольника.
Таким образом, чтобы найти биссектрису треугольника, необходимо выбрать вершину и провести линию через середину противоположной стороны. Эта линия будет являться биссектрисой угла треугольника.
Зная биссектрису треугольника, можно решать различные задачи, связанные с углами треугольника, например, определение равны ли углы треугольника или какая из сторон треугольника является наибольшей.
Обращаем внимание, что в треугольнике каждый из углов имеет свою биссектрису. Таким образом, в треугольнике всегда существуют три биссектрисы, и они пересекаются в одной точке, которая называется центром вписанной окружности треугольника.
Найти и использовать биссектрисы треугольника может быть полезным при решении геометрических задач или при изучении свойств треугольников в математике.
Метод построения биссектрисы треугольника по описанной окружности
Чтобы построить биссектрису треугольника по описанной окружности, нужно выполнить следующие шаги:
- Нарисуйте треугольник и описанную окружность, отметив все вершины треугольника на окружности.
- Выберите одну из вершин треугольника и проведите хорду через выбранную вершину, соединяющую ее с противоположной вершиной треугольника на описанной окружности.
- Найдите середину проведенной хорды и отметьте эту точку на хорде.
- Проведите прямую через выбранную вершину треугольника и найденную точку на хорде.
- Полученная прямая является биссектрисой треугольника.
Таким образом, построение биссектрисы треугольника по описанной окружности несложно и может быть выполнено с помощью простых геометрических операций.
Метод построения биссектрисы треугольника с использованием углов
Биссектрисой треугольника называется отрезок, который делит внутренний угол треугольника на два равных угла. Этот отрезок соединяет вершину треугольника с соответствующей стороной, расположенной напротив этой вершины.
Метод построения биссектрисы треугольника с использованием углов основан на следующих шагах:
- Выберите вершину треугольника, для которой нужно построить биссектрису.
- Проведите две линии, каждая из которых соединяет данную вершину с вершинами треугольника, образующими угол с этой вершиной. Таким образом, образуются два угла, равные данному углу треугольника.
- Отметьте точку пересечения этих двух линий. Эта точка является вершиной биссектрисы.
- Продолжите проводить линию от выбранной вершины до точки пересечения биссектрисы со стороной треугольника, расположенной напротив этой вершины. Таким образом, получается биссектриса треугольника.
Таким образом, построение биссектрисы треугольника с использованием углов основано на делении угла на два равных угла при помощи проведения линий и нахождении точки пересечения этих линий.
Примеры решения задач по поиску биссектрисы треугольника
Рассмотрим простой пример. Допустим, у нас есть треугольник ABC, где угол ABC равен 60 градусов. Чтобы найти биссектрису угла ABC, мы можем воспользоваться следующей формулой:
Биссектриса = (сторона AB * сторона AC) / (сторона AB + сторона AC)
Для нашего примера, допустим, сторона AB равна 6 и сторона AC равна 8. Подставляем значения в формулу:
Биссектриса = (6 *  / (6 +
/ (6 +  = 48 / 14 ≈ 3.43
= 48 / 14 ≈ 3.43
Таким образом, биссектриса угла ABC примерно равна 3.43.
Другой пример. Теперь предположим, что у нас есть треугольник XYZ, в котором угол XYZ равен 45 градусов, сторона XY равна 5 и сторона XZ равна 7. Применяем формулу:
Биссектриса = (сторона XY * сторона XZ) / (сторона XY + сторона XZ)
Подставляем значения:
Биссектриса = (5 * 7) / (5 + 7) = 35 / 12 ≈ 2.92
Таким образом, биссектриса угла XYZ примерно равна 2.92.
Метод поиска биссектрисы треугольника может варьироваться в зависимости от данной задачи. Однако основная концепция остается неизменной — биссектриса делит угол треугольника пополам. Это позволяет нам легко находить биссектрису, используя соответствующие формулы или геометрические конструкции.
Биссектриса в прямоугольном треугольнике
Биссектрисой треугольника называется отрезок, который делит угол на две равные части. В прямоугольном треугольнике биссектриса имеет особое значение и связана с его высотой и медианами.
Одним из свойств прямоугольного треугольника является то, что биссектриса угла прямоугольного треугольника является его высотой и медианой на гипотенузу. Это означает, что она делит гипотенузу на две части, пропорциональные прилежащим катетам.
Величина биссектрисы в прямоугольном треугольнике рассчитывается по формуле:
биссектриса = (2 * катет1 * катет2)/ (катет1 + катет2)
Найдя значение биссектрисы, можно исследовать связь между биссектрисой, высотой и медианами прямоугольного треугольника. Эти отрезки являются важными элементами для рассмотрения различных свойств и формул, связанных с геометрией треугольника.
Изучение биссектрисы в прямоугольном треугольнике позволяет лучше понять его структуру и взаимосвязи между его элементами.
Примечание: прямоугольный треугольник — это треугольник, у которого один угол равен 90 градусам.
Вопрос-ответ:
Что такое биссектриса треугольника?
Биссектриса треугольника — это прямая, которая делит внутренний угол треугольника на два равных по величине угла.
Какой отрезок называется биссектрисой?
Биссектрисой треугольника называется отрезок, который соединяет вершину треугольника со средней точкой противоположной стороны и делит эту сторону на две равные части.
Как можно найти биссектрису треугольника?
Биссектрису треугольника можно найти, используя формулу для длины биссектрисы: d = 2 * √(abst*(abst — bc)*(abst — ac))/(ab + ac), где a, b и c — длины сторон треугольника, а abst — полупериметр треугольника.
Зачем нужна биссектриса треугольника?
Биссектриса треугольника используется, например, при решении задач на построение треугольника по заданным условиям. Она также может быть полезна при вычислении других характеристик треугольника.
Чем отличается биссектриса треугольника от медианы?
Биссектриса треугольника делит внутренний угол на два равных по величине угла, тогда как медиана делит сторону треугольника на две равные части. Биссектриса и медиана могут иметь разные точки пересечения внутри треугольника.