Какая функция называется монотонной

Монотонная функция – это математическая функция, которая сохраняет порядок значений. Функция называется монотонно возрастающей, если с увеличением значения аргумента ее значение также возрастает или остается постоянным. В свою очередь, функция называется монотонно убывающей, если с увеличением значения аргумента ее значение убывает или остается постоянным.

Монотонные функции имеют большое значение в математике, физике, экономике и других науках. Они позволяют описывать изменение величин и устанавливать связь между различными параметрами. Кроме того, монотонные функции являются основой для изучения более сложных классов функций, таких как вогнутые или выпуклые функции.

Важно отметить, что монотонные функции могут быть определены на отрезке или на всей числовой прямой. Они могут быть заданы как аналитически, так и графически. Определение монотонности функции зависит от набора значений, которые функция принимает на конкретных интервалах аргумента.

Содержание

Что такое монотонная функция и как она определяется?

Монотонная функция может быть строго монотонной или нестрого монотонной. Если значение функции (y) строго возрастает или строго убывает при изменении значения аргумента (x), то функция является строго монотонной.

С другой стороны, если значение функции (y) не увеличивается или не убывает, то функция является нестрого монотонной. Нестрого монотонная функция может быть постоянной — когда значение функции не меняется при изменении аргумента, или монотонной — когда значение функции остается постоянным на каком-то интервале аргумента, но может изменяться на других интервалах.

Для определения монотонности функции сначала необходимо найти производную функции, которая показывает скорость изменения функции при изменении аргумента. Если производная положительна на некотором интервале, то функция строго возрастает на этом интервале. Если производная отрицательна, то функция строго убывает. Если производная равна нулю, то функция может быть постоянной или иметь экстремумы на этом интервале.

Определение монотонности функции:

Найдите производную функции.
Проверьте знак производной на интервалах.
Если производная положительна на интервале, функция строго возрастает на этом интервале.
Если производная отрицательна на интервале, функция строго убывает на этом интервале.
Если производная равна нулю на интервале, функция может быть постоянной или иметь экстремумы на этом интервале.

Знание монотонности функции позволяет анализировать ее свойства и использовать различные методы для решения задач в математике, экономике и других науках.

Монотонность в математике: основные понятия

Монотонность и производная

Монотонная функция – это функция, которая либо всегда возрастает, либо всегда убывает на заданном промежутке. Чтобы проверить монотонность функции, можно использовать производную. Если производная функции всегда положительна на заданном промежутке, то она является строго возрастающей. Если же производная всегда отрицательна, то функция является строго убывающей. Если производная не меняет знак на промежутке, то монотонность может быть невозрастающей или неубывающей.

Монотонность и график функции

Монотонность функции можно также выявлять по ее графику. Если график функции всегда идет вверх при движении слева направо, то это указывает на монотонную возрастающую функцию. Если же график всегда идет вниз, то это указывает на монотонную убывающую функцию. Если график не меняет направление при движении слева направо, то монотонность может быть невозрастающей или неубывающей.

Монотонность является одним из основных понятий в математике, которое позволяет анализировать и описывать поведение функций на заданном промежутке. Знание о монотонности помогает решать задачи и находить экстремумы функций.

Виды монотонных функций

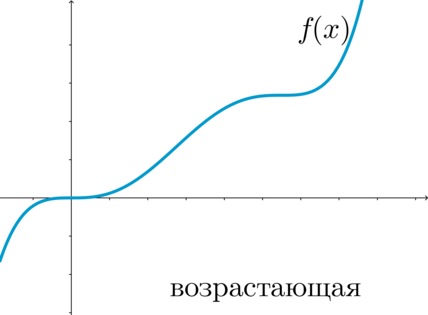
Возрастающие монотонные функции

Возрастающие монотонные функции – это функции, значения которых увеличиваются при увеличении аргумента. Такие функции имеют положительный наклон и иногда называются «строго возрастающими». Например, линейная функция y = kx, где k – положительная константа, является возрастающей монотонной функцией.

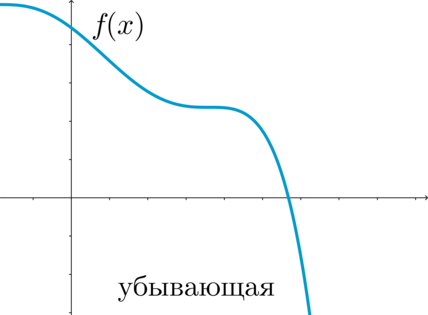
Убывающие монотонные функции

Убывающие монотонные функции – это функции, значения которых уменьшаются при увеличении аргумента. Такие функции имеют отрицательный наклон и иногда называются «строго убывающими». Например, функция y = -kx, где k – положительная константа, является убывающей монотонной функцией.

Однако, монотонные функции не обязательно должны быть строго возрастающими или строго убывающими. Возможны и кусочно-монотонные функции, которые могут быть монотонными на некоторых интервалах и немонотонными на других.

Для более подробного анализа монотонности функции может использоваться табличный метод. Таблица значений функции может помочь определить, как меняются значения функции при изменении аргумента и выявить особые точки, такие как экстремумы или точки перегиба.

Функция	Монотонность
y = x^2	Возрастает при x > 0, убывает при x < 0
y = e^x	Возрастает при любом x
y = sin(x)	Меняется от возрастания к убыванию и наоборот

Отличие монотонной функции от строго монотонной

Строго монотонная функция — это функция, которая сохраняет строгий порядок между любыми двумя точками своего области определения. То есть, если для любых двух точек x1 и x2, принадлежащих области определения функции, выполняется неравенство x1 < x2, то значение функции в точке x1 будет строго меньше значения функции в точке x2.

Таким образом, отличие монотонной функции от строго монотонной заключается в том, что монотонная функция может сохранять равенство между значениями функции в разных точках, а строго монотонная функция не может.

Знак производной функции и монотонность

В математике функция называется монотонной, если она либо всегда возрастает (т.е. ее значения строго увеличиваются при увеличении аргумента), либо всегда убывает (т.е. ее значения строго уменьшаются при увеличении аргумента).

Знак производной функции является одним из способов определить монотонность функции. Производная функции показывает, как изменяется значение функции относительно ее аргумента.

Положительная производная

Если производная функции положительна на всей области определения, то функция является строго возрастающей. Это означает, что при увеличении аргумента значение функции также возрастает.

Отрицательная производная

Если производная функции отрицательна на всей области определения, то функция является строго убывающей. Это означает, что при увеличении аргумента значение функции уменьшается.

Важно отметить, что функция может быть монотонной, но не строго монотонной. Например, если производная функции равна нулю на некотором интервале, то значит функция не меняет своего значения на этом интервале и является монотонной на нем, но не является строго монотонной.

Как определить монотонность функции на интервале?

Если производная функции положительна на всем интервале или отрицательна на всем интервале, то функция является строго монотонной на этом интервале. Если производная равна нулю во всех точках интервала, то функция может быть как монотонной, так и не монотонной на этом интервале.

Для определения строгой монотонности функции на интервале, нужно:

Найти производную функции.
Решить уравнение производной на интервале.
Построить таблицу знаков производной и найти интервалы, на которых производная сохраняет определенный знак.
Определить, как изменяется функция на каждом интервале: возрастает или убывает.

Для определения нестрогой монотонности (включая монотонность в точке) функции на интервале, нужно:

Найти производную функции.
Решить уравнение производной на интервале.
Построить таблицу знаков производной и найти интервалы, на которых производная сохраняет определенный знак.
Определить, как изменяется функция на каждом интервале и в точках перегиба: возрастает или убывает.

Теорема о монотонности функции на отрезке

Теорема о монотонности функции на отрезке гласит, что если функция $f(x)$ непрерывна на отрезке $[a, b]$ и строго монотонна на этом отрезке, то она имеет обратную функцию $f^{-1}(x)$, которая также будет непрерывна на отрезке $[f(a), f(b)]$, и будет строго монотонной на этом отрезке с тем же типом монотонности.

Другими словами, если функция на отрезке возрастает (т.е. каждое следующее значение функции больше предыдущего) или убывает (каждое следующее значение функции меньше предыдущего), то она будет иметь обратную функцию, которая также будет возрастающей или убывающей.

Эта теорема имеет важное значение в математическом анализе и обеспечивает базовое понимание свойств монотонных функций на отрезке. Она является одной из фундаментальных теорем, которая позволяет изучать поведение функций на заданном интервале.

Способы проверки монотонности функции

Существует несколько способов проверки монотонности функции:

Анализ производной. Если производная функции на всей области определения положительна, то функция монотонно возрастает. Если производная отрицательна, то функция монотонно убывает. Если производная равна нулю, то функция имеет экстремумы.
Анализ знаков разностей значений функции на интервалах. Если значения функции на интервале возрастают (то есть разность значений положительна), то функция монотонно возрастает на этом интервале. Если значения функции на интервале убывают (то есть разность значений отрицательна), то функция монотонно убывает на этом интервале.
Исследование точек перегиба и экстремумов. Эти точки могут влиять на монотонность функции. Например, функция может быть монотонно возрастающей до точки перегиба, а после нее – монотонно убывающей.
Анализ графика функции. Представление графика функции визуально позволяет определить монотонность на определенных участках.

Выбор метода проверки монотонности функции зависит от доступных данных о функции и удобства использования конкретного метода. Важно учитывать, что проверка монотонности функции может быть сложной задачей, особенно для сложных функций или функций с несколькими переменными.

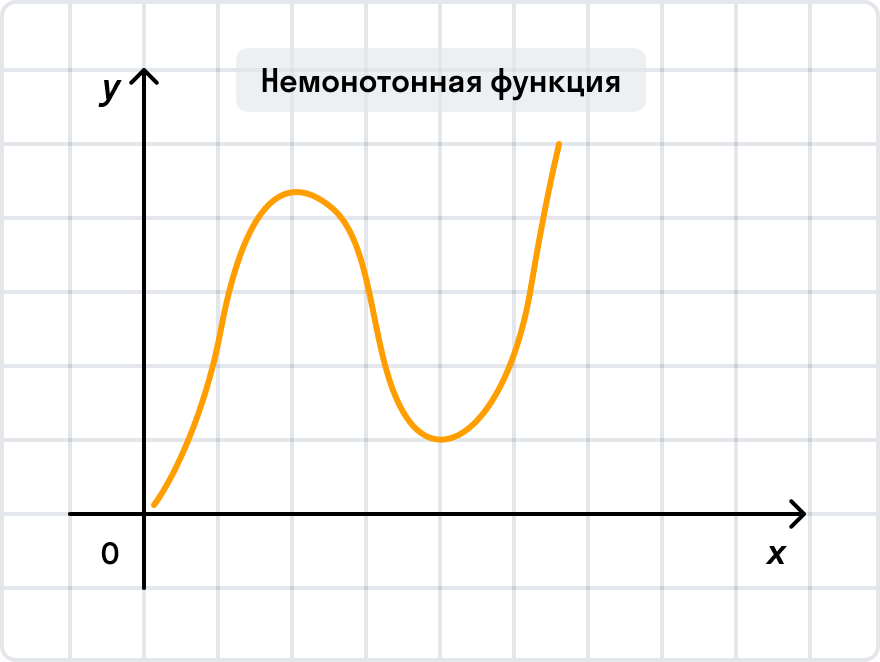
Примеры монотонных и немонотонных функций

Давайте рассмотрим примеры монотонных функций:

Линейная функция: y = kx + b, где k и b — константы. В этом случае функция всегда растет или убывает с постоянным темпом.
Экспоненциальная функция: y = a^x, где a — положительное число. Эта функция всегда возрастает при x > 0 и убывает при 0 < x < 1.
Степенная функция: y = x^n, где n — целое число. Она может быть монотонно возрастающей или монотонно убывающей, в зависимости от значения n.

Примеры немонотонных функций:

Синусоидальная функция: y = sin(x). Эта функция периодически меняет свой характер, то возрастая, то убывая, при каждом периоде.
Косинусоидальная функция: y = cos(x). Также как и синусоидальная функция, она периодически меняет свой характер, но сдвинута по фазе.
Функция с разрывами: y = 1/x. Эта функция имеет вертикальный асимптоту при x = 0, и меняет свой характер по обе стороны от нее.

Таким образом, монотонная функция имеет строго определенное направление изменения, в то время как немонотонная функция может менять свое направление несколько раз на своем графике.

Вопрос-ответ:

Что такое монотонная функция?

Монотонная функция — это функция, для которой сохраняется ее возрастание или убывание на определенном промежутке, то есть функция либо всегда возрастает, либо всегда убывает.

Какие свойства имеет монотонная функция?

Монотонная функция может иметь два свойства: возрастание и убывание. Если функция возрастает, то с увеличением значения аргумента увеличивается и значение функции. Если функция убывает, то с увеличением значения аргумента убывает значение функции.

Чем отличается монотонная функция от строго монотонной?

Монотонная функция имеет возможность сохранять свое значение в определенных точках промежутка, то есть может быть горизонтальной. Строго монотонная функция же не имеет таких точек и всегда либо возрастает, либо убывает.

Как найти интервалы возрастания и убывания монотонной функции?

Для нахождения интервалов возрастания и убывания монотонной функции нужно найти значения производной функции и решить неравенства. Если производная положительна на интервале, то функция возрастает на этом интервале, если отрицательна — функция убывает.