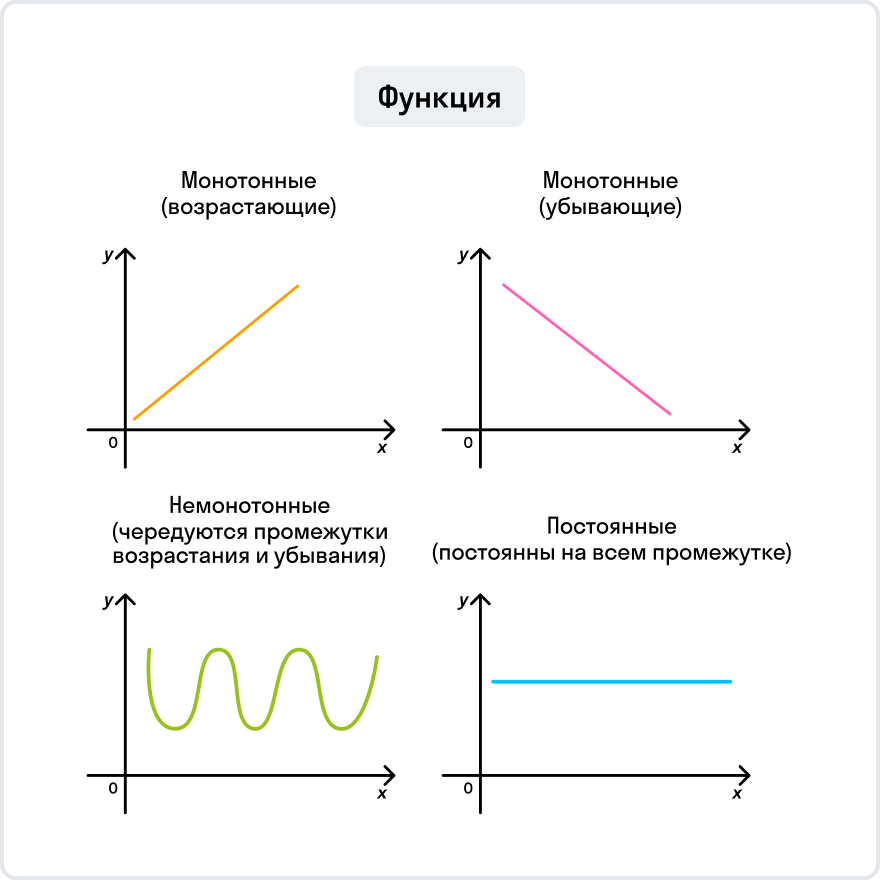
Возрастающая функция – это функция, значения которой строго возрастают при увеличении аргумента. То есть, если мы увеличиваем значение аргумента, то значение функции также увеличивается. В математике такие функции играют важную роль, поскольку они помогают описать разнообразные явления и взаимосвязи между переменными.
Определить, является ли функция возрастающей, можно с помощью анализа ее производной. Если производная функции положительна на всей области определения, то функция является возрастающей. Производная функции показывает изменение значения функции при изменении аргумента. Если производная положительна, то значение функции увеличивается.
Например, рассмотрим функцию f(x). Если при увеличении значения x значение f(x) также увеличивается, то функция f(x) является возрастающей. Это может быть проиллюстрировано графически: график функции будет иметь положительный наклон, стремящийся вверх.
Раздел 1: Определение возрастающей функции
Для формального определения возрастающей функции можно использовать математическую запись. Функция f(x) является возрастающей на интервале I, если для любых двух точек x1 и x2 в этом интервале, где x1 < x2, выполняется неравенство f(x1) < f(x2).
Это означает, что при перемещении от x1 к x2 значения функции f(x) увеличиваются. Другими словами, график функции при таком движении будет подниматься вверх.
Возрастающая функция может быть представлена в различных формах: алгебраическими выражениями, таблицами, графиками и другими математическими методами.
Примером возрастающей функции является функция f(x) = x, где значения функции увеличиваются пропорционально значению аргумента. Также квадратичная функция f(x) = x^2 является возрастающей на интервале [0, +∞), так как при увеличении аргумента значения функции становятся больше.
Понятие возрастающей функции
Чтобы определить, является ли функция возрастающей, нужно проанализировать ее график. Если график функции поднимается с левого края координатной плоскости вправо, то функция является возрастающей.
Другим способом определения возрастающей функции является вычисление производной функции. Если производная положительна на всем интервале определения функции, то это означает, что функция возрастает на этом интервале.
Возрастающие функции широко используются в различных областях математики и науки, так как их свойства позволяют моделировать и анализировать разнообразные явления и процессы.
Основные свойства возрастающих функций
Основные свойства возрастающих функций:
- Монотонность: возрастающая функция может быть монотонно возрастающей на всем области определения, то есть значение функции растет при каждом увеличении значения аргумента.
- Непрерывность: возрастающие функции обычно являются непрерывными на своем области определения, то есть график функции не имеет разрывов или перегибов.
- Ограниченность: возрастающая функция может быть ограниченной сверху или снизу на своем области определения.
- Производная: производная возрастающей функции всегда положительна на ее области определения.
- Инъективность: возрастающая функция может быть инъективной (однозначной), то есть разным значениям аргумента соответствуют разные значения функции.
Знание этих свойств позволяет анализировать и понимать поведение возрастающих функций, а также использовать их в различных приложениях, например, в экономике, физике и других науках.
Примеры возрастающих функций
| Функция | График |
|---|---|
| Линейная функция |  |
| Экспоненциальная функция |  |
| Квадратичная функция |  |
| Степенная функция |  |
Это всего лишь несколько примеров возрастающих функций. Существует множество других функций, которые также могут быть возрастающими. Важно понимать, что возрастание функции может быть нелинейным и иметь различные формы графиков.
Раздел 2: Как определить возрастающую функцию?
Первый способ — анализ производной функции. Если производная функции всюду положительна, то это означает, что функция возрастает на всем промежутке определения. Если производная нигде не равна нулю, то функция возрастает монотонно. Однако, если производная положительна на одних участках, а отрицательна на других, то функция не является строго возрастающей.
Второй способ — сравнение значений функции на разных точках. Если при увеличении значения аргумента значение функции также увеличивается, то функция является возрастающей. Например, если для любых двух точек x1 и x2, где x1 < x2, выполняется условие f(x1) < f(x2), то функция является возрастающей.
Третий способ — определение знака разности значений функции на разных точках. Если для всех точек x1 и x2, где x1 < x2, выполняется условие f(x1) — f(x2) < 0, то функция является возрастающей.
Анализ графика функции
При анализе графика функции следует обратить внимание на следующие характеристики:
- Наклон графика: если график функции стремится к верхней части координатной плоскости при увеличении аргумента, то функция называется возрастающей.
- Точки экстремума: на графике функции могут присутствовать точки минимума и максимума. Точка минимума соответствует самому низкому значению функции, а точка максимума — наивысшему. Определение точек экстремума позволяет выявить особенности функции.
- Пересечение с осями: график функции может пересекать горизонтальную ось и/или вертикальную ось. Пересечение графика с горизонтальной осью показывает значения функции при аргументе, равном нулю.
Анализ графика функции позволяет получить представление о ее поведении по мере изменения аргумента. Такой анализ позволяет лучше понять, как функция растет или убывает, в каких точках достигает экстремальных значений и как она ведет себя на интервалах между этими точками.
Подсчет производной функции
Для подсчета производной функции существует ряд правил, которые позволяют упростить задачу и провести вычисления более эффективно:
| Функция | Производная |
|---|---|
| f(x) = k | f'(x) = 0 |
| f(x) = x^n | f'(x) = n * x^(n-1) |
| f(x) = sin(x) | f'(x) = cos(x) |
| f(x) = cos(x) | f'(x) = -sin(x) |
| f(x) = e^x | f'(x) = e^x |
Это лишь небольшой набор правил, которые позволяют вычислить производную для функций различных типов. Существует и множество других формул и методов, которые могут применяться в зависимости от конкретной функции.
Подсчитав производную функции, можно изучить ее поведение, определить моменты, когда она возрастает или убывает, и понять ее основные свойства. Таким образом, производная функции играет ключевую роль в изучении и анализе возрастающих функций.
Вопрос-ответ:
Что такое возрастающая функция?
Возрастающая функция — это функция, значение которой увеличивается при увеличении аргумента. То есть, если для любых двух аргументов x1 и x2, таких что x1 < x2, значение функции f(x1) меньше значения f(x2), то функция f(x) является возрастающей.
Как определить, что функция возрастающая?
Для определения, является ли функция возрастающей, необходимо сравнить значения функции для различных аргументов. Если при увеличении аргумента значение функции также увеличивается, то функция является возрастающей. Это можно проверить, вычислив значения функции для нескольких разных аргументов.
Есть ли какие-то особенности в графике возрастающей функции?
Да, у графика возрастающей функции есть несколько особенностей. Во-первых, он стремится к бесконечности при увеличении аргумента. Во-вторых, график возрастающей функции всегда расположен выше оси абсцисс. Также график может иметь различную крутизну в зависимости от характера функции.
Может ли функция быть одновременно возрастающей и убывающей?
Нет, функция не может быть одновременно возрастающей и убывающей. Взаимоисключающими свойствами являются возрастание и убывание функции. Если функция увеличивается с ростом аргумента, то она не может одновременно уменьшаться по значению.
Как проверить, что функция является строго возрастающей?
Для проверки, является ли функция строго возрастающей, необходимо сравнить значения функции для различных пар аргументов. Если для любых двух аргументов x1 и x2, таких что x1 < x2, значение функции f(x1) меньше значения f(x2), и при этом значения функции f(x1) и f(x2) не равны, то функция f(x) является строго возрастающей.
Что такое возрастающая функция?
Возрастающая функция — это функция, значения которой увеличиваются с ростом аргумента. То есть, если для любых двух значений аргумента x1 и x2, где x1 < x2, соответствующие значения функции f(x1) и f(x2) также удовлетворяют условию f(x1) < f(x2), то функция f(x) называется возрастающей.