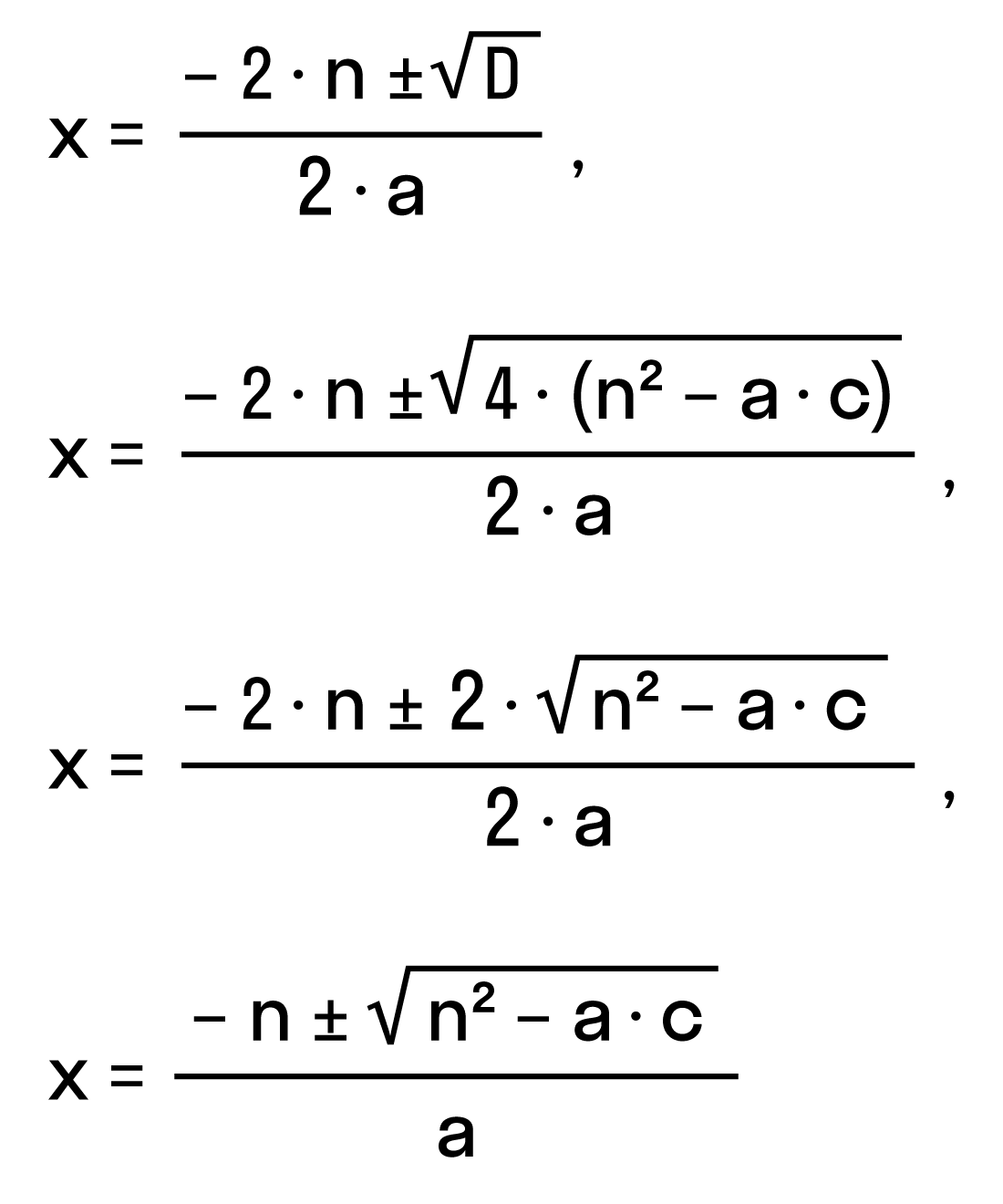
Квадратное уравнение — это уравнение вида ax^2 + bx + c = 0, где a, b и c — коэффициенты, причем a ≠ 0. Важно отметить, что старший коэффициент a при переменной x возведен в квадрат, отсюда и происходит название такого уравнения. Квадратные уравнения лежат в основе многих математических моделей и являются фундаментом для изучения алгебры и анализа.
Решение квадратного уравнения может быть найдено с использованием различных методов. Один из наиболее распространенных методов — это формула дискриминанта. Дискриминант D вычисляется по формуле D = b^2 — 4ac, где b и c — коэффициенты квадратного уравнения. Значение дискриминанта позволяет определить, сколько корней имеет уравнение и какие именно.
Если дискриминант больше нуля, то уравнение имеет два различных вещественных корня. Если дискриминант равен нулю, то уравнение имеет один вещественный корень — это так называемый кратный корень. Если дискриминант меньше нуля, то уравнение имеет два комплексных корня, которые представляют собой комплексно-сопряженные числа.
Определение и особенности квадратного уравнения
Особенности квадратного уравнения состоят в том, что оно содержит переменную в степени 2. Это означает, что график квадратного уравнения является параболой. В зависимости от коэффициентов a, b и c, парабола может быть направлена вверх или вниз, открытой вверх или вниз, или быть перевернутой. Также квадратное уравнение имеет два решения (корня), которые могут быть действительными или комплексными числами.
Корни квадратного уравнения можно найти с помощью формулы: x = (-b ± √(b^2 — 4ac)) / (2a), которая называется формулой дискриминанта. Значение дискриминанта (D = b^2 — 4ac) определяет количество и тип корней квадратного уравнения:
| Значение D | Количество корней | Тип корней |
|---|---|---|
| D > 0 | 2 различных корня | Действительные числа |
| D = 0 | 2 одинаковых корня | Действительные числа |
| D < 0 | Нет действительных корней | Комплексные числа |
Квадратные уравнения широко применяются в различных областях науки, техники и физики. Они позволяют решать задачи, связанные с нахождением неизвестных значений переменных и анализом кривых параболического характера. Понимание особенностей и способов решения квадратных уравнений является важным базисом для изучения более сложных алгебраических уравнений и математических концепций.
Что представляет собой квадратное уравнение?
ax2 + bx + c = 0,
где a, b и c – коэффициенты, причем a ≠ 0.
В квадратном уравнении переменная x входит во второй степени. Коэффициенты a, b и c могут быть любыми числами. Уравнение может иметь один, два или ноль корней.
Решение квадратного уравнения заключается в нахождении значений переменной x, которые удовлетворяют уравнению. Корни могут быть действительными числами или комплексными числами.
Квадратные уравнения широко применяются в различных областях науки и техники. Они помогают моделировать различные процессы и находить решения задач, связанных с оптимизацией, физикой, экономикой и другими дисциплинами.
Основные характеристики квадратного уравнения
1. Степень уравнения: Квадратное уравнение имеет степень 2, так как самая высокая степень переменной x равна 2.
2. Дискриминант: Дискриминант — это выражение, на основе которого мы можем определить, сколько корней имеет квадратное уравнение. Дискриминант вычисляется по формуле D = b^2 — 4ac. Если D > 0, то уравнение имеет два различных рациональных корня. Если D = 0, то уравнение имеет один рациональный корень (два совпадающих). Если D < 0, то уравнение не имеет действительных корней и решений.
3. Решения уравнения: Решения квадратного уравнения находятся с использованием формулы корней, которая связывает значения коэффициентов a, b, c и дискриминанта D. Формула имеет два решения x = (-b ± √D) / (2a). Квадратное уравнение может иметь ноль, один или два различных корня, в зависимости от значения дискриминанта и коэффициентов.
4. Симметрия графика: График квадратного уравнения представляет собой параболу. Она может быть направленной вверх, если коэффициент a положительный, или направленной вниз, если a отрицательный. Форма параболы симметрична относительно прямой, проходящей через вершину параболы, которая находится в точке (-b/2a, f(-b/2a)), где f(x) — значение функции квадратного уравнения.
Квадратные уравнения широко используются в математике, физике, экономике и других науках для моделирования реальных явлений и решения различных задач.
Как распознать квадратное уравнение?
Для того чтобы распознать квадратное уравнение, необходимо проверить, что степень уравнения равна двум и коэффициент при переменной с не равен нулю.
Например, уравнение 2x^2 + 3x — 5 = 0 — это квадратное уравнение, потому что степень уравнения равна двум, а коэффициент c при переменной x не равен нулю.
Если степень уравнения не равна двум или коэффициент при переменной x равен нулю, то это не является квадратным уравнением.
Знание того, как распознать квадратное уравнение, очень важно для правильного подхода к его решению. Решение квадратного уравнения может быть осуществлено с помощью различных методов, таких как факторизация, использование формулы квадратного корня или метода дискриминанта.
Методы решения квадратных уравнений
Существует несколько методов для решения квадратных уравнений:
1. Метод факторизации
Если возможно разложить квадратное уравнение на два линейных множителя, можно найти его корни в заданной форме. Например, уравнение $x^2 + 5x + 6 = 0$ можно переписать в виде $(x + 2)(x + 3) = 0$, откуда $x = -2$ и $x = -3$.
2. Метод использования формулы корней
Для квадратного уравнения вида $ax^2 + bx + c = 0$ можно использовать формулу корней, известную как формула дискриминанта: $x = \frac{-b \pm \sqrt{b^2 — 4ac}}{2a}$. Здесь $\pm$ показывает, что уравнение имеет два корня. Если дискриминант равен нулю, уравнение имеет один корень (два одинаковых корня), а если дискриминант отрицателен, уравнение не имеет корней.
3. Метод завершения квадрата
Если квадратное уравнение имеет вид $(x + a)^2 + b = 0$ или $(x — a)^2 + b = 0$, его можно привести к квадратному трехчлену. Устанавливая соответствующие значения, можно найти корни уравнения.
4. Метод графического представления
Квадратное уравнение может быть решено путем построения графика функции $y = ax^2 + bx + c$ и определения точек пересечения с осью $x$. Это графическое представление может визуально показать, где находятся корни уравнения.
Овладение этими методами поможет вам эффективно решать квадратные уравнения и применять их в различных математических и физических задачах.
Формула дискриминанта
Формула дискриминанта позволяет определить количество и тип корней квадратного уравнения. Она выглядит следующим образом:
$D = b^2 — 4ac$,
где $D$ — дискриминант, который является ключевым показателем при решении квадратного уравнения.
Исходя из значения дискриминанта, можно определить следующие случаи:
- Если $D > 0$, то квадратное уравнение имеет два различных корня;
- Если $D = 0$, то квадратное уравнение имеет один корень (два корня совпадают);
- Если $D < 0$, то квадратное уравнение не имеет действительных корней, так как дискриминант отрицательный.
Используя значения коэффициентов $a$, $b$ и $c$, можно вычислить значение дискриминанта и на основе его значения выполнить следующие действия для решения квадратного уравнения.
Методы решения квадратных уравнений без использования формул
Существует несколько методов, позволяющих решить квадратное уравнение без применения формул. Они основаны на математических преобразованиях и графическом представлении уравнений.
Один из таких методов – графический метод решения. Суть его заключается в построении графика функции, заданной уравнением, и определении корней уравнения по графику. Если график пересекает ось абсцисс в двух точках, то у уравнения два действительных корня. Если он пересекает ось абсцисс в одной точке, то у уравнения один корень. Если график не пересекает ось абсцисс, то у уравнения нет действительных корней.
Еще один метод решения квадратных уравнений – метод подстановки. Он заключается в поочередной подстановке различных значений переменной вместо нее в уравнение и определении, при каком значении переменной уравнение становится верным. Таким образом, можно найти все корни квадратного уравнения.
Третий метод – метод сокращенного умножения. Он заключается в преобразовании квадратного уравнения к виду (x-a)(x-b) = 0, где a и b – это некоторые числа. Затем находим корни уравнения, приравнивая каждую скобку к нулю.
Все эти методы не требуют использования формул и позволяют найти корни квадратных уравнений на основе лишь алгоритмических преобразований и методов графической интерпретации.
Примеры решения квадратных уравнений
Рассмотрим несколько примеров решения квадратных уравнений для лучшего понимания:
Пример 1:
Дано квадратное уравнение: x2 — 4x + 4 = 0
Чтобы решить это уравнение, можно использовать формулу дискриминанта: D = b2 — 4ac
Здесь коэффициенты a, b и c равны соответственно 1, -4 и 4.
Вычислим дискриминант: D = (-4)2 — 4 * 1 * 4 = 16 — 16 = 0
Так как дискриминант равен нулю, у уравнения есть только один корень.
К этому уравнению можно применить формулу корня квадратного уравнения: x = (-b ± √D) / 2a
Подставим значения коэффициентов: x = (-(-4) ± √0) / 2 * 1 = (4 ± 0) / 2 = 4 / 2 = 2
Таким образом, уравнение имеет единственное решение: x = 2
Пример 2:
Дано квадратное уравнение: x2 + 6x — 16 = 0
Вычислим дискриминант: D = 62 — 4 * 1 * (-16) = 36 + 64 = 100
Так как дискриминант больше нуля, у уравнения есть два различных корня.
Используя формулу корня квадратного уравнения, получим: x = (-6 ± √100) / 2 * 1 = (-6 ± 10) / 2 = -3 ± 5
Таким образом, уравнение имеет два решения: x = -3 + 5 = 2 и x = -3 — 5 = -8
Пример 3:
Дано квадратное уравнение: 2x2 — 7x + 3 = 0
Вычислим дискриминант: D = (-7)2 — 4 * 2 * 3 = 49 — 24 = 25
Так как дискриминант больше нуля, у уравнения есть два различных корня.
Используя формулу корня квадратного уравнения, получим: x = (7 ± √25) / 2 * 2 = (7 ± 5) / 4 = 3 / 2 или 5 / 2
Таким образом, уравнение имеет два решения: x = 3 / 2 и x = 5 / 2
Это лишь несколько примеров решения квадратных уравнений, и каждое уравнение может иметь свои особенности и специфические методы решения. Однако, использование формулы дискриминанта и формулы корня квадратного уравнения может быть полезным при решении большинства квадратных уравнений.
Вопрос-ответ:
Что такое квадратное уравнение?
Квадратным уравнением называется уравнение вида ax^2 + bx + c = 0, где a, b и c — это коэффициенты, причем a ≠ 0.
Какие методы существуют для решения квадратных уравнений?
Для решения квадратных уравнений существуют несколько методов: метод факторизации, метод использования формулы дискриминанта и метод завершения квадрата.
Как решить квадратное уравнение методом факторизации?
Для решения квадратного уравнения методом факторизации нужно разложить его на множители и приравнять каждый множитель к нулю. После этого найденные значения подставить в исходное уравнение и проверить, справедливы ли полученные равенства.
Как решить квадратное уравнение с помощью формулы дискриминанта?
Для решения квадратного уравнения с помощью формулы дискриминанта нужно вычислить значение дискриминанта по формуле D = b^2 — 4ac. Затем, если D > 0, найти корни уравнения по формулам x1 = (-b + √D) / 2a и x2 = (-b — √D) / 2a. Если D = 0, то уравнение имеет один корень x = -b / 2a. Если D < 0, то уравнение не имеет действительных корней.
Как решить квадратное уравнение методом завершения квадрата?
Для решения квадратного уравнения методом завершения квадрата нужно привести уравнение к виду (x — a)^2 = b, где a и b — числа. Затем извлечь квадратный корень из обеих частей уравнения, что приведет к двум возможным решениям: x — a = √b и x — a = -√b. Оба уравнения решаются путем добавления a к обоим частям и получения двух корней: x = a + √b и x = a — √b.