В мире математики существует большое количество понятий и терминов, которые могут вызывать затруднение у большинства людей. Одним из таких понятий являются противоположные числа. Что это такое и как они определяются?
Противоположные числа, также известные как противоположные знаки, являются числами, которые находятся на противоположных сторонах нуля на числовой прямой. Они имеют одинаковую абсолютную величину, но противоположные знаки. Например, числа 7 и -7 являются противоположными, так как их абсолютная величина равна 7, но одно число положительное, а другое — отрицательное.
Противоположные числа могут быть определены следующим образом: если дано число a, то его противоположным числом будет число -a. То есть, если у нас есть число 5, то его противоположное число будет -5. Аналогично, если дано число -3, то его противоположное число будет 3.
Противоположные числа играют важную роль в алгебре и математике в целом. Они позволяют выполнять операции сложения и вычитания с отрицательными числами, а также двигаться по числовой прямой в обоих направлениях. Понимание противоположных чисел является ключевым при работе с алгебраическими выражениями и решении уравнений.
Противоположные числа: понятие и определение
Математически противоположные числа определяются следующим образом:
| Число | Противоположное число |
|---|---|
| 5 | -5 |
| -12 | 12 |
| 0 | 0 |
| 27 | -27 |
Противоположное число обозначается унарным минусом (-) перед числом. Например, число 5 имеет противоположное число -5 и наоборот.
Противоположные числа обладают несколькими интересными свойствами:
- Сумма двух противоположных чисел всегда равна нулю.
- Разность двух противоположных чисел также равна нулю.
- Произведение противоположных чисел всегда отрицательно.
Наличие противоположных чисел позволяет осуществлять операции сложения и вычитания с легкостью и удобством.
Что такое противоположные числа
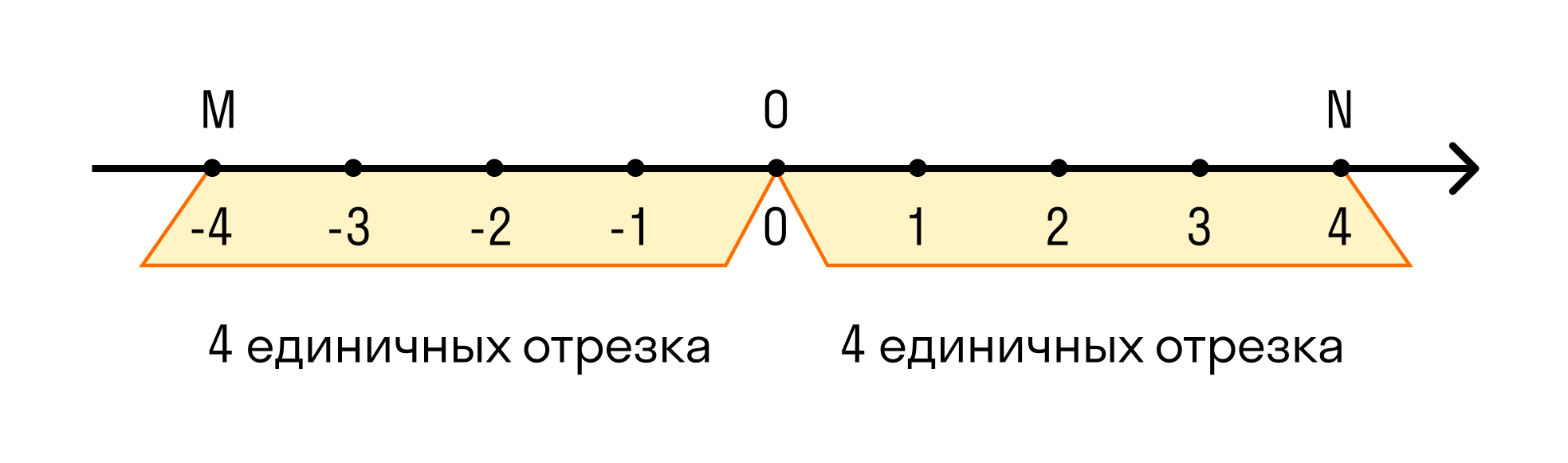
Противоположные числа могут быть представлены на числовой прямой, где центр – ноль. Любое число на противоположной стороне от нуля отображает числовой антипод. Например, число -5 расположено на числовой прямой слева от нуля и его противоположное число будет равно 5.
Свойства противоположных чисел:
- Сумма противоположных чисел всегда равна нулю. Например, 3 + (-3) = 0.
- Произведение числа на его противоположное число всегда равно минус единице. Например, 5 * (-5) = -25.
Противоположные числа играют важную роль в математике и физике, особенно при работе с алгеброй и различными видами графиков. Понимание и использование противоположных чисел помогает в решении уравнений и работы с отрицательными числами.
Определение противоположных чисел
Определение противоположных чисел может быть представлено с помощью таблицы:
| Число | Противоположное число |
|---|---|
| 5 | -5 |
| -7 | 7 |
| 0 | 0 |
Таким образом, противоположные числа являются важным концептом в математике и широко применяются в различных расчетах и операциях.
Основные свойства противоположных чисел
Основные свойства противоположных чисел включают:
- Сумма противоположных чисел всегда равна нулю. Например, 3 + (-3) = 0.
- Произведение противоположных чисел всегда равно отрицательному единицей. Например, 3 * (-3) = -9.
- Противоположное число числа a обозначается как -a.
- Если a и b — противоположные числа, то -a и -b также являются противоположными числами.
- Противоположные числа расположены на числовой оси симметрично относительно нуля.
Использование противоположных чисел позволяет выполнить операции сложения, вычитания, и умножения с отрицательными числами при сохранении основных правил арифметики.
Как определить противоположные числа
Для определения противоположного числа необходимо изменить знак числа на противоположный. Если число положительное, то для получения противоположного числа нужно поставить перед ним знак минус. Например, противоположное число для числа 5 будет -5.
Если число является отрицательным, то для получения противоположного числа нужно убрать знак минус и поставить перед ним знак плюс. Например, противоположное число для числа -2 будет +2.
Противоположные числа обладают несколькими интересными свойствами. Они располагаются симметрично относительно нулевой точки на числовой оси и их сумма всегда равна нулю. Например, если сложить число 4 и его противоположное число -4, получится 0.
Концепция противоположных чисел широко используется в математике, физике и других науках. Она помогает работать с отрицательными числами и решать различные задачи, связанные с направлениями, силами и движениями.
Знание о противоположных числах позволяет лучше понять их свойства и использовать их в практических задачах, в том числе в решении уравнений, построении графиков и анализе данных.
Метод нахождения противоположных чисел
Существует простой метод нахождения противоположного числа. Для этого нужно умножить исходное число на -1. Это можно сделать с помощью умножения числа на -1 вручную или с использованием калькулятора.
Пример:
- Противоположное число для числа 5: -1 * 5 = -5
- Противоположное число для числа -3: -1 * -3 = 3
- Противоположное число для числа 0: -1 * 0 = 0
Таким образом, для любого числа можно легко найти противоположное число, умножив его на -1.
Примеры нахождения противоположных чисел
Например:
Противоположное число для числа -5 будет 5.
Противоположное число для числа 10 будет -10.
Противоположное число для числа 0 будет также 0, так как оно не имеет знака.
Нахождение противоположных чисел осуществляется путем изменения знака числа на противоположный. Для положительного числа меняем знак на отрицательный, а для отрицательного числа – на положительный. Абсолютная величина числа остается неизменной.
Например:
Для числа -7 находим противоположное число, меняя его знак: -(-7) = 7.
Для числа 3 находим противоположное число, меняя его знак: -3.
Для числа 0 противоположное число также будет 0, так как оно не имеет знака.
Практическое применение противоположных чисел
Абстрактно понимая, противоположные числа используются в математике для выполнения операций сложения и вычитания. Например, при сложении числа с его противоположным числом, результат будет равен нулю. Это свойство противоположных чисел используется в различных областях, включая физику, экономику, технику и т. д.
Одним из примеров практического применения противоположных чисел является определение направления движения. В физике противоположные числа используются для определения направления движения объектов. Например, если движение объекта осуществляется в положительном направлении, то его противоположное число будет указывать на движение в отрицательном направлении.
В экономике и финансах также используется понятие противоположных чисел. Положительные и отрицательные числа используются для представления прибылей и убытков, доходов и расходов. Благодаря этому, можно легко отслеживать финансовое положение предприятия и проводить анализ его деятельности.
В технике противоположные числа используются для кодирования информации. Например, при использовании двоичной системы кодирования, один из битов может представлять собой противоположное число другого бита.
Таким образом, противоположные числа имеют важное практическое применение в различных областях и играют значительную роль в выполнении математических операций и анализе данных.
Применение противоположных чисел в математике
В математике противоположные числа часто используются для выполнения операций сложения и вычитания. Например, если к числу 3 прибавить его противоположное число -3, то результат будет равен нулю. Это можно записать следующим образом: 3 + (-3) = 0.
Также противоположные числа можно использовать в алгебре для упрощения выражений. Например, если нужно вычислить выражение 2x + (-x), то мы можем заменить (-x) на его противоположное число x и получить 2x — x = x.
Противоположные числа также удобны в геометрии. Например, если на числовой прямой отметить точку, соответствующую числу 5, то противоположная ей точка будет соответствовать числу -5. Таким образом, противоположные числа помогают представлять отрицательные значения на числовой прямой и в пространстве.
Вопрос-ответ:
Что такое противоположные числа?
Противоположные числа — это числа, которые находятся на одинаковом расстоянии от нуля на числовой прямой, но имеют противоположные знаки.
Как определить противоположное число?
Противоположное число определяется изменением знака данного числа на противоположный.
Например, какое число является противоположным числу 5?
Число, являющееся противоположным числу 5, равно -5. Это число находится на том же расстоянии от нуля, что и число 5, но имеет противоположный знак.
Какая сумма противоположных чисел?
Сумма противоположных чисел всегда равна нулю. Например, если сложить число 3 и его противоположное число -3, получим 0.
Зачем нужно понимать понятие противоположных чисел?
Понятие противоположных чисел важно при работе с алгеброй и арифметикой, например, при решении уравнений, сложении и вычитании чисел. Кроме того, противоположные числа используются для построения числовых систем и математических моделей.
Что такое противоположные числа?
Противоположные числа — это числа, которые находятся на противоположных сторонах от нуля на числовой оси. То есть, если одно число положительное, то его противоположным будет число с таким же значением, но отрицательным знаком, и наоборот. Например, противоположные числа: 5 и -5.