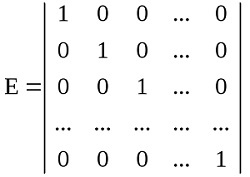
Диагональная матрица – это особая форма квадратной матрицы, у которой все элементы вне главной диагонали равны нулю. Главная диагональ – это линия элементов от верхнего левого угла до нижнего правого угла матрицы.
Такая матрица имеет свои особенности. Во-первых, она всегда является квадратной, то есть количество строк и столбцов совпадает. Во-вторых, диагональная матрица можно интерпретировать как систему линейных уравнений. Элементы главной диагонали представляют собой коэффициенты при переменных, а все остальные элементы – свободные члены.
Примером диагональной матрицы может служить матрица, в которой все элементы главной диагонали равны 1, а все остальные равны 0. Такая матрица удобна для работы с линейными уравнениями, так как позволяет осуществлять преобразования системы этих уравнений с минимальными усилиями.
Диагональные матрицы играют важную роль в различных областях математики и физики, таких как теория вероятностей, алгебраическая геометрия, квантовая механика и другие. Их использование позволяет упростить и анализировать сложные системы уравнений, а также решать разнообразные задачи, связанные с нахождением собственных значений и векторов, нахождением обратных матриц и многими другими.
Определение диагональной матрицы
Основная особенность диагональной матрицы заключается в том, что она имеет простую и удобную структуру, что позволяет эффективно выполнять определенные операции и вычисления. Благодаря своим свойствам, диагональные матрицы широко используются в различных областях математики и приложениях, включая алгебру, статистику и физику.
Диагональная матрица обладает рядом полезных свойств, например:
- Умножение диагональной матрицы на скаляр — это умножение каждого элемента матрицы на заданное число;
- Умножение двух диагональных матриц равносильно поэлементному умножению их главных диагоналей;
Таким образом, диагональные матрицы представляют собой важный инструмент в линейной алгебре и часто используются в решении многих задач и проблем.
Что такое диагональная матрица?
В линейной алгебре диагональной матрицей называется такая матрица, у которой все элементы, расположенные вне главной диагонали, равны нулю.
Это значит, что в диагональной матрице все элементы, расположенные в одной и той же позиции на главной диагонали, равны между собой, а все остальные элементы матрицы равны нулю.
Диагональные матрицы обозначаются обычно символом D или используется верхний индекс, указывающий на основное свойство матрицы – Dn, где n — размер матрицы.
Особенность диагональных матриц заключается в том, что операции над ними производятся в данном случае гораздо более просто, быстро и эффективно, поскольку множество умножений на нуль и сложений с нулем позволяют сократить количество вычислений.
Диагональные матрицы широко применяются в ряде областей, таких как теория вероятности, статистика, теория графов, численные методы и других.
Пример диагональной матрицы:
| 3 | 0 | 0 |
| 0 | 6 | 0 |
| 0 | 0 | 1 |
В данном примере все элементы матрицы, расположенные вне главной диагонали, равны нулю, что соответствует определению диагональной матрицы.
Как выглядит диагональная матрица?
Для визуализации диагональной матрицы можно использовать одну из следующих форм:
- Если элементы на главной диагонали равны диагональной матрице, можно записать ее следующим образом:
| a 0 0 | | 0 b 0 | | 0 0 c |
- Если элементы на главной диагонали имеют разные значения, можно использовать следующую форму диагональной матрицы:
| a 0 0 ... 0 | | 0 b 0 ... 0 | | 0 0 c ... 0 | | 0 0 0 ... d |
Диагональные матрицы имеют много применений в различных областях, таких как линейная алгебра, криптография и физика. В матричных операциях они облегчают вычисления и позволяют представлять различные виды данных, такие как коэффициенты линейных систем или диагональные элементы операторов.
Особенности диагональной матрицы
Основная особенность диагональной матрицы заключается в том, что она позволяет эффективно выполнять некоторые математические операции. В частности, сложение и умножение диагональных матриц между собой может быть выполнено за время, пропорциональное размеру матрицы.
Благодаря своей структуре, диагональные матрицы легко могут быть использованы для решения систем линейных уравнений и преобразований линейных пространств. Их использование позволяет упростить вычисления и снизить вычислительную сложность задачи.
Диагональные матрицы также применяются в различных областях науки и техники. Например, в теории графов они используются для описания структуры графов и моделирования различных процессов, включая транспортные, электрические и тепловые системы.
Свойства диагональной матрицы
- Главная диагональ диагональной матрицы содержит все ненулевые элементы. Все остальные элементы равны нулю.
- Диагональная матрица всегда является квадратной матрицей.
- Умножение диагональной матрицы на скаляр равносильно умножению каждого элемента матрицы на этот скаляр.
- Сумма или разность диагональных матриц также является диагональной матрицей.
- Произведение двух диагональных матриц также является диагональной матрицей. При этом на главной диагонали получаемая матрица содержит произведения элементов двух диагональных матриц.
- Обратная диагональная матрица существует только тогда, когда все элементы на главной диагонали отличны от нуля. Обратная диагональная матрица будет состоять из элементов, обратных элементам на главной диагонали и равных нулю остальные элементы.
Таким образом, диагональная матрица обладает рядом уникальных свойств, которые делают ее полезной в различных областях науки и техники.
Применение диагональных матриц
Одним из основных применений диагональных матриц является решение систем линейных уравнений. Благодаря своей простой структуре, диагональные матрицы обладают рядом удобных свойств, которые позволяют эффективно решать системы уравнений. Например, при умножении диагональной матрицы на вектор, каждый элемент вектора просто умножается на соответствующий элемент на главной диагонали. Это делает операции над системой уравнений быстрыми и простыми.
Другим применением диагональных матриц является упрощение операций в линейной алгебре. В теории матриц и операциях над ними, использование диагональных матриц может существенно упростить множество алгебраических операций, таких как умножение, сложение и взятие обратной матрицы. Благодаря этому, диагональные матрицы широко используются в различных приложениях, включая компьютерную графику, обработку сигналов, криптографию и многие другие области.
Также, диагональные матрицы часто применяются в физике для описания некоторых законов и свойств. Например, в оптике, диагональные матрицы используются для описания прохождения света через оптические системы, такие как линзы и зеркала. Они позволяют рассчитать путь, фокусировку и другие параметры света с помощью математических выражений и операций над диагональными матрицами.
В целом, диагональные матрицы являются мощным инструментом в математике и физике, обладая рядом полезных свойств и применений. Благодаря своей структуре, они позволяют эффективно решать системы линейных уравнений, упрощать операции в линейной алгебре и описывать различные явления в физике.
Вопрос-ответ:
Что значит, что матрица диагональная?
Матрица называется диагональной, если все ее элементы вне главной диагонали (то есть не лежащие на главной диагонали) равны нулю.
Как можно определить, что матрица диагональная?
Для определения матрицы на диагональность нужно проверить, что все элементы вне главной диагонали равны нулю. Если это условие выполняется, то матрица является диагональной.
Какие особенности у диагональных матриц?
Особенностью диагональных матриц является то, что операции над ними выполняются очень быстро, так как для сложения и умножения необходимо работать только с элементами на главной диагонали. Также, диагональные матрицы обладают определенной алгебраической красотой и находят применение в различных областях, включая линейную алгебру, физику и программирование.
Какие операции можно выполнять с диагональными матрицами?
С диагональными матрицами можно выполнять операции сложения и умножения. При сложении диагональных матриц просто складываются соответствующие элементы на главной диагонали. При умножении диагональных матриц элементы на главной диагонали перемножаются, остальные элементы обнуляются. Также, можно выполнять операции нахождения определителя, транспонирования и обратной матрицы для диагональных матриц.
Что такое диагональная матрица?
Диагональная матрица — это такая матрица, у которой все элементы, кроме элементов, расположенных на главной диагонали, равны нулю. То есть все элементы, находящиеся на одной линии с главной диагональю, равны нулю.