Вектор – это физическая величина, которая имеет как величину, так и направление. Векторы широко используются в различных областях науки и техники и представляют собой удобный математический инструмент для описания и анализа различных явлений и процессов.
Особенностью вектора является его направленность, которая определяет, в каком направлении действует или движется физическое явление. Векторы могут быть представлены в виде стрелок, которые указывают на направление вектора и отражают его величину по длине стрелки. Направление вектора обычно обозначается углом или с помощью точки направления на плоскости.
Векторы обладают несколькими важными свойствами. Например, векторы могут быть сложены и умножены на число, что позволяет решать сложные задачи на основе простых операций. Также векторы могут быть равными или неравными друг другу, в зависимости от их величины и направления.
Вектор: определение и примеры
Векторы используются в различных областях, например, в физике, где они описывают движение тела, а также в графике и компьютерной графике для представления направления и силы.
Одним из примеров вектора является вектор скорости. Он описывает направление и величину движения тела. Например, при движении автомобиля, скорость может быть представлена вектором, указывающим направление движения и его величину.
Другим примером является вектор силы. Он используется для описания силы, действующей на объект. Например, при анализе механических систем, вектор силы может указывать направление и величину силы, действующей на тело.
Векторы имеют особенность: они могут быть складываться и вычитаться друг из друга. Также, они могут быть умножены на число, изменяя свою величину, но сохраняя направление.
Определение вектора
Вектор в математике представляет собой направленный отрезок, который характеризуется величиной и направлением. Он может быть представлен в виде стрелки, указывающей на конец отрезка. Векторы часто используются для описания движения, силы или других физических величин.
Векторы могут быть двухмерными или трехмерными. Двухмерные векторы имеют два компонента: горизонтальный (или короткий) и вертикальный (или длинный). Каждый компонент может быть положительным или отрицательным, в зависимости от направления вектора. Трехмерные векторы имеют три компонента: горизонтальный, вертикальный и глубинный.
Векторы могут быть представлены как координатами, например (x, y) или (x, y, z), где x, y и z — компоненты вектора. Векторы также могут быть представлены векторным обозначением, например →AB, где А и В — начальная и конечная точки вектора соответственно.
Векторы могут быть сложены или вычитаны, умножены на число или умножены на другой вектор. Они также могут быть использованы для решения уравнений и задач геометрии.
Особенностью векторов является то, что они сохраняются при параллельном переносе. Это означает, что вектор не изменяется при изменении его начальной точки. Векторы также могут быть нормализованы, что означает, что их длина равна 1. Нормализованные векторы часто используются для определения направления без учета его величины.
Примеры векторов
Векторы широко применяются в различных областях, включая физику, математику, информатику и дизайн. Рассмотрим некоторые примеры векторов:
| Пример | Описание |
|---|---|
| Сила | В физике сила может быть представлена вектором, который указывает направление и величину силы. |
| Скорость | Вектор скорости описывает направление и скорость движения объекта. |
| Ускорение | Вектор ускорения определяет изменение скорости во времени. |
| Сила тяжести | Сила тяжести является вектором, направленным вниз, и определяет притяжение массы к центру Земли. |
| Векторное поле | Векторное поле представляет собой функцию, которая каждой точке в пространстве сопоставляет вектор. |
Это лишь некоторые примеры векторов, и их применение может быть гораздо шире. Векторы являются одним из важных инструментов для анализа и решения задач в различных областях.
Особенности вектора
Векторы обладают свойством суммирования. Это значит, что два или более вектора можно сложить, чтобы получить новый вектор. При этом, сумма векторов может иметь другое направление и длину, чем исходные векторы.
Еще одной особенностью вектора является то, что он может быть умножен на число, называемое скаляром. Умножение вектора на скаляр приводит к изменению его длины, но направление остается неизменным.
Векторы используются в различных областях науки, таких как физика, математика и компьютерная графика. Векторы позволяют описывать и анализировать такие физические величины, как скорость, сила, перемещение и многие другие.
Свойства векторов
Векторы в математике обладают рядом особенностей, которые делают их удобными и применимыми в различных сферах. Рассмотрим несколько основных свойств векторов.
1. Направление и длина: каждый вектор имеет определенное направление и длину. Направление вектора задается его углом относительно определенной оси или другого вектора. Длина вектора определяется его модулем и указывает на его величину.
2. Равенство векторов: два вектора считаются равными, если они имеют одинаковую длину и направление. Равенство векторов можно проверить путем сравнения их компонентов или с помощью геометрических методов.
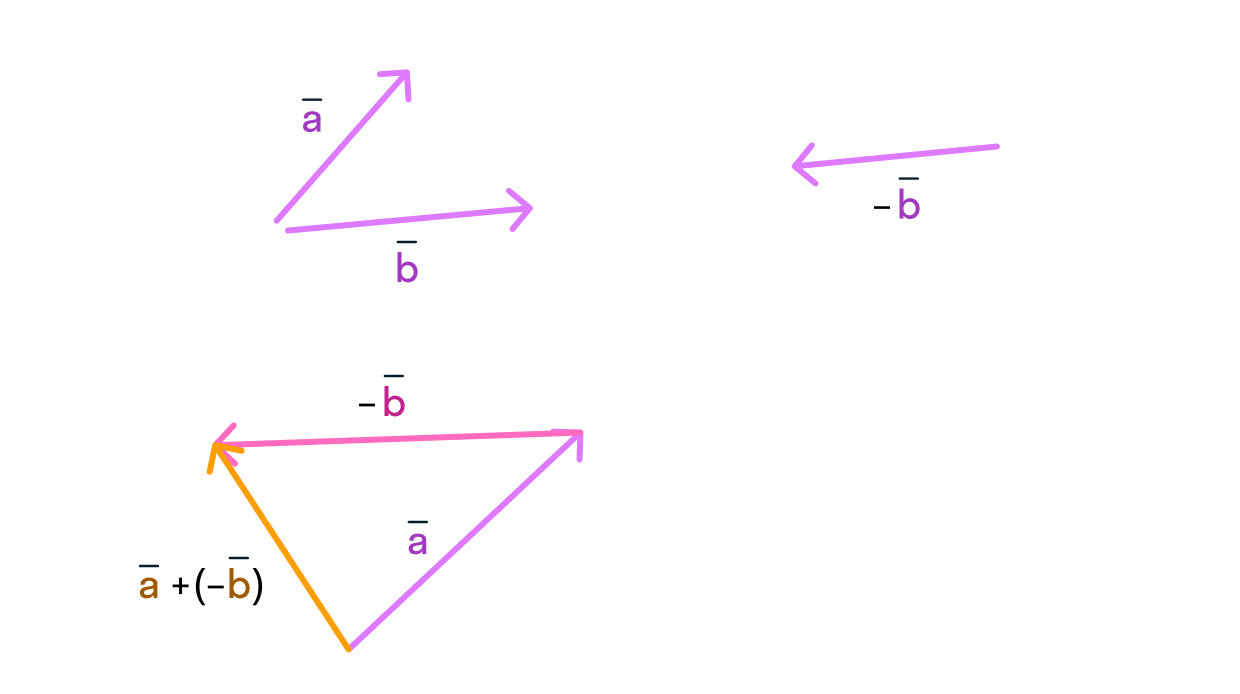
3. Сложение и вычитание: векторы можно складывать и вычитать. При сложении векторов их компоненты суммируются поэлементно, а при вычитании — вычитаются. Результатом сложения или вычитания векторов является новый вектор, который имеет длину и направление, определяемые по правилам сложения соответствующих компонент векторов.
4. Умножение вектора на число: вектор можно умножить на число. При умножении вектора на скаляр, каждая компонента вектора умножается на указанное число. Результатом умножения является новый вектор, который имеет измененную длину и может изменить направление в зависимости от знака умножаемого числа.
5. Нулевой вектор: существует особый вектор — нулевой вектор, который имеет нулевую длину и не имеет направления. Нулевой вектор обозначается символом 0 и является нейтральным элементом относительно сложения векторов.
Векторы являются важным инструментом в математике и физике, использование их свойств позволяет решать различные задачи и моделировать различные явления.
Сложение векторов
Для сложения векторов необходимо учитывать их направление и величину. Векторы, направленные в одну сторону, складываются путем суммирования их величин. Если векторы направлены в противоположные стороны, то мы вычитаем их величины.
При сложении, каждый вектор представляется в виде двух компонент: горизонтальной и вертикальной. Для получения результата складываем горизонтальные компоненты векторов и вертикальные компоненты отдельно. Полученные значения становятся компонентами результирующего вектора.
Операция сложения векторов также может быть представлена графически. Для этого на плоскости строятся векторы с учетом их направления и величины. Затем, концы векторов соединяются линией. Длина и направление линии соединения служат для получения результирующего вектора.
Сумма векторов может иметь особые свойства: ассоциативность и коммутативность. Ассоциативность означает, что порядок сложения векторов не важен — результат будет одинаковым. Коммутативность подразумевает, что перестановка векторов не изменит результат сложения.
Операция сложения векторов применяется во многих областях науки и техники, таких как физика, геометрия, компьютерная графика и других.
Умножение векторов
Скалярное умножение векторов также называется скалярным произведением или скалярным добутком. Результатом скалярного умножения двух векторов является скалярная величина. Формула скалярного умножения векторов a и b выглядит следующим образом: a · b = |a| |b| cos(α), где |a| и |b| – модули векторов a и b, α – угол между ними.
Векторное умножение векторов также называется векторным произведением или векторным добутком. Результатом векторного умножения двух векторов является новый вектор, перпендикулярный плоскости, в которой лежат исходные векторы. Формула векторного умножения векторов a и b выглядит следующим образом: a × b = |a| |b| sin(α) n, где n – единичный вектор, перпендикулярный плоскости, в которой лежат a и b.
Смешанное умножение векторов выполняется только в трехмерном пространстве и позволяет получить число, называемое смешанным произведением векторов. Формула смешанного умножения векторов a, b и c выглядит следующим образом: (a × b) · c = a · (b × c).
Умножение векторов имеет множество применений в физике, геометрии и других науках. С его помощью можно решать задачи, связанные с нахождением площади параллелограмма, объема параллелепипеда, определением направлений и величин физических величин и многое другое.
Применение векторов
В физике, векторы применяются для описания физических величин, таких как скорость, ускорение и сила. Они имеют не только численное значение, но и направление, что делает их особенно полезными при анализе движения и взаимодействия тел. Векторы позволяют не только задать величину и направление физической величины, но и выполнять операции над ними, такие как сложение и умножение на число.
В математике, векторы используются для решения различных задач. Они могут быть использованы для определения координат точек в пространстве, построения графиков функций и нахождения решений уравнений. Векторные пространства являются основой для многих математических концепций, таких как линейная алгебра и анализ.
В информатике, векторы находят применение в компьютерной графике и обработке изображений. Они могут быть использованы для хранения, передачи и обработки данных, таких как изображения, звуки и видео. Векторные алгоритмы позволяют выполнять сложные операции с графическими объектами, такие как их вращение, масштабирование и искажение.
Применение векторов не ограничивается вышеуказанными областями. Векторы также используются в экономике, социологии, биологии и других научных исследованиях. Изучение векторов и понимание их особенностей позволяет сделать новые открытия и решить сложные задачи в различных областях знаний.
Вопрос-ответ:
Что такое вектор?
Вектор — это математический объект, который характеризуется величиной и направлением. Векторы используются для представления физических величин, таких как сила или скорость, а также для решения различных задач в математике и физике.
Какие особенности у векторов?
У векторов есть несколько особенностей. Во-первых, они имеют направление, то есть указывают, куда именно направлены физические величины. Во-вторых, они имеют длину, которая определяет величину этой величины. В третьих, векторы могут складываться и вычитаться, а также умножаться на число.
Где используются векторы?
Векторы находят применение в самых различных областях. Они используются в физике для представления силы, скорости, ускорения и других физических величин. В математике они применяются для решения задач геометрии, анализа и алгебры. Кроме того, векторы используются в компьютерной графике, программировании и других областях информационных технологий.
Как складываются векторы?
Для сложения двух векторов их начало ставится в одну точку, а концы — в другую. Таким образом, получается новый вектор, называемый суммой векторов. Его направление и длина зависят от направления и длины исходных векторов. Сложение векторов выполняется по правилу параллелограмма или треугольника, в зависимости от вида параллельных пересекающихся граней, на которых лежат исходные векторы.
Что такое нулевой вектор?
Нулевой вектор — это вектор, у которого длина равна нулю. Такой вектор не имеет направления и не может быть использован для представления физических величин. Нулевой вектор служит нейтральным элементом при сложении векторов, так как его сумма с любым вектором равна этому вектору.