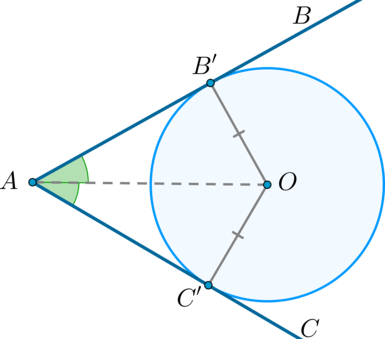
В мире геометрии существует множество интересных фигур, и одной из них является вписанный многоугольник в окружность. Эта конструкция, полученная путем соединения вершин многоугольника с центром окружности, имеет свои особенности и свойства, которые делают ее уникальной.
Определение вписанного многоугольника в окружность заключается в том, что все вершины многоугольника лежат на окружности, а его стороны являются хордами этой окружности. Число вершин в таком многоугольнике может быть любым, начиная от трех.
Интересно, что вписанный многоугольник обладает рядом интересных свойств. Например, если соединить середины двух смежных сторон вписанного многоугольника, то получится многоугольник, вписанный в половину исходного. Кроме того, сумма всех углов вписанного многоугольника всегда равна 360 градусов, что делает его замечательным объектом изучения.
Что такое вписанный многоугольник в окружность?
Вписанные многоугольники обладают рядом интересных свойств и связей с окружностями. Например, диагонали вписанного многоугольника пересекаются в одной точке, называемой центром окружности. Этот центр также является центром симметрии всего многоугольника.
Вписанные многоугольники широко применяются в геометрии и математике, так как они обладают множеством полезных свойств и являются основой для дальнейших исследований в этой области.
Определение вписанного многоугольника в окружность
У вписанного многоугольника есть несколько свойств:
- Сумма всех углов вписанного многоугольника равна (n-2) * 180 градусов, где n — количество вершин многоугольника.
- Противоположные углы вписанного многоугольника равны.
- Сумма противоположных углов вписанного многоугольника также равна 180 градусов.
- Любая диагональ вписанного многоугольника является радиусом окружности.
- Вписанный многоугольник обладает наименьшей площадью среди всех многоугольников, имеющих одинаковое число сторон и описанных окружностей.
Также вписанный многоугольник в окружность является основой для данной темы, так как многие свойства и формулы, связанные с окружностью, строятся и применяются именно на основе вписанных многоугольников.
Вписанный многоугольник
Основные свойства вписанного многоугольника:
1. Сумма всех его углов равна 180 градусам. Это свойство следует из теоремы о сумме углов многоугольника. Каждый внутренний угол вписанного многоугольника будет меньше 180 градусов. Например, для треугольника на окружности, сумма углов будет равна 180 градусов.
2. Вписанный угол равен половине центрального угла, стягивающего дугу, на которой лежит вершина многоугольника. Вписанный угол образуется двумя сторонами многоугольника, которые содержат вершину и соответствующую дугу окружности. Центральный угол образуется двумя радиусами, стягивающими дугу окружности. Вписанный угол всегда половина центрального угла. Например, если центральный угол равен 120 градусам, то вписанный угол будет равен 60 градусам.
3. Длины сторон вписанного многоугольника зависят от радиуса окружности и центрального угла. Длина каждой стороны вписанного многоугольника зависит от радиуса окружности и центрального угла, стягивающего дугу, на которой лежит эта сторона. Чем больше радиус или центральный угол, тем длиннее стороны многоугольника. Например, если радиус окружности больше, то длины сторон вписанного треугольника также будут больше.
Вписанный многоугольник имеет множество интересных свойств и применений в геометрии и математике. Он широко используется для решения задач и доказательств теорем. Изучение вписанных многоугольников помогает понять основные законы и свойства окружности.
Окружность
Окружность является одной из основных геометрических фигур и обладает рядом характеристических свойств. Например, диаметр окружности — это отрезок, соединяющий две точки на окружности, и который проходит через ее центр.
Исследование окружности и вписанных в нее фигур является одной из важных задач геометрии и находит множество приложений в различных областях. Окружность часто используется в строительстве, математическом моделировании и даже в искусстве.
Эта геометрическая фигура обладает особым эстетическим и символическим значением, привлекая внимание и вдохновляя на творчество.
Определение вписанного многоугольника в окружность
Описание
Вписанный многоугольник в окружность является особым случаем многоугольника, в котором все точки многоугольника равноудалены от центра окружности. Таким образом, радиус окружности будет равен расстоянию от центра до каждой вершины многоугольника.
Важно отметить, что вписанный многоугольник имеет ряд свойств, таких как:
- Сумма всех углов вписанного многоугольника равна (n-2) * 180 градусов, где n — количество вершин многоугольника.
- Углы, образованные сторонами многоугольника и прямыми, проведенными от центра окружности к его вершинам, являются прямыми углами.
- Длина каждого отрезка, соединяющего вершину многоугольника с центром окружности, будет равной радиусу окружности.
Изучение вписанного многоугольника в окружность имеет большое значение в геометрии, а также находит применение в различных областях науки и техники, таких как строительство, колесницы и дизайн.
Свойства вписанного многоугольника в окружность
Вписанный многоугольник в окружность обладает несколькими важными свойствами:
1.Хорды, соединяющие вершины вписанного многоугольника, равны между собой:
Если в многоугольнике провести хорды (отрезки, соединяющие вершины многоугольника) и эти хорды равны между собой, то многоугольник называется вписанным в окружность.
2.Углы, опирающиеся на одну и ту же дугу окружности, равны между собой:
В вписанном многоугольнике углы, центры которых лежат на одной и той же дуге окружности, равны между собой. Это свойство называется «углами на дуге».
3.Сумма противолежащих углов в вписанном многоугольнике равна 180 градусам:
В вписанном многоугольнике сумма двух противолежащих углов всегда равна 180 градусам. Обозначается этот факт как «сумма противолежащих углов».
4.Биссектрисы углов в вписанном многоугольнике являются радиусами окружности:
В вписанном многоугольнике биссектрисы любых углов пересекаются в центре окружности, а также являются радиусами этой окружности. Это свойство помогает найти радиус вписанной окружности по биссектрисе угла.
Теорема о центральном угле
Вписанный многоугольник в окружность обладает рядом интересных свойств, одно из которых называется теоремой о центральном угле. Эта теорема устанавливает связь между центральными углами и дугами окружности, образованными этими углами.
Формулировка теоремы:
Если угол с вершиной, лежащей на окружности, отличен от прямого, то дуга, образованная этим углом и лежащая на окружности, также отличается от полного оборота на этот угол.
| Центральный угол
| Дуга окружности, соответствующая центральному углу
|
Теорема о центральном угле позволяет более углубленно изучить свойства вписанных многоугольников в окружность и использовать их в решении различных геометрических задач.
Теорема о равных углах
Теорема: В вписанном многоугольнике в окружность, углы, опирающиеся на одну и ту же дугу, равны между собой.
Доказательство:
Пусть у нас есть вписанный многоугольник в окружность и два угла, опирающиеся на одну и ту же дугу. Предположим, что эти углы не равны между собой.
Обозначим эти углы как A и B, а дугу, на которую они опираются — как AB.
Проведем диаметр AC, который делит многоугольник на две части.
Рассмотрим треугольник ABC:
— Углы в вершине B и C являются прямыми, так как они составляют часть диаметра. Значит, B + C = 180°.
— Угол A является внутренним углом многоугольника, а значит, он меньше 180°.
Из этих двух уравнений можно заключить, что B + C > 180°, что противоречит сумме углов в треугольнике.
Таким образом, предположение о том, что углы A и B не равны между собой, является неверным.
Следовательно, углы, опирающиеся на одну и ту же дугу в вписанном многоугольнике, всегда равны между собой.
Теорема о равенстве дуг
Теорема о равенстве дуг утверждает, что если вписанный многоугольник в окружность имеет две равные дуги, то соответствующие им углы в многоугольнике также равны.
Другими словами, если в окружности имеются две дуги, делящие ее на две равные части, то углы, опирающиеся на эти дуги, будут равными.
Доказательство данной теоремы можно провести следующим образом:
- Рассмотрим вписанный многоугольник в окружность.
- Пусть даны две равные дуги на этой окружности.
- Проведем прямую, проходящую через центр окружности и точки пересечения этих дуг.
- Так как дуги равны, то прямая будет проходить через центр окружности и, следовательно, делить ее пополам.
- Углы, опирающиеся на эти дуги, будут соответствовать равенству дуг и, следовательно, будут равными.
Таким образом, теорема о равенстве дуг позволяет нам утверждать, что в вписанном многоугольнике, где имеются две равные дуги на окружности, соответствующие углы также будут равными.
Вопрос-ответ:
Что такое вписанный многоугольник в окружность?
Вписанный многоугольник в окружность — это многоугольник, все вершины которого лежат на окружности.
Как найти радиус вписанной окружности?
Радиус вписанной окружности можно найти по формуле: r = a / (2 * tg(π / n)), где a — длина стороны многоугольника, n — количество сторон.
Как доказать, что многоугольник вписан в окружность?
Для доказательства, что многоугольник вписан в окружность, достаточно доказать, что все его вершины лежат на окружности. Это можно сделать, вычислив расстояние от каждой вершины до центра окружности и убедившись, что оно равно радиусу окружности.
Как найти площадь вписанного многоугольника?
Площадь вписанного многоугольника можно найти по формуле: S = (n * a * R^2 * sin(2π / n)) / 2, где n — количество сторон многоугольника, a — длина стороны, R — радиус вписанной окружности.

