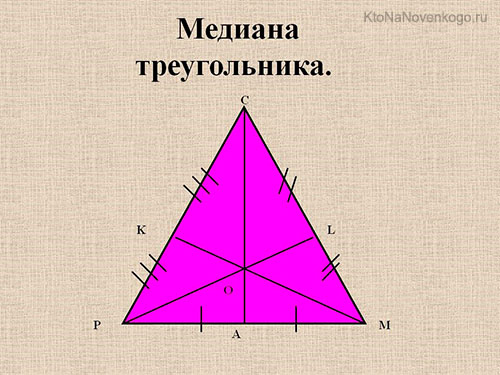
Медиана треугольника — это особая линия, которая соединяет вершину треугольника с серединой противолежащей стороны. Таким образом, в треугольнике всегда существует три медианы, каждая из которых соединяет вершину с серединой соответствующей стороны.
Медианы треугольника имеют ряд интересных свойств и применяются в различных областях науки и практики. Одним из самых известных свойств медианы является то, что они пересекаются в одной точке. Это особое место пересечения называется центром тяжести или центром масс треугольника.
Медианы также позволяют найти площадь треугольника. Для этого достаточно провести медиану и измерить ее длину. Площадь треугольника будет равна половине произведения длины медианы и длины соответствующей ей стороны треугольника.
Определение медианы треугольника
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Точка пересечения медиан треугольника называется центром тяжести.
Медианы треугольника равны между собой и делятся центром тяжести в отношении 2:1. То есть, если a, b и c — длины сторон треугольника, то длина медианы, проведенной из вершины к противоположной стороне, равна:
| Медиане из вершины A | : | 2√(2b^2 + 2c^2 — a^2) |
| Медиане из вершины B | : | 2√(2a^2 + 2c^2 — b^2) |
| Медиане из вершины C | : | 2√(2a^2 + 2b^2 — c^2) |
Медианы треугольника играют важную роль в его геометрии. Они не только соединяют вершины треугольника со своим центром тяжести, но также делят его на три равные части. Медианы также могут использоваться для нахождения площади треугольника и его высот.
Геометрическое свойство медианы
Когда мы проводим медиану к вершине треугольника, она делит противоположную сторону на две равные части. Также, медиана делит площадь треугольника пополам: одна половина площади треугольника находится ниже медианы, а другая — выше.
Данное геометрическое свойство медианы можно доказать при помощи различных методов, включая метод аналитической геометрии и метод подобия треугольников.
Примечание: Медианы могут пересекаться в одной точке, которая называется центром тяжести треугольника. Центр тяжести является точкой пересечения всех трех медиан треугольника.
Расчет медианы треугольника
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Медианы обозначаются строчными буквами: m_a, m_b и m_c.
Поиск координат середин сторон треугольника
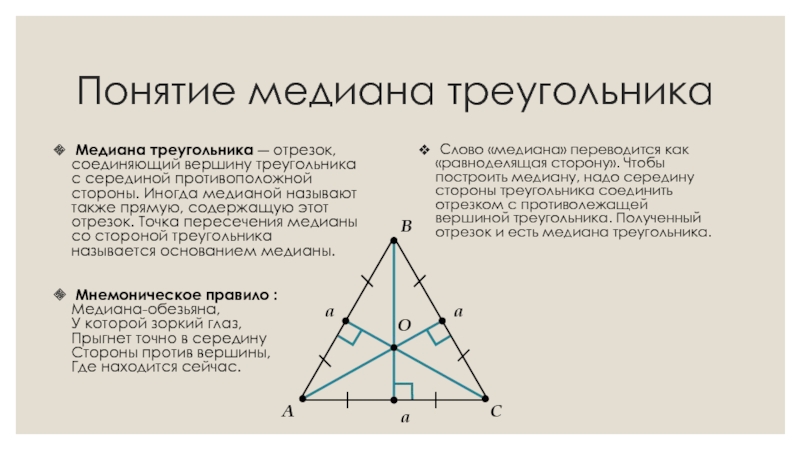
Для расчета медианы треугольника необходимо знать координаты его вершин. Прежде чем начинать вычисления медиан, найдем середины сторон треугольника. Для этого суммируем координаты вершин на каждой стороне и делим результат на 2.
Пусть координаты вершин треугольника A(x_1, y_1), B(x_2, y_2) и C(x_3, y_3). Тогда координаты середин сторон будут:
M_a = \left(\frac{x_2 + x_3}{2}, \frac{y_2 + y_3}{2}
ight)
M_b = \left(\frac{x_1 + x_3}{2}, \frac{y_1 + y_3}{2}
ight)
M_c = \left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}
ight)
Расчет медиан треугольника
Медианы треугольника можно вычислить, зная координаты середин сторон.
Медиана, проведенная из вершины A, соответствует отрезку M_bM_c. Медиана, проведенная из вершины B, соответствует отрезку M_aM_c. Медиана, проведенная из вершины C, соответствует отрезку M_aM_b.
Формулы для вычисления медиан треугольника:
m_a = \sqrt{{\left(x_1 — \frac{x_2 + x_3}{2}
ight)}^2 + {\left(y_1 — \frac{y_2 + y_3}{2}
ight)}^2}
m_b = \sqrt{{\left(x_2 — \frac{x_1 + x_3}{2}
ight)}^2 + {\left(y_2 — \frac{y_1 + y_3}{2}
ight)}^2}
m_c = \sqrt{{\left(x_3 — \frac{x_1 + x_2}{2}
ight)}^2 + {\left(y_3 — \frac{y_1 + y_2}{2}
ight)}^2}
Где \sqrt{} — корень квадратный.
Связь медианы с другими сторонами треугольника
Связь медианы с другими сторонами треугольника можно выразить с помощью различных соотношений. Например, длина медианы, проведенной из вершины треугольника к середине противоположной стороны, равна половине длины этой стороны. Это можно записать следующим образом:
МA = 1/2 BC
где М – середина стороны BC, A – вершина треугольника, MA – медиана, проведенная из вершины A.
Также можно выразить соотношение между медианами и сторонами треугольника. Например, сумма длин двух медиан треугольника, проведенных из одной и той же вершины, равна половине длины третьей стороны. Это можно записать следующим образом:
MA + MB = 1/2 AB
где A, B – вершины треугольника, MA, MB – медианы, проведенные из вершин A и B, AB – третья сторона треугольника.
Такие связи медиан с другими сторонами треугольника позволяют выполнять различные геометрические преобразования и решать задачи на нахождение неизвестных величин.
Применение медианы в практике
1. Определение центра тяжести
Медианы треугольника пересекаются в точке, известной как центр тяжести треугольника. Эта точка имеет свойство равномерно распределять массу треугольника, что делает ее полезной в различных инженерных и конструкционных задачах. Например, при проектировании строительных конструкций или распределении нагрузки в механизмах медианы могут помочь определить оптимальное распределение веса.
2. Разделение треугольника на равные части
Одно из практических применений медианы треугольника заключается в разделении треугольника на равные части. Если провести медианы из вершин треугольника, они будут пересекаться в одной точке, которая делит каждую медиану на две равные части. Это можно использовать для построения треугольника с заданными пропорциями или разделения площади треугольника на равные части для различных целей, например, в геодезии или графическом дизайне.
Итак, медиана треугольника имеет широкий спектр практического применения в различных областях, от инженерии до графического дизайна. Понимание свойств и использование медианы позволяет решать разнообразные задачи, связанные с треугольниками.
Медиана и площадь треугольника
Площадь треугольника можно найти, используя медианы. Формула для нахождения площади треугольника по медианам выглядит следующим образом:
Формула площади треугольника по медианам:
| S = (4/3) * √(p * (p — m1) * (p — m2) * (p — m3)) |
где S — площадь треугольника, m1, m2, m3 — длины медиан, p — полупериметр треугольника (p = (m1 + m2 + m3) / 2).
Медианы треугольника играют важную роль при нахождении его площади и изучении его свойств. Они также используются в различных задачах геометрии и при решении задач треугольников.
Особенности медианы в различных типах треугольников
Одна из особенностей медианы заключается в том, что она всегда пересекается с другой медианой в точке, которая делит ее в соотношении 2:1. Такая точка называется центром тяжести или барицентром треугольника.
В разных типах треугольников медиана имеет свои особенности:
| Тип треугольника | Особенности медианы |
|---|---|
| Равносторонний | Медиана является высотой, биссектрисой и медианой одновременно. Она делит треугольник на три равные части. |
| Прямоугольный | Медиана, проведенная из вершины прямого угла, является половиной гипотенузы. |
| Остроугольный | Медиана пересекается с ортоцентром треугольника в одной точке. |
| Тупоугольный | Медиана не лежит внутри треугольника, а пересекается с продолжениями сторон в точке, расположенной за его пределами. |
Медиана является важным элементом треугольника, используемым как в геометрии, так и в строительстве и других областях. Знание особенностей медианы в разных типах треугольников помогает лучше понять его свойства и применять их на практике.
Вопрос-ответ:
Что такое медиана треугольника?
Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Зачем нужна медиана треугольника?
Медиана треугольника используется в геометрии и математике для решения различных задач и определения свойств треугольника.
Как найти медиану треугольника?
Медиана треугольника находится путем соединения вершины треугольника с серединой противоположной стороны.
Сколько медиан может быть у треугольника?
У треугольника всегда есть три медианы, так как каждая вершина соединяется с серединой противоположной стороны.
Какое свойство имеет медиана треугольника?
Одно из свойств медианы треугольника заключается в том, что три медианы пересекаются в одной точке, называемой центром тяжести или барицентром треугольника.
Что называют медианой треугольника?
Медианой треугольника называется отрезок, который соединяет вершину треугольника с серединой противоположной стороны в этом треугольнике.
Как вычислить медиану треугольника?
Чтобы вычислить медиану треугольника, нужно найти середину противоположной стороны, а затем соединить эту середину с вершиной треугольника, с которой она не соединена. Медианы всегда пересекаются в одной точке, называемой центром тяжести треугольника.