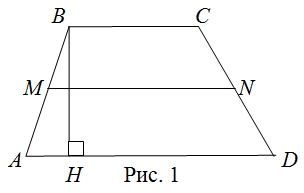
Трапеция – это особый вид четырехугольника, который имеет две параллельные стороны. Они называются основаниями. Остальные две стороны называются боковыми сторонами. Трапеция также имеет две парами углов: верхние и нижние, противоположные друг другу.
Основания трапеции могут быть разной длины, что придает ей особые свойства. Например, параллельные основания делают трапецию удобной для изучения и применения в геометрических задачах. Еще одно важное свойство трапеции заключается в том, что сумма длин ее оснований всегда равна сумме длин боковых сторон. Это можно выразить следующим равенством: a + b = c + d, где a и b – длины оснований, c и d – длины боковых сторон.
Примером трапеции может служить боковая сторона пирамиды, которая имеет разные длины у оснований. Также можно представить схему дома, где крыша является трапецией, а боковые стороны – это стены. Трапеции встречаются в архитектуре, конструировании, геодезии и многих других областях.
Определение трапеции
Трапеция также может быть классифицирована как прямоугольная, когда у нее одно из оснований является перпендикуляром к боковым сторонам. Она также может быть равнобедренной, если у нее параллельные стороны одинаковой длины.
Основные свойства трапеции:
- У трапеции сумма углов равна 360 градусов.
- Диагонали трапеции делят ее на два треугольника.
- Сумма длин двух противоположных сторон трапеции равна сумме длин двух оснований.
- Высота трапеции — это перпендикуляр, опущенный из одного основания к другому.
Примеры трапеций:
- Трапеция со сторонами 5 см, 8 см, 6 см и 6 см.
- Прямоугольная трапеция со сторонами 3 см, 4 см, 5 см и 5 см.
- Равнобедренная трапеция со сторонами 7 см, 5 см, 5 см и 3 см.
Что такое трапеция?
Чтобы определить трапецию, достаточно проверить параллельность двух сторон. Если они не параллельны, то фигура уже не будет являться трапецией.
Трапеции могут быть различных видов. Например, если оба боковых угла трапеции прямые, то такая фигура называется прямоугольной трапецией. Если все стороны трапеции равны, то такая фигура называется равнобокой трапецией. Также есть равнобедренные трапеции, у которых две боковые стороны равны, и трапеции с разносторонними основаниями.
Трапеции широко используются в геометрии и могут быть встречены в различных конструкциях и задачах. Знание свойств трапеции позволяет решать геометрические задачи и проводить различные доказательства.
Какие фигуры являются вырожденными трапециями?
Примеры вырожденных трапеций:
- Вырожденная прямоугольная трапеция: в такой фигуре все углы равны прямым углам, а боковые стороны параллельны друг другу. Следовательно, высота равна нулю.
- Вырожденная равнобедренная трапеция: в такой фигуре две боковые стороны равны друг другу, и углы при основании также равны друг другу. Такая трапеция также имеет высоту, равную нулю.
Таким образом, вырожденные трапеции представляют собой особый случай данной фигуры, когда она превращается в линию или отрезок.
Свойства трапеции
| Стороны | В трапеции две стороны параллельны, а две другие — не параллельны. |
| Углы | Трапеция имеет два прямых угла и два непрямых угла. |
| Диагонали | Диагонали трапеции пересекаются в точке, которая делит каждую из них на две равные части. |
| Площадь | Площадь трапеции можно вычислить по формуле: S = ((a + b) * h) / 2, где a и b — длины параллельных сторон, h — высота трапеции. |
| Периметр | Периметр трапеции можно вычислить по формуле: P = a + b + c + d, где a, b, c, d — длины сторон трапеции. |
Примеры трапеций включают: прямоугольник, параллелограмм, ромб, ромбоид и многоугольник.
Сумма углов трапеции
В трапеции можно выделить две пары углов: пару противоположных углов и пару смежных углов.
Сумма углов трапеции определяется следующим образом:
Сумма противоположных углов трапеции всегда равна 180 градусов. Это значит, что если один из противоположных углов равен 75 градусов, то второй противоположный угол будет равен 180 — 75 = 105 градусов.
Сумма смежных углов трапеции также равна 180 градусов. Например, если один смежный угол равен 60 градусов, то другой смежный угол будет равен 180 — 60 = 120 градусов.
Эти свойства суммы углов трапеции позволяют определить неизвестные углы и рассчитать геометрические параметры трапеции, такие как длина диагонали или площадь.
Основания и боковые стороны
Основание, образованное параллельными сторонами, называется нижним основанием, а другое основание — верхним основанием.
Боковые стороны трапеции — это непараллельные стороны, соединяющие основания.
Для трапеции существуют несколько свойств, связанных с основаниями и боковыми сторонами:
- Сумма углов при основаниях трапеции равна 180 градусам.
- Боковые стороны трапеции равны двум другим боковым сторонам.
- Сумма длин оснований трапеции равна сумме длин боковых сторон.
- Сумма длин двух противоположных боковых сторон трапеции равна разности длин оснований трапеции.
Например, рассмотрим трапецию ABCD, где AB — основание, данный край, CD — основание, данный вершине C, а BC и AD — боковые стороны. В этом случае, вышеупомянутые свойства будут выполняться для данной трапеции.
Равенство углов и сторон
По свойству равенства углов в трапеции противолежащие углы на каждом из оснований также равны между собой. Это означает, что угол ∠B равен углу ∠C, а угол ∠A равен углу ∠D.
Равенство углов и сторон позволяет проводить многочисленные геометрические выкладки и расчеты с трапецией, а также делает ее основой для решения различных задач и заданий по геометрии.
Примеры трапеций
| Прямоугольная трапеция | Неравнобедренная трапеция | Равнобедренная трапеция |
|---|---|---|
 |  |  |
| В прямоугольной трапеции две противоположные стороны перпендикулярны друг другу. | В неравнобедренной трапеции все четыре стороны имеют разные длины. | В равнобедренной трапеции две противоположные стороны равны друг другу. |
Трапеции широко используются в геометрии и применяются в различных областях, таких как строительство, архитектура и физика.
Вопрос-ответ:
Как определить трапецию?
Трапеция — это четырехугольник, у которого две стороны параллельны и две другие стороны не параллельны.
Какие свойства имеет трапеция?
У трапеции есть несколько свойств. Во-первых, сумма углов трапеции равна 360 градусов. Во-вторых, основания трапеции лежат на одной прямой.
Какие бывают виды трапеций?
В зависимости от величины углов и длины сторон, трапеции делят на прямоугольные и непрямоугольные. В прямоугольной трапеции угол между основанием и боковой стороной равен 90 градусам.
Можете привести примеры трапеций?
Конечно! Примеры трапеций могут быть следующими:
1) Трапеция с основаниями 6 и 10, и боковыми сторонами 4 и 4;
2) Прямоугольная трапеция с основаниями 8 и 12, и высотой 5.
Какие формулы используются для вычисления площади и периметра трапеции?
Формула для вычисления площади трапеции: S = ((a + b) * h) / 2, где a и b — основания трапеции, а h — высота. Формула для вычисления периметра: P = a + b + c + d, где a, b, c и d — длины сторон трапеции.