Смежные углы – это такие углы, которые имеют общую сторону и вершину. Они возникают, когда две прямые линии пересекаются. Знание смежных углов является важным элементом геометрии, особенно для учеников 7-го класса.
Чтобы определить смежные углы, нужно внимательно изучить конструкцию двух прямых линий и понять, какие углы можем считать смежными.
Сумма смежных углов всегда равна 180 градусов. Это означает, что если известна величина одного из смежных углов, то второй угол всегда можно вычислить, вычитая из 180 градусов известную величину угла.
Изучение смежных углов помогает детям развивать понимание пространственных отношений и абстрактное мышление. Это помогает им лучше понимать геометрические принципы и применять их в решении задач.
Теперь, когда вы знаете, что такое смежные углы и как вычислить их сумму, вы можете попрактиковаться в решении задач и применении этих знаний на практике.
Что такое смежные углы и где они применяются?
Сумма смежных углов всегда равна 180 градусам. Если мы знаем значение одного смежного угла, мы можем найти значение другого, используя эту теорему. Также мы можем использовать свойства смежных углов для доказательства различных геометрических теорем и решения геометрических задач.
Применение смежных углов
Смежные углы широко применяются в геометрии, а также в различных других областях. Некоторые из применений смежных углов:
- Геометрические построения и измерения
- Нахождение неизвестных углов для решения геометрических задач
- Доказательство геометрических теорем
- Визуализация и анализ фигур и моделей
- Проектирование и строительство зданий и сооружений
Понимание смежных углов и их свойств является важным навыком не только в геометрии, но и в других математических и научных областях. Оно поможет вам развить логическое мышление, улучшить способность решать задачи и находить решения в реальном мире.
Итак, смежные углы играют важную роль в геометрии и имеют практическое применение во многих областях. Изучение и понимание их свойств позволяет нам лучше разобраться в геометрических объектах, решить задачи и развить наши математические навыки.
Определение и примеры смежных углов
Сумма смежных углов всегда равна 180 градусов. Это свойство можно использовать для нахождения неизвестного угла, если известны другие смежные углы.
Примеры смежных углов:
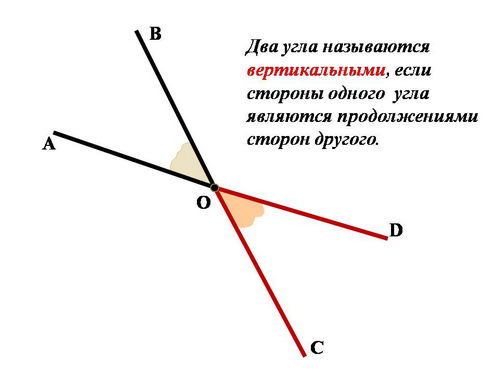
- Углы AOB и BOC являются смежными углами, так как они имеют общую сторону OB и общую вершину O.
- Углы EFD и GFD являются смежными углами, так как они имеют общую сторону FD и общую вершину F.
- Углы RST и TSR являются смежными углами, так как они имеют общую сторону ST и общую вершину S. Здесь угол RST является внутренним, а угол TSR — внешним смежным углом.
- Углы DEF и GEH являются смежными углами, так как они имеют общую сторону EH и общую вершину E. Здесь угол DEF является внутренним, а угол GEH — внешним смежным углом.
Знание о смежных углах помогает в решении геометрических задач, в том числе определении неизвестных углов и доказательстве свойств фигур.
Существуют ли ограничения для смежных углов?
Сумма смежных углов всегда равна 180 градусов. Это основное свойство смежных углов, которое можно использовать для решения задач по геометрии. Независимо от того, какие углы являются смежными, их сумма всегда будет равна 180 градусов.
Пример:
Пусть у нас есть два угла, A и B, которые являются смежными. Угол A равен 80 градусам. Тогда, используя свойство суммы смежных углов, мы можем найти меру угла B. Сумма угла A и угла B должна быть равна 180 градусов, поэтому:
| Угол A | Угол B |
|---|---|
| 80 градусов | 100 градусов |
Таким образом, угол B равен 100 градусам.
Из этого примера видно, что смежные углы могут иметь разные меры, но их сумма всегда будет равна 180 градусов. Это позволяет нам решать разнообразные задачи, связанные с углами и их свойствами в геометрии.
Формула для вычисления суммы смежных углов
В геометрии углы, делящие общую сторону и имеющие общую вершину, называются смежными углами. Сумма смежных углов зависит от их взаимного расположения и может быть вычислена с помощью специальной формулы. Формула для вычисления суммы смежных углов выглядит следующим образом:
Сумма смежных углов = 180°
Таким образом, если у нас есть два смежных угла, то их сумма всегда будет равна 180 градусам. Это свойство смежных углов позволяет упростить решение геометрических задач и вычислений, связанных с углами.
На практике формула для вычисления суммы смежных углов часто используется для нахождения значений углов, если известна сумма смежных углов или один из углов. Также она позволяет установить, являются ли данные углы смежными, если известны их значения.
Например, если у нас есть два смежных угла, один из которых равен 60 градусам, то второй угол будет равен:
Второй угол = 180° — 60° = 120°
Таким образом, сумма смежных углов в данном случае будет равна 180 градусам.
Пример вычисления суммы смежных углов
Пусть у нас есть два смежных угла: угол А и угол В. Угол А равен 80 градусов, а угол В равен 100 градусов. Чтобы найти сумму этих углов, нужно их просто сложить:
Сумма = угол А + угол В = 80 градусов + 100 градусов = 180 градусов
Таким образом, сумма смежных углов угол А и угол В равна 180 градусов.
Знание о смежных углах и их свойствах позволяет решать различные геометрические задачи, например, находить недостающие углы или углы в сложных фигурах.
Смежные углы в геометрии 7 класса
Сумма смежных углов всегда равна 180 градусам. Если углы являются смежными и дополнительными друг другу, то их сумма равна 90 градусам.
Смежные углы важны в геометрии, поскольку они помогают нам решать задачи, связанные с построением и измерением углов. Зная, что сумма смежных углов составляет определенное значение, мы можем вычислять неизвестные углы, находить дополнительные и суплементарные углы, а также проверять правильность построения фигур.
Прикладные задачи с смежными углами
Вот несколько прикладных задач, в которых сталкиваются с понятием смежных углов:
- Задача 1:
Дан параллелограмм ABCD, где AC и BD – диагонали. Найти меру угла ACD, если известно, что мера угла ABC равна 60 градусов. - Задача 2:
На плоскости даны две прямые l и m, пересекающиеся в точке O. Найти меру угла AOB, если прямая l образует с прямой m смежный угол, мера которого равна 120 градусам. - Задача 3:
Дан треугольник ABC. Биссектриса угла BAC пересекает сторону BC в точке D. Найти меру угла ABC, если мера смежного угла ABD равна 30 градусам. - Задача 4:
Дан прямоугольник PQRS. Оказалось, что мера угла SPQ равна 50 градусам. Найти меру смежного угла PQR.
Все эти задачи можно решить, используя свойства смежных углов. Например, если известно значение одного смежного угла, можно найти значение другого смежного угла, используя свойство их суммы, которая равна 180 градусов.
Решение данных задач позволяет применять знания о смежных углах на практике и понимать их значимость в геометрии.
Вопрос-ответ:
Какие углы называются смежными?
Смежные углы — это пара углов, которые имеют общую сторону и общую вершину.
Чему равна сумма смежных углов?
Сумма смежных углов всегда равна 180 градусов.
Какие особенности имеют смежные углы?
Смежные углы могут быть смежными дополнительными, смежными углами-сопряженными и смежными углами-вертикальными.
Можете привести примеры смежных углов?
Например, если у нас есть угол ABC и угол CBD, где вершина B общая, то эти углы являются смежными.
Какие свойства смежных углов важны с точки зрения геометрии в 7 классе?
Смежные углы суммируются до 180 градусов, что является важным свойством для решения геометрических задач в 7 классе.
Какие углы называются смежными?
Углы, у которых одна сторона и одна вершина общие, называются смежными углами.