Центральный угол – одно из важных понятий геометрии окружностей. Он определяется как угол между двумя лучами, исходящими из центра окружности и охватывающими дугу на этой окружности. Центральный угол неразрывно связан с окружностью, и его свойства играют важную роль в решении многих геометрических задач.
Один из основных результатов теории центральных углов гласит, что все такие углы, охватывающие одну и ту же дугу на окружности, равны между собой. Иными словами, если из центра окружности провести два луча, охватывающих одну и ту же дугу, то углы, образованные этими лучами с прямыми, проведенными из центра в любые точки дуги, будут равны. Это главное свойство центрального угла, которое широко применяется в геометрии.
Центральные углы также могут быть полными, полуполнми и строными, в зависимости от их величины. Полным называют тот центральный угол, который охватывает всю окружность – 360 градусов или 2π радиан. Полуполным называется центральный угол в 180 градусов или π радиан, так как он охватывает половину окружности.
Наличие свойств и формул, связанных с центральными углами, делает их мощным инструментом для решения геометрических задач на практике. Знание и понимание этих свойств позволяет конструировать и анализировать сложные фигуры, а также применять их в различных областях знания, таких как физика, астрономия и инженерия.
Определение центрального угла
Заметим, что угол может быть открытым или закрытым в зависимости от положения лучей. Открытым центральным углом называется тот, который может быть полностью помещен внутрь окружности, в то время как закрытым центральным углом называется тот, который дополняет окружность до полного круга.
Центральные углы имеют особые свойства. Например, все центральные углы, опирающиеся на дуги одинаковой длины, имеют одинаковую меру. Это свойство можно использовать для нахождения неизвестной меры центрального угла или дуги по известной мере другого центрального угла или дуги.
Окружность и центральный угол
Центральный угол — это угол, вершина которого совпадает с центром окружности, а стороны представляют собой лучи, соединяющие центр с двумя точками окружности.
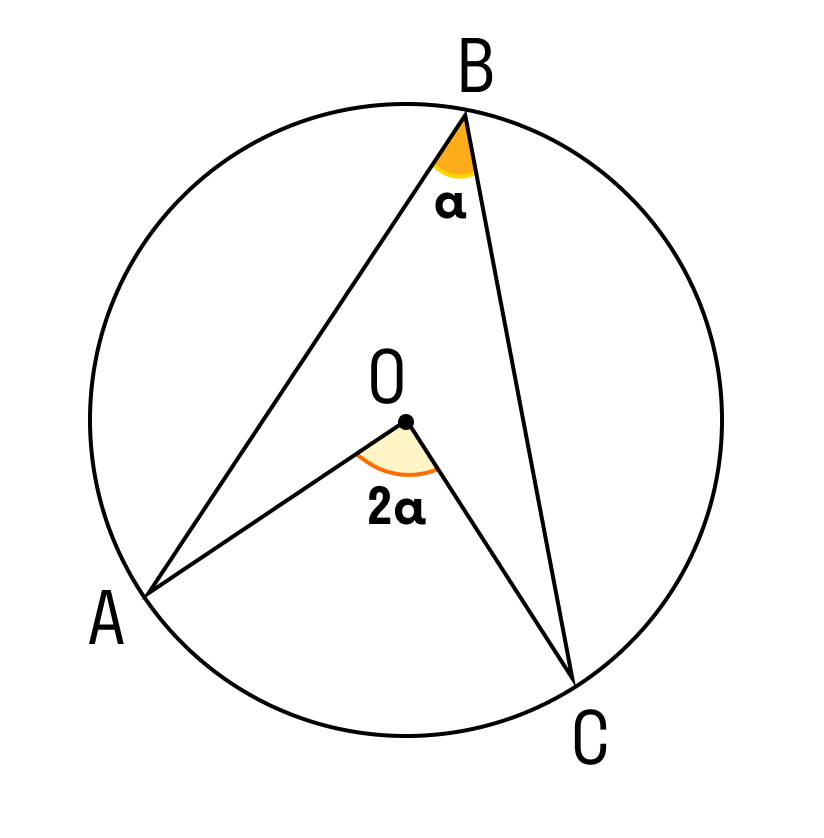
Один из основных результатов, касающихся окружности и центрального угла, — угол, опирающийся на дугу, в два раза больше любого другого угла, опирающегося на эту же дугу.
Свойства центральных углов:
| Свойство | Описание |
|---|---|
| 1. | Центральный угол имеет угол-объемлющую дугу, которая показывает, какая дуга сегмента находится внутри этого угла. |
| 2. | Центральные углы, опирающиеся на одну и ту же дугу, равны между собой. |
| 3. | Центральный угол, равный 180 градусов, называется прямым углом, а центральный угол, равный 360 градусов, называется полным углом. |
| 4. | Сумма всех центральных углов окружности равна 360 градусов. |
Центральные углы имеют важное значение в геометрии и находят применение в различных областях, таких как конструирование, архитектура и физика.
Арка и центральный угол
Арка — это часть окружности, ограниченная двумя точками на ее границе. Арка также может быть определена как угловая мера центрального угла. Длина арки измеряется в радианах или в градусах.
Свойства арки и центрального угла тесно связаны. Длина арки пропорциональна центральному углу: чем больше угол, тем больше арка. Кроме того, если центральный угол равен 360 градусам или 2π радиан, то арка будет равна длине окружности.
Арки и центральные углы также используются в геометрических вычислениях и решении задач на плоскости. Они помогают определить угловые отношения и применяются для измерения углов и расстояний.
Понимание арки и центрального угла является важным элементом в геометрии и при изучении свойств окружности. Они позволяют анализировать и понимать форму и взаимосвязь элементов окружности и помогают решать задачи, связанные с этими фигурами.
Измерение центрального угла
Для измерения центрального угла используется градусная мера. Полный оборот окружности составляет 360 градусов. Таким образом, центральный угол, равный 360 градусов, соответствует полному обороту окружности.
Другой единицей измерения центрального угла является радиан. Радиан – это длина дуги окружности, равная ее радиусу. Если длина дуги равна радиусу, то центральный угол, соответствующий этой дуге, равен 1 радиану.
Для перевода градусов в радианы и наоборот, используется следующее соотношение: 1 радиан = 180 / π градусов.
| Центральный угол | Градусы | Радианы |
|---|---|---|
| 1/2 оборота | 180° | π рад |
| 1/4 оборота | 90° | π/2 рад |
| 1/6 оборота | 60° | π/3 рад |
Таким образом, измерение центрального угла в градусах и радианах позволяет работать с окружностями и дугами, осуществлять их сравнение, вычислять соотношения между углами и дугами.
Свойства центрального угла
Свойства центрального угла:
1. Величина центрального угла равна длине дуги, на которую он опирается. То есть, если мы разделим окружность на n равных дуг, то величина каждого центрального угла будет равна 360°/n. Например, если окружность разделена на 4 равные дуги, то каждый центральный угол будет равен 360°/4 = 90°.
2. Центральные углы, опирающиеся на одну и ту же дугу, равны между собой. Независимо от положения центра и конечных точек лучей, если центральные углы опираются на одну и ту же дугу, то они равны. Это означает, что если два центральных угла опираются на дугу AB, то они имеют одинаковую величину.
3. Дополняющие центральные углы опираются на равные дуги. Если центральный угол AOB является дополнением центрального угла BOC, то это значит, что дуги AB и BC равны между собой. Величина каждой дуги равна половине суммы величин центральных углов.
4. Центральный угол, опирающийся на полную окружность, равен 360°. Если угол опирается на всю окружность, то он имеет величину в 360°, так как полная окружность составляет 360°.
Отношение длины дуги к углу
Отношение длины дуги окружности к ее центральному углу может быть определено с использованием формулы:
Длина дуги = (Угол/360) * 2 * π * Радиус
Здесь:
- Длина дуги — физическая длина части окружности, которая соответствует заданному центральному углу;
- Угол — мера центрального угла в градусах;
- π — математическая константа, приближенное значение которой 3,14159;
- Радиус — расстояние от центра окружности до ее точки.
Таким образом, отношение длины дуги к углу позволяет найти длину части окружности, которая соответствует заданному углу. Это свойство может быть использовано для решения различных задач в геометрии, физике и других областях науки.
Сумма центральных углов
Центральный угол окружности определяется как угол между двумя лучами, исходящими из центра окружности и соединяющими его с любой точкой на окружности.
Сумма центральных углов в любой окружности всегда равна 360 градусов. Это свойство является важным для решения различных задач и построения геометрических фигур.
Для вычисления суммы центральных углов в окружности можно использовать следующую формулу:
Сумма центральных углов = число углов * 360 градусов
Например, если в окружности имеется 6 центральных углов, то сумма этих углов будет равна:
Сумма центральных углов = 6 * 360 градусов = 2160 градусов
Это свойство позволяет быстро расчитать сумму центральных углов в окружности и использовать ее при решении различных геометрических задач.
Обратные центральные углы
Свойства обратных центральных углов:
- Обратные центральные углы, имеющие одну общую сторону и вершину, равны.
- Угол между касательной к окружности и хордой, делящей эту окружность на две равные части, будет иметь величину 90 градусов и будет обратным центральным углом.
- Сумма обратного центрального угла и центрального угла, делящего ту же дугу окружности, равна 180 градусов.
Изучение обратных центральных углов позволяет более глубоко понять свойства окружностей и их геометрическую структуру. Это важное понятие в геометрии и имеет широкое применение в различных задачах и заданиях.
Примеры применения центрального угла
1. Красное сияние
Центральный угол может использоваться для описания эффекта красного сияния, который наблюдается при закате солнца или восходе луны. В данном случае, точка, вокруг которой совершается движение светила, является центральным углом, а линия, соединяющая точку наблюдения с светилом, представляет собой сторону угла. Угол, который охватывается наблюдателем, будет являться центральным углом и определяет величину красного сияния.
2. Навигация
Центральные углы используются в навигации для определения направления и расстояния между двумя точками на земной поверхности. Например, моряки используют центральные углы для определения азимута, то есть угла между направлением на север и прямым направлением на цель. Это позволяет суднам и пилотам точно указывать на карте направление движения.
3. Геодезия
В геодезии центральные углы используются для измерения угловых отклонений между точками на земной поверхности. Например, при создании триангуляционной сети, где измеряются углы между тремя точками, центральные углы позволяют определить географические координаты каждой точки. Это является основой для составления карт и определения границ между землевладениями.
4. Архитектура
Центральные углы применяются при проектировании и строительстве зданий и сооружений. Например, архитекторы используют центральные углы для определения расположения и выравнивания стен, окон, дверей и других элементов. Это позволяет создавать гармоничные и симметричные конструкции, где каждый элемент занимает определенное положение по отношению к центральному углу.
Таким образом, центральные углы широко применяются в различных областях, таких как астрономия, навигация, геодезия и архитектура, где они помогают определить направление, расстояние и положение объектов в пространстве.
Вопрос-ответ:
Что такое центральный угол окружности?
Центральный угол окружности — это угол, вершина которого находится в центре окружности, а стороны проходят через две точки на этой окружности.
Как определить меру центрального угла?
Мера центрального угла равна длине дуги, заключенной между его сторонами, измеренной в радианах или градусах.
Какие свойства имеют центральные углы?
У центрального угла окружности есть несколько свойств: его мера равна длине дуги, проведенной между его сторонами; центральные углы, имеющие равные меры, равны между собой; сумма мер всех центральных углов в окружности равна 360 градусов или 2π радиан.
В чем разница между центральным углом и вписанным углом?
Центральный угол определяется двумя точками на окружности и проходит через центр окружности, в то время как вписанный угол определяется двумя точками на окружности и проходит через касательные, опираясь на одну сторону на дугу, а на другую — на хорду.
Какие примеры применения центральных углов в реальной жизни?
Центральные углы используются в различных областях, включая геометрию, физику, графику и архитектуру. Например, они помогают визуально представить расстояние и направление воздушных или морских путей, определить углы в геодезии и исследовать форму окружности в математических моделях.
Что такое центральный угол окружности?
Центральный угол окружности — это угол с вершиной в центре окружности и сторонами, которыми являются две линии, идущие из центра к любым точкам окружности.
Какова сумма центральных углов окружности?
Сумма всех центральных углов окружности равна 360 градусов.