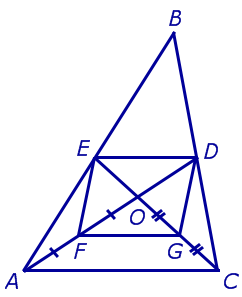
Медиана треугольника — это особый отрезок, который соединяет вершину треугольника с серединой противоположной стороны. Изучение медиан треугольника в геометрии является важным аспектом, поскольку они обладают рядом уникальных свойств и играют значительную роль в анализе и решении задач, связанных с треугольниками.
Медианы могут быть различными: каждая из них соединяет одну вершину с серединой противоположной стороны. В треугольнике всегда присутствуют три медианы, и они пересекаются в одной точке, называемой центром медиан.
Одним из основных свойств медиан является то, что они делят другие медианы и стороны треугольника в соотношении 2:1. Иными словами, длина каждой медианы равна сумме длин двух других медиан, поделенной на 2. Кроме того, точка пересечения медиан равноудалена от вершин треугольника, что делает ее центром тяжести или барицентром треугольника.
Определение медианы треугольника
Каждый треугольник имеет три медианы, которые пересекаются в одной точке, называемой центром медиан треугольника или центром тяжести. Эта точка делит каждую медиану в отношении 2:1, то есть расстояние от вершины до центра медианы в два раза больше, чем от центра медианы до середины противоположной стороны.
Медиана треугольника имеет несколько важных свойств:
| 1. | Медиана делит треугольник на две равные части по площади. |
| 2. | Центр масс (центр тяжести) треугольника совпадает с центром пересечения медиан. Это значит, что если треугольник представлен вещественной плоскостью с одинаковой плотностью материала, то он будет находиться в равновесии. |
| 3. | Прямая, содержащая медиану, делит площадь треугольника на две равные части. |
| 4. | Длина медианы может быть вычислена с использованием формулы: ma = √(2b² + 2c² — a²) / 2, где ma — длина медианы, a, b, c — длины сторон треугольника. |
Медианы треугольника могут быть использованы в различных математических и геометрических задачах, а также имеют практическое применение в строительстве и дизайне.
Что такое медиана треугольника?
Медиана треугольника проходит через вершину и середину противоположной стороны, и делит данную сторону на две равные части. Таким образом, каждая медиана делит треугольник на два равных по площади треугольника.
Медианы треугольника пересекаются в одной точке, называемой центром масс треугольника или точкой пересечения медиан. Координаты центра масс могут быть определены как среднее арифметическое координат вершин треугольника.
Медианы треугольника обладают некоторыми интересными свойствами. Например, каждая медиана равна половине суммы длин противоположной стороны и смежных сторон.
Также, медиана делит площадь треугольника на две равные части. Это означает, что если мы изучаем геометрические фигуры на основе треугольника, то при разделении на части мы можем использовать медианы для равномерного разделения площади.
| Свойства медиан треугольника: |
|---|
| Каждая медиана делит треугольник на два равных по площади треугольника. |
| Каждая медиана равна половине суммы длин противоположной стороны и смежных сторон. |
| Медианы пересекаются в одной точке — центре масс треугольника. |
| Центр масс может быть определен как среднее арифметическое координат вершин треугольника. |
Как определить медиану треугольника?
- Выберите любую сторону треугольника.
- На найденной стороне отложите отметку в середине и соедините эту отметку с противоположным углом треугольника.
- Таким образом, получается медиана треугольника, которая проходит через середину стороны и точку пересечения с противоположным углом.
Важно отметить, что каждая сторона треугольника имеет свою медиану. Треугольник может иметь три медианы, и все они пересекаются в одной точке, называемой центром масс треугольника или точкой пересечения медиан.
Медианы треугольника обладают следующими свойствами:
- Медиана делит сторону треугольника на две равные части.
- Медиана равна половине длины соответствующей стороны треугольника.
- Медиана перпендикулярна соответствующей стороне треугольника.
- Точка пересечения медиан является центром масс треугольника.
Медианы треугольника играют важную роль в геометрии и находят применение в различных задачах, включая определение центра масс треугольника или нахождение точки пересечения медиан в других фигурах.
Свойства медианы треугольника
Свойство 1: Середина
Медиана всегда проходит через середину стороны треугольника. Это означает, что если мы разделим медиану пополам, то получим два отрезка равной длины.
Свойство 2: Пересечение
Медианы треугольника пересекаются в одной точке, которая называется центром тяжести или барицентром треугольника. Эта точка делит каждую медиану в отношении 2:1.
Свойство 3: Отношение площадей
Площадь треугольника, образованного медианой, равна 3/4 площади исходного треугольника. Это значит, что треугольник, образованный медианами, имеет ту же форму, но меньшую площадь.
Свойство 4: Устойчивость
Медиана треугольника остается медианой даже при изменении размеров треугольника. Это значит, что если мы увеличим или уменьшим треугольник, медиана все равно будет проходить через середину стороны и пересекаться с другими медианами в одной точке.
Использование медиан треугольника позволяет находить различные геометрические свойства и решать задачи в различных областях, таких как строительство, архитектура, физика и многое другое.
Медиана треугольника делит его на две равные части
Основное свойство медианы заключается в том, что она делит противолежащую сторону пополам, то есть делит треугольник на два равных треугольника. Данное свойство можно применить для решения различных задач и построения дополнительных линий в треугольнике.
Кроме того, медианы треугольника пересекаются в точке, которая называется центром медиан треугольника или центроидом. Центроид является точкой пересечения всех трех медиан треугольника и является центром тяжести треугольника. В этой точке сумма расстояний до вершин треугольника минимальна.
Таким образом, медиана треугольника не только делит его на две равные части, но и играет важную роль в определении центра тяжести треугольника. Это свойство медианы выполняется для любого треугольника, независимо от его формы и размеров.
Медиана треугольника пересекается в точке, в которой сходятся все медианы
Центр масс треугольника является точкой пересечения всех медиан и обладает следующими свойствами:
- Медианы треугольника делятся центром масс на три равные части.
- Расстояние от центра масс до каждой из вершин треугольника равно двум третям длины медианы, и они образуют отрезки, известные как высоты треугольника.
- Центр масс треугольника относится к каждой из сторон треугольника как соотношение 1:2. Это означает, что длина отрезка, соединяющего центр масс с вершиной, в два раза больше, чем длина отрезка, соединяющего центр масс с серединой противоположной стороны.
- Если медиана треугольника продолжена за вершину, то ее продолжение будет делить противоположную сторону на две равные части.
Таким образом, центр масс треугольника, точка пересечения всех медиан, является важным геометрическим свойством треугольника. Он имеет много приложений в физике, инженерии и других областях науки, где треугольники широко используются для моделирования и анализа систем.
Применение медианы треугольника в геометрии
Центроид является точкой пересечения трех медиан и обладает следующими интересными свойствами:
| Свойство | Описание |
|---|---|
| 1 | Центр тяжести треугольника делит каждую медиану в отношении 2:1 |
| 2 | Центр тяжести является центром тяжести для массы треугольника |
| 3 | Медианы треугольника делят его на шесть равных треугольников |
| 4 | Центроид является точкой симметрии для треугольника |
Применение медиан треугольника в геометрии может быть разнообразным. Одним из простых примеров является определение центра тяжести для неоднородного двухмерного объекта. Для этого объекта можно представить себе как треугольник, соединив его три точки с помощью медиан, и найти центроид треугольника.
Кроме того, медианы треугольника могут быть полезны при решении различных задач геометрии, таких как вычисление площади треугольника, построение определенных прямых или точек треугольника, и т.д. Медианы также используются в теории треугольников и могут быть применены для доказательства различных геометрических теорем.
Таким образом, понимание свойств и применение медианы треугольника в геометрии позволяет решать различные задачи, связанные с треугольниками, и облегчает изучение и понимание геометрии в целом.
Как использовать медиану треугольника для нахождения площади?
Как оказывается, медиана треугольника может быть полезной для нахождения площади треугольника, особенно когда известны длины этих медиан.
Для использования медианы треугольника для нахождения площади, следуйте следующим шагам:
- Найдите длины трех медиан треугольника.
- Умножьте длину каждой медианы на 2.
- Найдите сумму полученных значений.
- Извлеките квадратный корень из полученной суммы.
- Умножьте полученное значение на 3.
Полученное значение будет являться площадью треугольника, если известны длины трех медиан.
Таким образом, медианы треугольника позволяют нам найти площадь треугольника, используя только длины медиан, без необходимости знать длины сторон треугольника. Это может быть полезным, особенно если стороны треугольника трудно измерить или найти.
Вопрос-ответ:
Что такое медиана треугольника и как ее определить?
Медиана треугольника — это отрезок, соединяющий одну вершину треугольника с серединой противоположной стороны. Определить медиану можно следующим образом: берем одну из вершин треугольника и соединяем ее с серединой противоположной стороны.
Есть ли у медиан треугольника какие-то свойства?
Да, у медиан треугольника есть несколько свойств. Одно из них состоит в том, что медианы треугольника пересекаются в одной точке, которая называется точкой пересечения медиан и является центром тяжести треугольника.
Можно ли доказать, что медиана равна половине соответствующей стороны?
Да, можно доказать, что медиана равна половине соответствующей стороны треугольника. Для этого достаточно воспользоваться свойством схожести треугольников и применить соответствующие теоремы.
Зачем нужны медианы треугольника?
Медианы треугольника играют важную роль в геометрии и имеют различные применения. Они могут использоваться для определения центра тяжести треугольника, построения вписанной окружности или для нахождения площади треугольника.
Какие еще свойства есть у медиан треугольника?
Помимо того, что медианы треугольника пересекаются в одной точке и равны половине соответствующей стороны, они также делят треугольник на шесть равных треугольников и сами являются биссектрисами этих треугольников.
Что такое медиана треугольника?
Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Какие свойства имеет медиана треугольника?
Медианы треугольника делятся одной точкой, называемой центром тяжести, которая располагается внутри треугольника. Также медианы делят треугольник на шесть равных треугольников.