Многоугольник — это фигура, состоящая из прямых отрезков (сторон), которые соединяют вершины. Каждая вершина многоугольника является концом двух соседних сторон. В зависимости от количества вершин многоугольник может быть треугольником (3 вершины), четырехугольником (4 вершины), пятиугольником (5 вершин) и так далее. Одним из интересных видов многоугольника является многоугольник вписанный в окружность.
Многоугольник считается вписанным в окружность, если все его вершины лежат на окружности. В центре окружности находится точка, из которой проведены радиусы к вершинам многоугольника. Радиусы являются линиями, соединяющими центр окружности с вершинами многоугольника.
Многоугольник вписанный в окружность обладает рядом интересных свойств:
— Сумма всех углов многоугольника равна 360 градусам.
— Все радиусы, проведенные к вершинам многоугольника, равны по длине.
— Противоположные углы многоугольника суммируются до 180 градусов.
— Сумма произвольных двух смежных углов многоугольника также равна 180 градусам.
— Периметр многоугольника вписанного в окружность зависит только от длины радиуса окружности.
Многоугольники вписанные в окружность широко применяются в различных областях, включая геометрию, физику, строительство и дизайн. Изучение их свойств позволяет получить более глубокое понимание геометрии и решать сложные задачи вида «Вписать многоугольник в окружность». Кроме того, такие многоугольники являются красивыми и симметричными фигурами, привлекающими внимание и вызывающими эстетическое удовлетворение.
Определение многоугольника вписанного в окружность
Для того чтобы многоугольник был вписанным в окружность, должны выполняться следующие условия:
- Все вершины многоугольника лежат на окружности.
- У каждой стороны многоугольника есть общая точка (центр окружности).
Многоугольник, вписанный в окружность, обладает рядом свойств:
- Сумма всех внутренних углов многоугольника равна (n-2)·180°, где n — количество вершин многоугольника. Для треугольника сумма углов составляет 180°, для четырехугольника — 360° и так далее.
- Центр окружности совпадает с центральной точкой многоугольника, которая является точкой пересечения всех его диагоналей.
- Радиус окружности, вписанной в многоугольник, может быть вычислен по формуле: r = a / (2 * sin(180° / n)), где r — радиус окружности, a — длина одной стороны многоугольника, n — количество вершин многоугольника.
Многоугольник, вписанный в окружность, обладает рядом интересных геометрических и алгебраических свойств, которые широко применяются в геометрии и математике.
Многоугольник
В зависимости от количества вершин многоугольники могут быть классифицированы:
- Треугольник — многоугольник, состоящий из трех вершин и трех сторон.
- Четырехугольник — многоугольник, состоящий из четырех вершин и четырех сторон.
- Пятиугольник — многоугольник, состоящий из пяти вершин и пяти сторон.
- И так далее, с шестиугольниками, семиугольниками и т.д.
Если все стороны и углы многоугольника равны, то он называется правильным многоугольником.
Многоугольник может быть выпуклым или невыпуклым:
- Выпуклый многоугольник — все внутренние углы меньше 180 градусов.
- Невыпуклый многоугольник — имеет внутренние углы больше 180 градусов.
Многоугольники широко используются в геометрии и различных областях науки и техники. Их свойства и закономерности изучаются в математическом анализе и теории чисел.
Вписанный многоугольник
У вписанных многоугольников есть несколько интересных свойств. Одно из них — равенство центральных углов и соответствующих им углов вписанного многоугольника. Если провести хорды от центра окружности к вершинам многоугольника, то эти хорды разделят многоугольник на равные углы.
Еще одно свойство вписанных многоугольников связано с длинами сторон и радиусом окружности. Сумма длин любых двух сторон вписанного многоугольника больше или равна диаметру окружности, а разность длин сторон меньше или равна диаметру окружности.
Область, ограниченная вписанным многоугольником и окружностью, называется окружностью Эйлера. Эта область имеет своеобразную геометрическую красоту и широко используется в архитектуре и дизайне.
Изучение вписанных многоугольников помогает лучше понять геометрию и ее применение в различных областях знаний. Они также играют важную роль в теории игр и комбинаторике, где многоугольники используются для моделирования различных задач и оптимизации решений.
Окружность
Окружность может быть определена как геометрическое место точек, которые находятся на одинаковом расстоянии от центра. В математической нотации окружность обозначается символом O и иногда дополнительно указывается её центр и радиус, например, O(A, r), где A — центр окружности, а r — радиус.
Окружность имеет несколько основных свойств:
| Свойство | Описание |
|---|---|
| Диаметр | Диаметр окружности равен удвоенному значению её радиуса, то есть d = 2r. |
| Длина окружности | Длина окружности можно выразить через её радиус или диаметр, используя формулу L = 2πr или L = πd, где π (пи) – математическая константа, примерно равная 3,14159. |
| Площадь окружности | Площадь окружности можно выразить через её радиус или диаметр, используя формулу S = πr^2 или S = (π/4)d^2. |
Окружность часто используется в геометрии для решения задач, связанных с построением геометрических фигур, нахождением периметра и площади, а также для изучения свойств многоугольников вписанных в окружность.
Свойства многоугольника вписанного в окружность
Многоугольник, вписанный в окружность, обладает рядом интересных свойств:
- Все стороны многоугольника являются радиусами окружности.
- Все углы многоугольника, образованные сторонами и хордами, равны между собой.
- Сумма всех внутренних углов многоугольника всегда равна (n-2) * 180 градусов, где n — количество сторон многоугольника.
- Радиус окружности, вписанной в многоугольник, можно выразить через его площадь S и полупериметр p по формуле: r = 2S/p, где r — радиус окружности.
- Многоугольник, вписанный в окружность, всегда является выпуклым многоугольником.
Использование этих свойств позволяет решать различные задачи из геометрии, связанные с вписанными многоугольниками. Например, можно найти радиус вписанной окружности, если известны площадь и периметр многоугольника.
Соотношения между углами многоугольника
Многоугольник вписанный в окружность обладает рядом интересных свойств, в том числе и особые соотношения между его углами.
Первое особенное соотношение состоит в том, что сумма всех внутренних углов вписанного многоугольника равна 180° × (n-2), где n — количество сторон многоугольника. Например, для треугольника (n=3) сумма углов будет равна 180°, а для пятиугольника (n=5) сумма углов будет равна 540°.
Второе соотношение связано с центральным углом многоугольника. Центральный угол многоугольника равен 360° ÷ n, где n — количество сторон многоугольника. Например, для треугольника (n=3) центральный угол будет равен 120°, а для пятиугольника (n=5) центральный угол будет равен 72°.
Также вписанный многоугольник обладает равенством между внутренним и центральным углами, если они соответствуют одной и той же дуге окружности. То есть, если угол многоугольника равен α, а центральный угол равен β, то α = β, если и только если они оба соответствуют одной и той же дуге окружности.
Знание этих соотношений позволяет нам более глубоко изучать особенности и свойства многоугольников вписанных в окружность.
Соотношения между сторонами многоугольника
Многоугольник, вписанный в окружность, обладает рядом интересных свойств, включая пропорциональные соотношения между его сторонами.
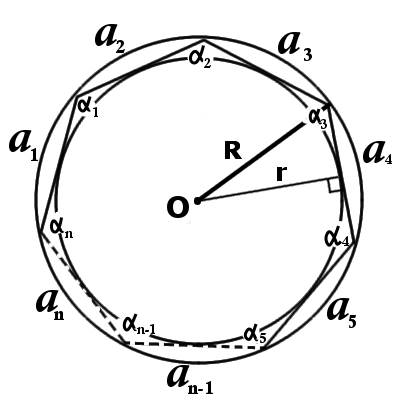
Пусть у нас есть многоугольник с n сторонами, вписанный в окружность радиусом R. Пусть a1, a2, …, an — длины его сторон. Тогда справедливы следующие формулы:
Соотношение между сторонами:
a1 : a2 : … : an = 1 : sin(α1) : … : sin(αn) = 2R : 2R : … : 2R = R : R : … : R
где α1, α2, …, αn — соответствующие центральные углы многоугольника.
Это означает, что длины сторон многоугольника пропорциональны соответствующим синусам центральных углов и радиусу окружности.
Таким образом, если мы знаем длину одной из сторон и радиус окружности, мы можем найти длины остальных сторон многоугольника, используя пропорциональные соотношения.
Центральный угол многоугольника вписанного в окружность
Центральным углом многоугольника вписанного в окружность называется угол, вершина которого совпадает с центром окружности, а стороны проходят через соседние вершины многоугольника.
Свойства центрального угла многоугольника вписанного в окружность:
- Мера центрального угла равна удвоенной мере соответствующего угла многоугольника на окружности.
- Теорема: сумма мер всех центральных углов многоугольника вписанного в окружность равна 360 градусов.
Центральные углы многоугольника вписанного в окружность играют важную роль при изучении свойств фигур с окружностями. Они позволяют установить соотношения между углами и сторонами многоугольника и окружности.
Центральные углы также помогают определить свойства многоугольника вписанного в окружность, такие как длины дуг и центры окружностей, описанных вокруг многоугольника. Кроме того, центральные углы позволяют установить связь между многоугольниками вписанными в одну и ту же окружность.
Вопрос-ответ:
Что такое многоугольник, вписанный в окружность?
Многоугольник, вписанный в окружность, — это многоугольник, вершины которого лежат на окружности.
Как найти углы в многоугольнике, вписанном в окружность?
Для нахождения углов в многоугольнике, вписанном в окружность, можно использовать формулу: угол равен 360°, деленный на количество сторон многоугольника.
Какое свойство имеют диагонали в многоугольнике, вписанном в окружность?
Диагонали в многоугольнике, вписанном в окружность, являются радиусами окружности или их продолжениями.
Как найти площадь многоугольника, вписанного в окружность?
Чтобы найти площадь многоугольника, вписанного в окружность, нужно разделить его на треугольники, с вершинами в центре окружности и на его сторонах, а затем сложить площади всех полученных треугольников.