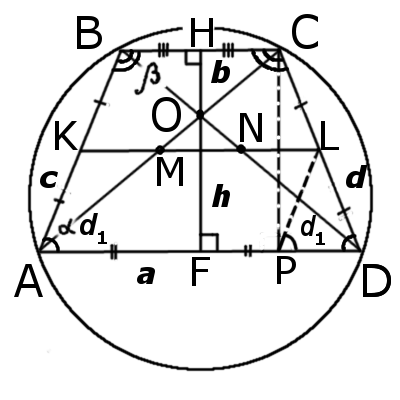
Трапеция – это четырехугольник, у которого две стороны параллельны и неравны, а две другие стороны – непараллельны и равны. Существует несколько типов трапеций, и одним из наиболее интересных из них является равнобедренная трапеция.
Равнобедренная трапеция – это такая трапеция, у которой основания (боковые стороны) имеют одинаковую длину, а высота (расстояние между основаниями) перпендикулярна им и делит их на две равные части. Этот тип трапеции обладает несколькими интересными свойствами.
Свойство 1: Диагонали равнобедренной трапеции равны между собой. Это значит, что отрезок, соединяющий вершины трапеции, является биссектрисой угла между основаниями и делит его на два равных угла.
Свойство 2: Высота равнобедренной трапеции является средней линией треугольника, образованного диагоналями. Это означает, что длина высоты равна половине суммы длин диагоналей.
Свойство 3: Равнобедренная трапеция может быть вписана в окружность. Для этого достаточно, чтобы сумма двух противоположных углов была равна 180 градусов. Вписанная в окружность трапеция обладает рядом интересных геометрических свойств, а также имеет больше степеней свободы в действиях с геометрическими фигурами.
Определение равнобедренной трапеции
Основные свойства равнобедренной трапеции:
| 1. | Углы при основании равны между собой. |
| 2. | Диагонали равны. |
| 3. | Боковые стороны равны между собой. |
| 4. | Сумма углов при основании равна 180 градусам. |
Эти свойства позволяют легко определить равнобедренную трапецию и использовать их при решении задач, связанных с данным видом фигур.
Что такое равнобедренная трапеция
У равнобедренной трапеции есть несколько свойств:
- Основания равнобедренной трапеции параллельны друг другу.
- Диагонали равнобедренной трапеции равны друг другу и перпендикулярны основанию.
- Сумма углов при основании равнобедренной трапеции равна 180 градусам, а два противоположных угла совпадают по величине.
- Высота, опущенная из вершины равнобедренной трапеции на основание, является медианой и биссектрисой этой трапеции.
Равнобедренные трапеции являются особенными и широко используются в геометрии и в различных приложениях, например при решении задач на нахождение площади фигур или в построении разнообразных конструкций.
Свойства равнобедренной трапеции
1. Равные основания: Равнобедренная трапеция имеет два основания, которые являются равными по длине. Основания — это пара параллельных сторон трапеции.
2. Равные боковые стороны: Равнобедренная трапеция имеет две боковые стороны, которые также равны по длине. Эти стороны соединяют основания трапеции и образуют ее боковые грани.
3. Равные углы: В равнобедренной трапеции два угла, образованные основаниями и боковыми сторонами, также равны между собой. Это свойство называется свойством равности углов в равнобедренной трапеции.
4. Высота: Высотой равнобедренной трапеции называется отрезок, соединяющий основания трапеции и перпендикулярный им. Высота является осью симметрии для равнобедренной трапеции и делит ее на два равных треугольника.
Знание этих свойств позволяет упростить решение задач, связанных с равнобедренными трапециями, и помогает лучше понимать их структуру и особенности.
Углы равнобедренной трапеции
У равнобедренной трапеции два угла на основании равны друг другу. Эти углы называются основными или равными. Они расположены у основания трапеции и образуются в точках пересечения основания с наклонными сторонами.
Также в равнобедренной трапеции существуют два равных угла между наклонными сторонами и боковыми сторонами. Эти углы называются боковыми или вертикальными. Они расположены противоположно друг другу и образуются при пересечении наклонных сторон.
| Основные углы | Боковые углы | |
|---|---|---|
| Расположение | У основания трапеции | Между наклонными и боковыми сторонами |
| Свойство | Равны друг другу | Равны между собой |
Зная эти свойства углов, можно легко обнаружить равнобедренную трапецию и использовать их для доказательства различных теорем и задач о равнобедренных трапециях.
Диагонали равнобедренной трапеции
Основные свойства диагоналей равнобедренной трапеции:
- Диагонали равны между собой. Обозначим диагонали как AC и BD, где AC — основа трапеции, а BD — диагональ. Таким образом, AC=BD.
- Они делят друг друга пополам. То есть точка их пересечения, обозначим ее как O, является серединой каждой диагонали. То есть AO=CO=DO=BO.
- Диагонали являются биссектрисами углов, образованных основой трапеции и боковыми сторонами. То есть угол ADC = угол BCD и угол ABD = угол ACD.
Диагонали равнобедренной трапеции имеют важное значение при решении различных задач, а также позволяют вычислять другие характеристики этой фигуры, например, площадь.
Примеры равнобедренных трапеций
Пример 1:
Рассмотрим трапецию ABCD, где AB и CD — основания, а AD и BC — боковые стороны. Если длины боковых сторон AD и BC равны, то трапеция ABCD является равнобедренной. В этом случае углы при вершинах A и B также будут равными, а углы при вершинах C и D будут равными. Таким образом, трапеция ABCD будет иметь две равные стороны и два равных угла.
Пример 2:
Рассмотрим трапецию PQRS, где PQ и RS — основания, а PS и QR — боковые стороны. Если длины боковых сторон PS и QR равны, то трапеция PQRS является равнобедренной. В этом случае углы при вершинах P и Q также будут равными, а углы при вершинах R и S будут равными. Таким образом, трапеция PQRS будет иметь две равные стороны и два равных угла.
Пример 3:
Рассмотрим трапецию LMNO, где LM и NO — основания, а LO и MN — боковые стороны. Если длины боковых сторон LO и MN равны, то трапеция LMNO является равнобедренной. В этом случае углы при вершинах L и M также будут равными, а углы при вершинах N и O будут равными. Таким образом, трапеция LMNO будет иметь две равные стороны и два равных угла.
Важно отметить, что для равнобедренной трапеции необязательно, чтобы длины оснований были равными. Достаточно, чтобы длины боковых сторон были равными.
Вопрос-ответ:
Что такое равнобедренная трапеция?
Равнобедренная трапеция — это четырехугольник, у которого две пары сторон равны.
Какие свойства у равнобедренной трапеции?
У равнобедренной трапеции две пары оснований равны, а две боковые стороны равны между собой.
Как можно определить, является ли трапеция равнобедренной?
Трапеция является равнобедренной, если равны одна из пар баз и две боковые стороны.
Как найти площадь равнобедренной трапеции?
Площадь равнобедренной трапеции можно найти, умножив половину суммы длин оснований на высоту.
Если в трапеции все стороны равны, является ли она равнобедренной?
Да, если в трапеции все стороны равны, то она является равнобедренной.
Что такое равнобедренная трапеция?
Равнобедренная трапеция — это четырехугольник, у которого две стороны параллельны и равны, а две другие стороны неравны.
Какие свойства имеет равнобедренная трапеция?
У равнобедренной трапеции есть несколько свойств. Она имеет две параллельные равные стороны и две неравные стороны. Также, у всех ее углов сумма равна 180 градусов.