
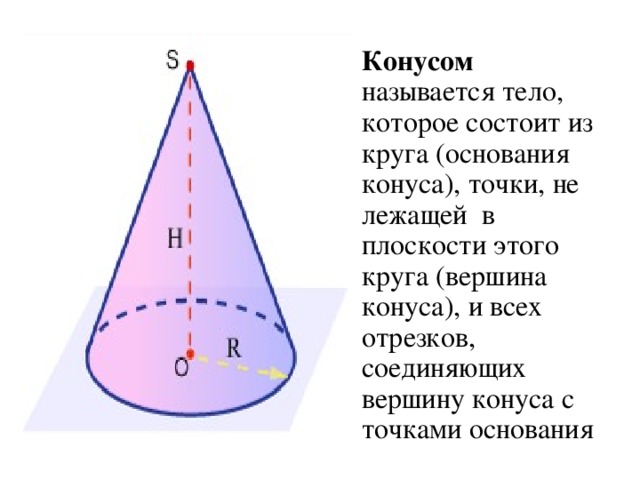
Конус — это одна из основных геометрических фигур в трехмерном пространстве. Он относится к классу многогранников и имеет некоторые особенности, которые делают его уникальным и легко узнаваемым.
Конус состоит из двух основных элементов — основы и боковой поверхности. Основа представляет собой плоскую фигуру, обычно круг или эллипс, а боковая поверхность — это поверхность, образованная линиями, соединяющими каждую точку основы с вершиной конуса.
Один из ключевых параметров конуса — его высота, определяющая расстояние от основы до вершины. Высота конуса соотносится с радиусом основы и определяет его форму и размеры.
Видимо создал
Основания конуса
Основания конуса — это две плоскости, которые являются кругами и лежат на противоположных концах конуса. Основание конуса имеет форму круга и обычно обозначается как S. Основания конуса могут быть разных размеров и форм, но всегда лежат в одной плоскости.
Боковая поверхность конуса
Боковая поверхность конуса — это выпуклая поверхность, которая соединяет два основания конуса. Эта поверхность формируется из бесконечного числа секущих плоскостей, и каждая секущая поверхность образует ребра конуса. Боковая поверхность конуса можно представить как оболочку, образуемую линией, которая соединяет все точки оснований конуса.
Таким образом, конус — это геометрическое тело, состоящее из двух оснований и боковой поверхности, которая их соединяет. Конусы встречаются в различных областях нашей жизни, от архитектуры до естественных образований. Их форма и свойства делают их интересными для изучения и применения в разных областях науки и техники.
Строение конуса
Основание
Основание конуса – это плоская фигура, которая ограничивает его нижнюю часть. Основание может быть различной формы, например, круг, эллипс, треугольник или многоугольник. Форма основания определяет форму и свойства конуса.
Боковая поверхность
Боковая поверхность конуса состоит из всех отрезков, соединяющих вершину конуса с точками основания. Все эти отрезки образуют плоскость, которая наклонена относительно основания. Боковая поверхность конуса может быть кривой или плоской, а ее форма зависит от формы и размеров основания.
Боковая поверхность конуса является образующей, а ее длина равна длине окружности основания, умноженной на высоту конуса и деленной на периметр основания.
Строение конуса позволяет ему иметь уникальные свойства и применения в различных областях, таких как архитектура, строительство, геодезия и даже в кулинарии.
Типы конусов
Прямой конус
Прямой конус — это конус, у которого основание неперпендикулярно оси, а также все генератриксы пересекают ось в одной точке.
Наклонный конус
Наклонный конус — это конус, у которого основание неперпендикулярно оси и все генератриксы не пересекают ось, а располагаются в плоскости, параллельной оси.
В таблице ниже представлены основные различия между прямым и наклонным конусами:
| Тип конуса | Форма основания | Положение осей |
|---|---|---|
| Прямой конус | Круг | Ось перпендикулярна основанию |
| Наклонный конус | Эллипс | Ось наклонена относительно основания |
Таким образом, различные типы конусов отличаются формой и положением основания, а также направлением генератриксов.
Расчет объема конуса
Формула для расчета объема конуса:
V = (1/3) * π * r2 * h
Где:
- V — объем конуса.
- π — математическая константа, примерно равная 3.14159.
- r — радиус основы конуса.
- h — высота конуса.
Для расчета объема конуса необходимо знать значения его радиуса и высоты. Подставив их в формулу, можно получить точное значение объема конуса.
Геометрические свойства конуса
Конус обладает рядом геометрических свойств, которые делают его особенным и применимым в различных областях.
Плоские сечения
Если плоскость пересекает конус, проходя через его вершину и параллельна основанию, то в результате получится подобие фигуры основания. Если плоскость пересекает конус, проходя через его вершину и не параллельна основанию, то в результате получится так называемое сечение конуса. В зависимости от угла, под которым плоскость пересекает конус, сечение может представлять собой эллипс, гиперболу, параболу или отрезок.
Объем и поверхность конуса
Объем конуса вычисляется по формуле V = (1/3)πr^2h, где r — радиус основания, а h — высота конуса. Поверхность конуса состоит из основания и боковой поверхности. Площадь основания конуса вычисляется по формуле S осн = πr^2, а площадь боковой поверхности конуса — по формуле S бок = πrl, где l — образующая конуса, которая представляет собой линию, соединяющую вершину конуса с точкой основания.
Таким образом, геометрические свойства конуса определяют его форму, структуру и позволяют рассчитывать его объем и поверхность, что делает его полезным в различных задачах и приложениях.
Примеры использования конусов
Конусы используются во многих областях человеческой деятельности. Вот несколько примеров, где мы можем встретить конусы:
1. Архитектура
В архитектуре, конусы часто используются в строительстве монументов и зданий. Например, коническая форма может быть использована для создания куполов, шпилей и башен, придающих зданиям эстетическую привлекательность и уникальность.
2. Промышленность
Конусы широко применяются в промышленности для создания различных товаров и оборудования. Например, конические буртики используются для соединения двух труб разного диаметра, а коническая машинка шлифует и полирует поверхности.
3. Музыкальные инструменты
В некоторых музыкальных инструментах, например, тыбо, певец использует конусообразный рожок, чтобы усилить и направить звук.
4. Упаковка
Конусообразная упаковка может быть использована для упаковки кондитерских изделий, мороженого или других видов пищи. Такая форма обеспечивает стабильность и защиту продуктов.
Это лишь некоторые примеры использования конусов, их применение может быть гораздо шире и разнообразнее в зависимости от конкретной задачи и отрасли.
История изучения конусов

Изучение конусов началось еще в древности. Древние греки и египтяне использовали конусы при строительстве пирамид и других сооружений. Они заметили, что конусы имеют определенные геометрические свойства и могут быть использованы для решения различных задач.
Однако, первые математические изыскания в области конусов были проведены в Древней Греции. Знаменитый греческий математик Пифагор (около 570-495 г. до н. э.) рассмотрел основные свойства конусов и доказал ряд теорем, связанных с ними.
Позднее, во время Античности, Архимед (287-212 г. до н. э.) продолжил исследование конусов и разработал методы для вычисления их объема и площади. Он также предложил принцип, который сейчас известен как принцип Архимеда, и который позволяет определить объем конуса путем образования его поверхности на поверхности цилиндра.
В средние века изучение конусов было связано с развитием альхимии и мистицизма. Многие альхимики видели в конусах символичность и связывали их с магическими и оккультными силами.
С развитием новых математических методов и открытием дифференциального и интегрального исчисления, изучение конусов стало более точным и систематическим. В 17 веке французский математик Блез Паскаль (1623-1662) продолжил работы Архимеда и разработал теорию конических сечений.
С тех пор изучение конусов не прекращалось. Современные математики используют конусы для решения различных задач в геометрии, физике, инженерии и других областях знаний. Конусы также являются предметом изучения в школьной программе по геометрии.
Ссылки на другие геометрические фигуры
| Тело | Описание |
|---|---|
| Сфера | Геометрическое тело, состоящее из всех точек в трехмерном пространстве, находящихся на одном и том же расстоянии от определенной точки. |
| Пирамида | Геометрическое тело, состоящее из многоугольника в форме основания и треугольников, которые сходятся к одной точке, называемой вершиной. |
| Цилиндр | Геометрическое тело, имеющее два одинаковых основания в форме круга, соединенных цилиндрической поверхностью. |
| Параллелепипед | Геометрическое тело, имеющее шесть прямоугольных граней, противоположные которых пары параллельны. |
Каждое из этих тел обладает своими уникальными свойствами и применениями в различных областях. Изучение геометрических фигур помогает улучшить понимание пространства и форм, что является важным в математике и других науках.
Вопрос-ответ:
Что такое конус?
Конус — это геометрическая фигура, которая имеет форму трехмерного объекта и состоит из плоской основы, которая соединена с вершиной специальной кривой линией, называемой боковой поверхностью.
Как выглядит конус?
Конус выглядит как трехмерная фигура, похожая на треугольную пирамиду, но с круглой или овальной основой.
Как определить высоту конуса?
Чтобы определить высоту конуса, нужно провести линию от вершины конуса до центра его основы. Эта линия будет являться высотой конуса.
Где применяются конусы в реальной жизни?
Конусы применяются в различных сферах нашей жизни. Например, конусы используются как форма для изготовления мороженого, конусовидные предметы встречаются в архитектуре, а также конусы применяются при строительстве и в множестве других областей.