Квадрат числа – это результат возведения числа в квадрат. Математически это означает, что квадрат числа равен произведению этого числа на себя. Например, квадрат числа 5 равен 25, так как 5 * 5 = 25. Здесь число 5 называется основанием квадрата. Квадрат числа является одной из основных операций в алгебре и имеет широкий спектр применения в различных областях.
Понятие квадрата числа возникло еще в древности и имеет глубокие корни в геометрии. В геометрическом понимании квадрат числа представляет собой площадь квадрата со стороной, равной этому числу. Например, квадрат числа 5 имеет площадь 25 квадратных единиц. Именно поэтому такое обозначение «возведение в квадрат» – это аналогия с геометрическим понятием площади квадрата.
Квадрат числа имеет ряд интересных свойств. Например, квадрат любого натурального числа всегда больше нуля, так как произведение двух положительных чисел всегда положительно. Кроме того, квадрат числа может быть использован для нахождения площади различных фигур, таких как квадрат, прямоугольник или круг.
Что такое квадрат числа

Число, возводимое в квадрат, называется квадратом этого числа. Квадрат числа получается путем умножения числа на само себя. Например, квадрат числа 3 равен 3 умножить на 3, то есть 9.
Квадрат числа обозначается специальным символом — возведение числа в квадрат выглядит как число, пишется вверху строки и слева от числа. Например, число 3 возводится в квадрат и записывается как 3².
Квадраты чисел имеют много свойств и применений в математике. Они используются, например, для расчетов в геометрии и физике, для решения квадратных уравнений, для определения площади квадрата и многих других задач.
Квадрат числа также можно представить геометрически. Если взять квадрат со стороной, равной данному числу, то его площадь будет равна квадрату этого числа.
Некоторые квадраты чисел имеют специальные имена. Например, квадрат числа 2 равен 4 и называется «четыре». Квадрат числа 10 равен 100 и называется «сто». Квадраты этих чисел часто встречаются в повседневной жизни и имеют свою названную значимость.
Определение квадрата числа
Например, квадрат числа 4 равен 4 умножить на 4, то есть 16.
Таким образом, квадрат числа показывает площадь квадрата со стороной равной данному числу.
Найти квадрат числа можно с помощью оператора возведения в степень или с помощью умножения числа на само себя.
Обозначение квадрата числа: a^2 или a2, где a — число.
Квадрат числа может быть положительным или отрицательным, в зависимости от знака исходного числа.
Знание определения квадрата числа помогает в решении различных математических задач и в понимании различных концепций в геометрии и физике.
Свойства квадратов чисел
У квадратов чисел есть ряд интересных свойств:
- Квадрат любого натурального числа является положительным числом.
- Если число является квадратом, то оно всегда будет неотрицательным.
- Квадрат отрицательного числа будет положительным числом.
- Квадраты всех целых чисел являются положительными числами.
- Квадрат числа может быть представлен как сумма нечётного числа последовательных натуральных чисел.
- Сумма квадратов двух чисел равна (a^2 + b^2).
- Разность квадратов двух чисел равна (a^2 — b^2), и может быть разложена как (a + b)(a — b).
Знание и понимание свойств квадратов чисел помогает в решении различных математических задач и нахождении значений в различных областях науки и техники.
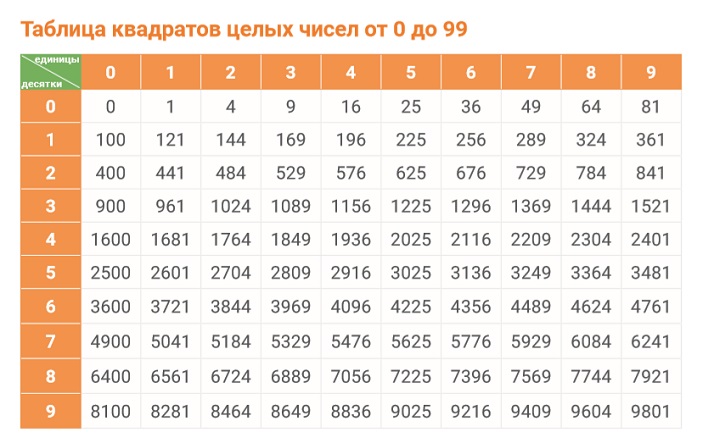
Примеры квадратов чисел

| Число | Квадрат числа |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
Таким образом, квадрат числа можно вычислить, умножив это число на само себя.
Как найти квадрат числа
Квадрат числа можно найти, умножив это число само на себя. Другими словами, чтобы найти квадрат числа, нужно возвести это число во вторую степень.
| Число | Квадрат числа |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| … | … |
И так далее. Число в первом столбце таблицы представляет собой число, для которого мы ищем квадрат, а число во втором столбце представляет собой его квадрат.
Например, для числа 3, квадрат будет равен 9 (3 * 3 = 9). И так далее для всех чисел.
Таким образом, чтобы найти квадрат числа, необходимо умножить это число само на себя.
Отрицательные и десятичные квадраты чисел
Отрицательные квадраты чисел
Отрицательный квадрат числа получается путем умножения числа на само себя и смены его знака. Например, (-3)^2 = 9. Таким образом, -3 * -3 = 9.
Отрицательные квадраты чисел часто встречаются при решении уравнений и в других областях математики. Например, отрицательные квадраты могут использоваться для представления расстояний или скоростей в физических задачах.
Десятичные квадраты чисел
Десятичные квадраты чисел — это результат умножения числа на само себя, когда это число представлено в виде десятичной дроби. Например, 1.5 * 1.5 = 2.25.
Десятичные квадраты чисел также широко используются в науке и инженерии, особенно при работе с физическими величинами, которые могут быть измерены с использованием десятичных дробей, такими как площадь или объем.
Квадрат числа в математических выражениях
Квадрат числа может быть представлен в виде таблицы, где значения исходного числа и его квадрата приведены в разных столбцах:
| Число | Квадрат числа |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
Квадрат числа — важное понятие в алгебре и геометрии. Оно позволяет решать различные задачи, включая определение площади квадрата или построение графиков функций.
Применение квадратов чисел в реальной жизни
Квадраты чисел находят применение во многих аспектах нашей повседневной жизни. Они широко используются в различных областях, таких как физика, математика, геометрия, инженерия и программирование.
Физика и математика
Квадраты чисел помогают нам решать различные физические задачи и моделировать явления в математике. Например, квадрат числа может представлять площадь квадрата или квадрата числового значения в формулах. Рассчитывая площадь или объем объектов, мы используем их квадраты чисел.
Геометрия
В геометрии квадраты чисел используются для измерения и моделирования различных фигур и форм. Квадрат числа является основой для вычисления площади квадрата или прямоугольника. Он также используется для измерения расстояния от точки до точки, а также для определения гипотенузы в треугольниках.
Квадраты чисел также используются для построения графиков и решения систем уравнений в геометрии, что позволяет нам более точно представить и анализировать различные пространственные отношения.
Инженерия и программирование
В инженерии и программировании, квадраты чисел используются для решения различных задач и оптимизации процессов. Например, в алгоритмах машинного обучения, квадраты чисел могут использоваться для измерения различных ошибок и оценки точности моделей.
Также в электротехнике, квадраты чисел могут использоваться для определения мощности или напряжения в электрических цепях.
В общем, квадраты чисел играют важную роль в реальной жизни, помогая нам измерять, моделировать и анализировать различные явления и процессы в различных областях знаний.
Вопрос-ответ:
Что такое квадрат числа?
Квадрат числа — это результат умножения числа на себя. Например, квадрат числа 4 равен 16, так как 4 умножено на 4.
Как найти квадрат числа?
Чтобы найти квадрат числа, нужно умножить это число само на себя. Например, чтобы найти квадрат числа 5, нужно умножить 5 на 5, что дает результат 25.
Зачем нужны квадраты чисел?
Квадраты чисел используются в математике и других научных областях. Они позволяют решать различные задачи, вычислять площади и объемы, а также анализировать данные. Квадраты чисел также применяются в квадратных уравнениях и геометрии.
Как связаны квадраты чисел и квадратные корни?
Квадрат числа и квадратный корень числа являются обратными операциями. Например, квадратный корень из 16 равен 4, так как 4 умноженное на себя даст 16. И наоборот, квадрат числа 4 равен 16.