Какой угол называется линейным углом двугранного угла

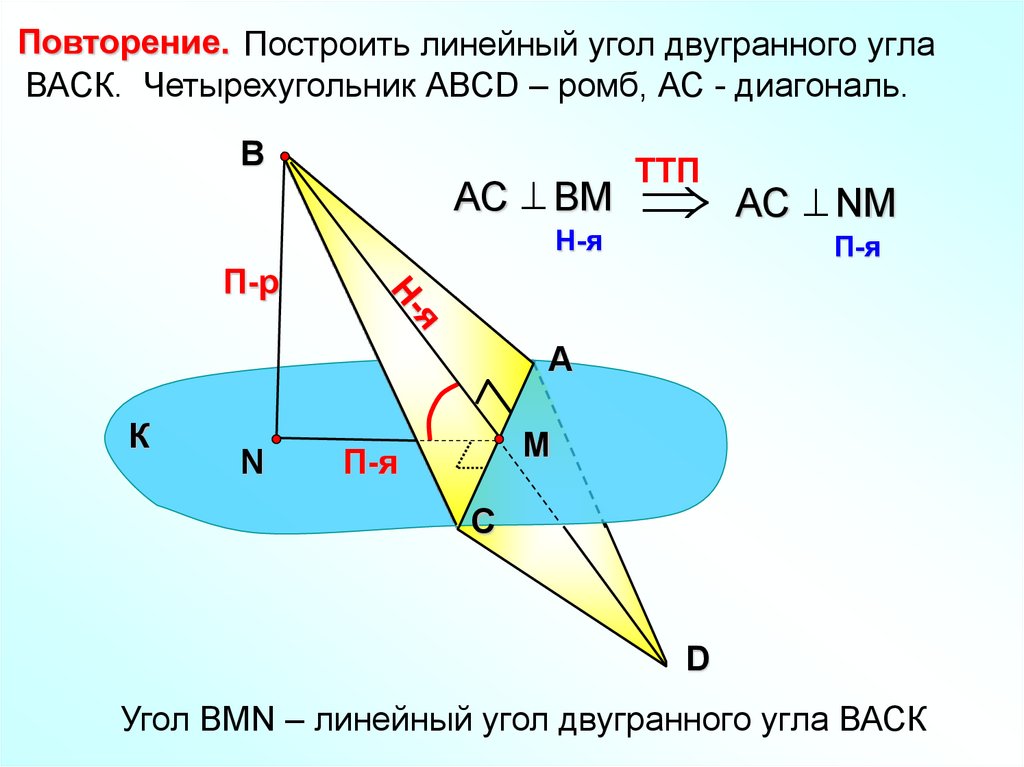
Для того чтобы разобраться в терминах и определениях геометрии, нам необходимо углубиться в изучение двугранных углов. Однако перед тем, как мы перейдем к этому понятию, необходимо понять, что такое линейный угол двугранного угла.

Линейный угол представляет собой угол, образованный двумя смежными прямыми линиями и ограниченный другой прямой, называемой пересекающей. Он имеет следующую особенность: сумма линейных углов, образованных пересекающей прямой и двумя смежными прямыми, равна 180 градусам. Именно поэтому ему и называют линейным — это угол, прямая часть которого незамкнута.

Активно используется понятие линейного угла двугранного угла в различных дисциплинах, связанных с геометрией, а также в практических задачах, связанных с расчетами и измерением углов. Оно является одним из основных элементов теории углов и позволяет нам более точно определить расположение и направление линий и плоскостей в пространстве.

Содержание

Понятие двугранного угла

Свойства двугранного угла:

Двугранный угол имеет общую вершину, где начинаются его две стороны.
Стороны двугранного угла являются продолжением сторон линейных углов.
Два линейных угла, образующих двугранный угол, могут быть разнонаправленными (внутренний) или смотреть в противоположные стороны (внешний).
Сумма мер линейных углов, образующих двугранный угол, равняется 180 градусам.

Линейный угол, который составляет одну из сторон двугранного угла, называется внутренним углом, а линейный угол, который лежит по другую сторону от вершины двугранного угла, называется внешним углом. Эти два угла образуют пару, которая вместе составляет двугранный угол.

Определение линейного угла

Линейный угол может быть измерен в градусах или радианах. В градусной мере линейный угол может составлять от 0° до 180°. В радианной мере линейный угол может быть в пределах от 0 до π (пи) радиан.

Линейный угол является частью двугранного угла, который образуется двумя противолежащими (непересекающимися) линейными углами, имеющими общую вершину. Каждый из этих линейных углов называется половинным линейным углом. Их сумма равна исходному двугранному углу.

Линейные углы играют важную роль в геометрии и используются для измерения поворотов и направлений объектов. Они широко применяются в различных областях, включая строительство, навигацию, машиностроение и графическое моделирование.

Как образуется линейный угол двугранного угла

Для того чтобы определить линейный угол двугранного угла, необходимо провести прямую линию от точки пересечения двух плоскостей до любой точки на грани, не принадлежащей этой прямой линии.

Определение

Линейный угол двугранного угла образуется двумя прямыми линиями, которые лежат в разных плоскостях и пересекаются в одной точке. Эти линии называются гранями двугранного угла, а точка пересечения — вершиной двугранного угла.

Свойства

Линейный угол двугранного угла всегда равен 180 градусов или π радиан. Величина линейного угла может быть измерена с помощью градусного или радианного измерения.

Линейный угол двугранного угла может быть выпуклым или вогнутым. Если грани двугранного угла образуют выпуклый угол, то линейный угол также будет выпуклым. В случае, когда грани образуют вогнутый угол, линейный угол будет вогнутым.

Линейный угол двугранного угла может быть полным или неполным. Полный линейный угол равен 180 градусов или π радиан, тогда как неполный линейный угол имеет значение меньше 180 градусов или π радиан.

Важно: Линейный угол двугранного угла влияет на форму и структуру самого двугранного угла. Для того чтобы точно определить двугранный угол, необходимо знать его линейный угол.

Характеристики линейного угла

Основные характеристики линейного угла:

Величина линейного угла измеряется в градусах и обычно обозначается символом °.
Сумма всех углов вокруг точки равна 360°. Таким образом, сумма всех линейных углов в двугранном угле также равна 360°.
Линейный угол может быть выпуклым, когда две прямые линии расположены с одной стороны от вершины, или вогнутым, когда они расположены с обоих сторон.
Если две прямые линии параллельны, то линейный угол между ними равен 180°.

Линейные углы широко используются в геометрии и физике для измерения и анализа угловых отношений. Они помогают понять структуру и связи между прямыми линиями и плоскостями.

Свойства линейного угла

Основные свойства линейного угла:

1. Сумма углов линейного угла равна 180 градусов.

Следующее свойство линейного угла основано на свойстве парных углов, которые образуются при пересечении двух прямых.

2. Парные углы, образованные взаимно перпендикулярными линиями, являются равными.

Из этих свойств линейного угла следует, что если сумма двух углов линейного угла равна 180 градусов, то каждый угол этого линейного угла также равен 180 градусов.

Важно отметить, что в контексте двугранного угла линейный угол может иметь другую степень, не равную 180 градусов, в зависимости от его положения относительно другого угла двугранного угла.

Виды линейных углов

1. Внутренний линейный угол

Внутренний линейный угол — это угол, который расположен внутри двугранного угла и образуется внутри него. Он представляет собой разделение двугранного угла на две половины.

Примером внутреннего линейного угла может служить угол между сторонами книги, ограничивающим прямой угол, или угол между боковинами стола, ограничивающим острые углы.

2. Внешний линейный угол

$2. Внешний линейный угол$

Внешний линейный угол — это угол, который расположен снаружи двугранного угла и образуется продолжением его сторон. Он представляет собой разделение прямой линии вне двугранного угла.

Примером внешнего линейного угла может служить угол между сторонами окна или угол между сторонами стены.

Понимание этих двух видов линейных углов поможет вам более глубоко изучить двугранные углы и использовать их в решении задач и проблем, где они встречаются.

Примеры использования линейных углов

Пример	Описание
Строительство	В строительстве линейные углы используются для определения наклона и направления строительных конструкций. Например, при проектировании крыши здания необходимо учесть угол наклона, чтобы обеспечить правильное стекание дождевой воды. Линейные углы также используются для определения угла наклона горных склонов при строительстве дорог и трасс.
Разметка дорог	При разметке дорог линейные углы используются для определения направления движения транспортных средств. Дорожные знаки, пешеходные переходы и разметка полос движения устанавливаются с определенным углом, чтобы обеспечить безопасность и эффективность дорожного движения.
Архитектура	В архитектуре линейные углы используются для определения формы и пропорций зданий. При проектировании фасадов и интерьеров зданий архитекторы учитывают углы, чтобы достичь желаемого эстетического и функционального результата.
Изготовление мебели	При изготовлении мебели линейные углы используются для обеспечения правильной сборки и крепления деталей. Кроме того, линейные углы помогают достичь симметричности и гармонии в дизайне мебели.

Это лишь некоторые примеры использования линейных углов. В геометрии и других областях науки и техники углы являются важным инструментом для измерения и понимания пространства. Понимание линейных углов помогает нам строить и проектировать различные объекты и структуры, обеспечивать их эффективность, безопасность и эстетику.