Ломаная — это геометрическая фигура, состоящая из прямых отрезков, соединенных в точках, называемых вершинами. Эти отрезки могут быть различной длины и образовывать разнообразные формы. Ломаная является одной из основных фигур в геометрии и широко применяется в разных областях, таких как архитектура, дизайн и даже в программировании.
Каждая ломаная задается своими звеньями, вершинами и длинами. Звеньями называются отрезки, соединяющие соседние вершины, а вершинами — точки пересечения этих отрезков. Длина каждого отрезка определяет форму и геометрические свойства ломаной. Чем больше длины отрезков, тем более сложной и плавной будет форма фигуры.
Ломаная может иметь произвольное количество звеньев и вершин. Также она может быть замкнутой (когда последняя вершина соединена с первой) или открытой (когда концы ломаной не соединены). Форма ломаной может быть правильной или неправильной, симметричной или асимметричной. Комбинируя различные звенья и вершины, можно создавать самые разнообразные формы и контуры.
Использование ломаных в геометрии позволяет наглядно представлять различные объекты и фигуры. Они широко применяются для построения графиков, диаграмм, карт и других визуальных представлений данных. Также ломаные могут использоваться для моделирования сложных изгибов и линий в дизайне и архитектуре, при создании компьютерной графики и трехмерных моделей. Понимание основных свойств ломаных поможет в создании и анализе сложных геометрических форм и фигур.
Определение ломаной
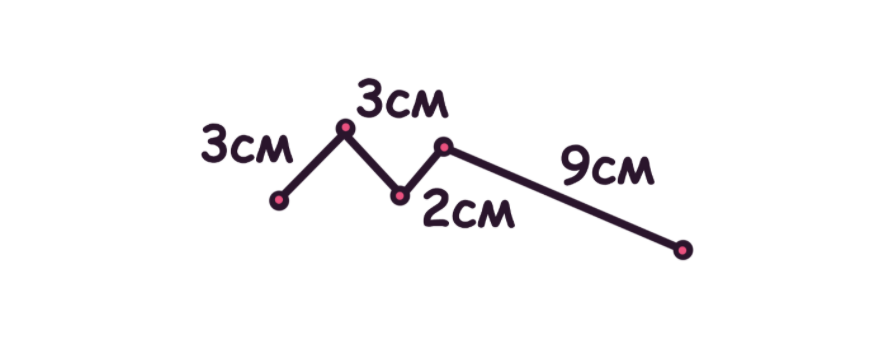
На рисунке ниже показан пример ломаной с тремя звеньями:
| –– | –– | –– |
В данном случае ломаная имеет три звена и четыре вершины. Длина ломаной равна сумме длин всех ее звеньев. Определение ломаной может быть использовано в различных областях, таких как графика, компьютерное моделирование, картография и дизайн.
Ломаная как геометрическая фигура
Для определения ломаной необходимо знать координаты ее вершин. Вершины ломаной обозначаются буквами латинского алфавита, например, A, B, C, и т.д. Для каждой вершины указывается ее координата в виде упорядоченной пары чисел (x, y), где x — это абсцисса (горизонтальная координата), а y — это ордината (вертикальная координата).
Важным свойством ломаной является ее длина. Длина ломаной определяется суммой длин всех звеньев, то есть расстоянием между каждой парой последовательных вершин. Для вычисления длины ломаной используется формула длины отрезка между двумя точками на плоскости.
| Вершина | Координаты |
|---|---|
| A | (xA, yA) |
| B | (xB, yB) |
| C | (xC, yC) |
Длина ломаной AB равна sqrt((xB — xA)^2 + (yB — yA)^2).
Длина ломаной BC равна sqrt((xC — xB)^2 + (yC — yB)^2).
И так далее для всех последовательных звеньев ломаной.
Знание вершин, звеньев и длины ломаной позволяет анализировать ее свойства и использовать в различных геометрических задачах.
Ломаная как математический объект
Для того чтобы полностью определить ломаную, необходимо знать координаты вершин и длину каждого звена. Вершины ломаной представляются парой чисел (x, y), где x – абсцисса вершины, y – ордината вершины.
Пример: Рассмотрим ломаную с четырьмя вершинами и трех звеньями. Координаты вершин данной ломаной будут следующими: A(0, 0), B(2, 1), C(3, -1), D(5, 0). Длины звеньев: AB = 2, BC = 1, CD = 2. Таким образом, ломаная определена координатами вершин и длинами звеньев.
Ломаные широко используются в различных областях математики, физики и компьютерной графики. Они позволяют описывать сложные фигуры и моделировать различные объекты, такие как траектории движения, геометрические конструкции и многие другие.
Ломаная как графическое представление данных
Ломаная может использоваться для визуализации различных видов данных, таких как временные ряды, тренды, графики изменений и другие. Она позволяет увидеть зависимость между значениями данных и выделить особенности и тренды.
Применение ломаных в анализе данных позволяет выявить взаимосвязи, обнаружить выбросы и аномалии, сравнить различные наборы данных. Они также могут быть использованы в прогнозировании и построении моделей, чтобы предсказать будущее поведение данных.
Ломаные могут быть построены вручную или с использованием специальных программ или инструментов. Они могут быть представлены в двухмерном или трехмерном пространстве. Для построения ломаной необходимо знать значения данных и их порядок, чтобы правильно соединить вершины и отрезки.
В итоге, ломаная представляет собой графическое изображение данных, которое помогает наглядно представить информацию, выявить тренды и закономерности, а также провести анализ и сравнение данных.
Звенья и вершины ломаной
Число звеньев ломаной определяет количество отрезков, из которых она состоит. Число вершин равно числу начал и концов звеньев плюс число точек пересечения или соприкосновения. Длина ломаной – это сумма длин всех ее звеньев.
Знание звеньев и вершин ломаной позволяет анализировать ее форму и структуру. Например, если ломаная имеет много вершин и сложный паттерн звеньев, она может быть более изогнутой и нерегулярной. С другой стороны, если ломаная имеет мало вершин и простой паттерн звеньев, она может быть более прямой и регулярной.
Звенья и вершины ломаной играют важную роль в различных областях, таких как графика, компьютерное моделирование и картография. Они позволяют представлять и анализировать сложные формы и структуры в удобной форме, облегчая работу с геометрическими объектами.
Значение звеньев в геометрии
Длина звена влияет на периметр и площадь фигуры. Чем больше длина звена, тем больше площадь фигуры, образованной ею. Также длина звена может влиять на пропорции фигуры и ее внешний вид. Например, в случае ломаной, состоящей из звеньев различной длины, каждое звено будет вносить свой вклад в формирование формы фигуры.
Кроме того, звенья могут быть использованы для определения углов фигуры. Если знать длины звеньев и положение вершин, можно вычислить углы треугольника или другой многоугольной фигуры, образованной звеньями. Звенья могут быть использованы для определения и исследования различных свойств геометрических фигур, таких как симметрия или правильность.
Таким образом, значение звеньев в геометрии заключается в их роли в определении формы, размеров и свойств фигуры. Знание длин звеньев позволяет проводить различные геометрические вычисления и анализировать характеристики фигур.
Вершины ломаной и их роль
Каждая вершина ломаной имеет координаты, которые определяют ее положение на плоскости. Зная координаты вершин, можно определить длину каждого звена ломаной, а также ее общую длину. Координаты вершин часто задаются в виде пар чисел (x, y) или (x, y, z), где x, y, z — значения по осям x, y, z соответственно.
Вершины ломаной также могут быть помечены числами, буквами или другими символами для обозначения порядка следования. Нумерация вершин обычно начинается с 1 или 0 и продолжается последовательно до конца ломаной. Отметки вершин упрощают работу с ломаной, позволяют легко определить порядок и связь между вершинами.
Роль вершин ломаной состоит в определении ее формы, направления и углов между звеньями. Изменение положения вершин может привести к изменению формы ломаной, ее длины и других свойств. Кроме того, вершины могут использоваться для определения вида ломаной (отрезки, кривая, полигон) и ее границ.
Вершины ломаной являются ключевыми элементами при работе с геометрическими исчислениями, моделированием, а также при решении практических задач, связанных с измерениями, трассировкой линий и маршрутами движения.
Взаимосвязь звеньев и вершин ломаной
Количество звеньев и вершин в ломаной зависит от ее сложности и конструктивных особенностей. Чем больше вершин, тем более детализированная и изогнутая форма у ломаной.
Звенья ломаной являются отрезками прямых линий, соединяющими смежные вершины. Длина каждого звена определяется расстоянием между соответствующими вершинами. Сумма длин всех звеньев ломаной равна ее периметру.
Вершины ломаной являются конечными точками звеньев, где они соединяются. Каждая вершина имеет свои координаты, определяющие ее положение в пространстве. Совокупность координат вершин задает форму и размеры ломаной.
Связь между звеньями и вершинами ломаной является взаимной: звенья определяют положение вершин, а вершины определяют форму и длину звеньев. Изменение положения или количества звеньев и вершин приводит к изменению формы и размеров ломаной.
Таким образом, для полного определения ломаной необходимо знать количество звеньев, координаты вершин и длину каждого звена. Все эти параметры тесно связаны между собой и определяют геометрические свойства ломаной.
Вопрос-ответ:
Что такое ломаная определение фигуры ее звеньев вершин и длины?
Ломаная — это геометрическая фигура, составленная из отрезков, называемых звеньями. Звенья образуют вершины, где они соединяются. Длина ломаной определяется суммой длин всех звеньев, которые ее составляют.
Каким образом можно определить длину ломаной фигуры?
Длину ломаной фигуры можно определить путем сложения длин всех звеньев, из которых она состоит. Для этого необходимо знать длины каждого звена и просуммировать их значения. Итогом будет общая длина ломаной.
Можете ли вы объяснить, как строится ломаная фигура?
Ломаная фигура строится путем соединения отрезков, называемых звеньями. При построении ломаной каждый отрезок начинается с конца предыдущего звена и соединяется с началом следующего звена. В результате получается ломаная линия, образующая вершины соединения звеньев.
Чем отличается ломаная фигура от других геометрических фигур?
Ломаная фигура отличается от других геометрических фигур, таких как прямоугольник, треугольник или круг, тем, что она состоит из отрезков, связанных вершинами. Другие геометрические фигуры могут иметь определенные углы и форму, в то время как у ломаной фигуры форма не обязательна и может быть произвольной.