
В математике неравенства играют важную роль, позволяя нам сравнивать значения переменных. Неравенство называется верным, если оно выполняется для определенного значения переменной. Но как найти это значение?
Перед решением неравенств нужно понять, какие операторы используются. Самые распространенные операторы в неравенствах — «больше» (>) и «меньше» (<). Например, неравенство 2x - 5 > 10 говорит нам, что двойное значение переменной, уменьшенное на 5, больше 10.
Для нахождения значения переменной при котором неравенство выполняется, нужно следовать нескольким правилам. Во-первых, при переносе чисел или переменных из одной части неравенства в другую нужно изменить их знак на противоположный. Например, если у нас есть неравенство 2x — 5 > 10, при переносе в другую часть неравенства -5 станет +5 и мы получим, что 2x > 15.
Далее, нужно разделить обе части неравенства на коэффициент при переменной, чтобы избавиться от него. В нашем примере коэффициент при x равен 2, поэтому результатом будет x > 7,5. И это уже значение переменной, при котором неравенство 2x — 5 > 10 станет верным.
Определение неравенства и его значения
Значение переменной в неравенстве – это число или диапазон чисел, для которых данное неравенство становится истинным.
Чтобы определить значение переменной в неравенстве, необходимо решить неравенство и найти множества значений, при которых оно выполняется.
Например, рассмотрим неравенство 2x + 3 > 7. Чтобы найти значение переменной x, необходимо решить это неравенство:
- Вычитаем 3 из обеих частей неравенства:
2x > 4. - Делим обе части неравенства на 2:
x > 2.
Таким образом, значение переменной x в данном неравенстве – любое число, большее 2.
Значение переменной в неравенстве может быть единственным числом, диапазоном чисел или совокупностью условий, удовлетворяющих данному неравенству.
Нахождение и интерпретация значения переменной в неравенстве является важной задачей в математике и ее приложениях, таких как физика, экономика, графическая интерпретация данных и многое другое.
Что такое значение переменной в неравенстве?
Неравенства — это математические выражения, содержащие знаки «>,»<",">=» или «<=". Значение переменной в неравенстве может быть конкретным числом, или диапазоном чисел, или зависеть от других переменных.
Пример 1:
Рассмотрим неравенство 2x — 3 < 7. Чтобы неравенство было истинным, значение переменной x должно быть меньше 5, потому что:
2 * 5 — 3 = 10 — 3 = 7, что уже не меньше 7.
Пример 2:
Пусть дано неравенство x^2 > 9. Чтобы неравенство было истинным, значение переменной x должно быть больше -3 или меньше -3, потому что:
При x = -3, (-3)^2 = 9, что уже не больше 9.
Значение переменной в неравенстве может быть определено аналитически или графически с использованием интуитивного понимания математических операций.
Поиск значения переменной в неравенстве может быть полезен при решении математических задач, построении графиков функций, определении интервалов, на которых выполняются определенные условия и многих других ситуациях.
Понятие истинности неравенства
Истинность неравенства определяется значением переменной, при котором неравенство становится верным или ложным. Если при некотором значении переменной неравенство выполняется, оно считается истинным, а если оно не выполняется, оно является ложным.
Важно отметить, что истинность неравенства зависит от допустимого диапазона значений переменной. Например, неравенство «x > 5» будет истинным, если переменная x принимает значения больше 5.
Примеры истинности неравенств:
1. Дано неравенство «2x + 3 < 9". Если рассмотреть значение x = 2, то получим "2 * 2 + 3 < 9", что эквивалентно "7 < 9". Так как это неравенство выполняется, оно является истинным.
2. Дано неравенство «4y — 5 > 20». При x = 10 получим «4 * 10 — 5 > 20», что эквивалентно «35 > 20». Так как это неравенство выполняется, оно является истинным.
Примеры ложности неравенств:
1. Дано неравенство «3a + 8 < 15". Если рассмотреть значение a = 3, то получим "3 * 3 + 8 < 15", что эквивалентно "17 < 15". Так как это неравенство не выполняется, оно является ложным.
2. Дано неравенство «2b — 9 > 50». При x = 20 получим «2 * 20 — 9 > 50», что эквивалентно «31 > 50». Так как это неравенство не выполняется, оно является ложным.
Когда неравенство обращается в верное?
Неравенсть может быть обращена в верное, когда значение переменной удовлетворяет условию неравенства. Для этого необходимо проверить все возможные значения переменной и найти те, для которых неравенство становится истинным утверждением.
Существует несколько способов определения значений переменной, при которых неравенство обращается в верное. Один из таких способов — графический метод, который позволяет наглядно представить все точки на числовой оси, удовлетворяющие условию неравенства. Другим способом является алгебраический метод, при котором используются математические операции и свойства неравенства для определения допустимого диапазона значений переменной.
Примеры:
1. Рассмотрим неравенство x + 5 < 10. Для того, чтобы неравенство обратилось в верное, необходимо, чтобы значение переменной x было меньше 5.
2. Пусть дано неравенство 2x — 3 > 7. Чтобы неравенство обратилось в верное, значение переменной x должно быть больше 5.
Таким образом, значения переменной, при которых неравенство обращается в верное, могут быть определены с помощью различных методов и зависят от условия неравенства.
Примеры неравенств с их значениями
Ниже представлены примеры неравенств с их значениями:
Пример 1:
- Неравенство: x < 5
- Значение переменной: x = 3
При значении переменной x = 3, неравенство x < 5 истинно, так как 3 меньше 5.
Пример 2:
- Неравенство: y > -2
- Значение переменной: y = 0
При значении переменной y = 0, неравенство y > -2 истинно, так как 0 больше, чем -2.
Пример 3:
- Неравенство: z + 7 ≤ 12
- Значение переменной: z = 5
При значении переменной z = 5, неравенство z + 7 ≤ 12 истинно, так как 5 + 7 = 12, что меньше или равно 12.
Значение переменной в неравенстве: практические примеры
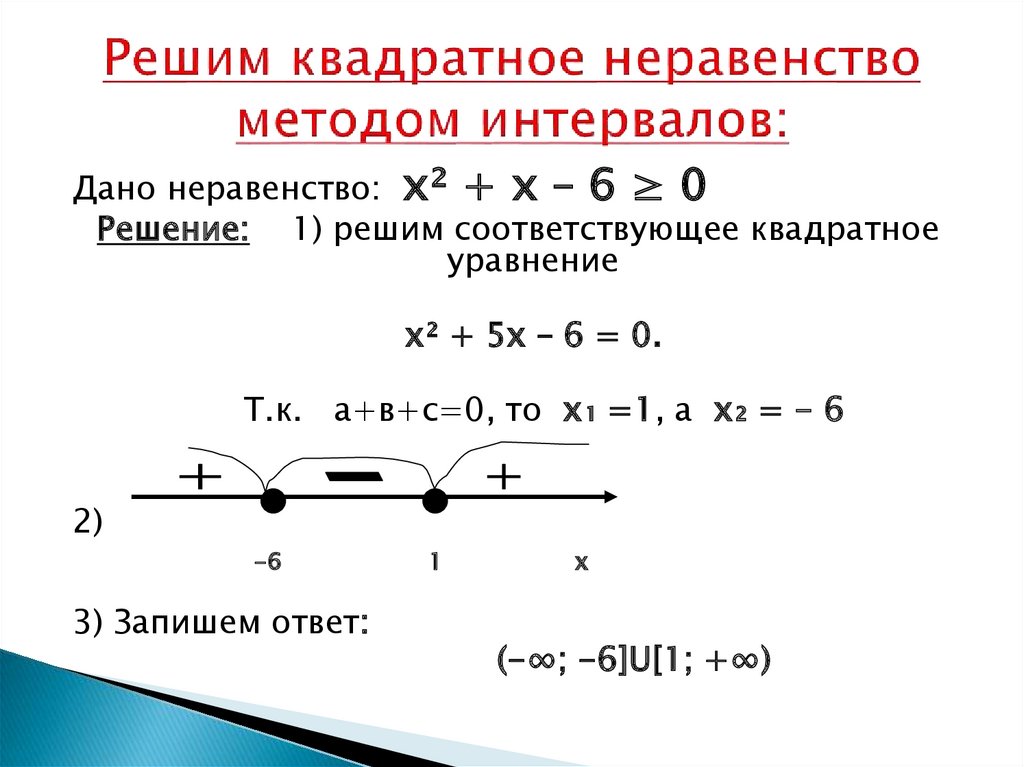
Значение переменной в неравенстве играет важную роль в математике и позволяет найти значения, при которых неравенство выполняется истинно. Практические примеры помогут лучше понять этот концепт и применить его в реальных задачах.
Рассмотрим пример неравенства: x + 3 > 7. Чтобы найти значение переменной x, при котором неравенство будет истинно, мы должны выполнить следующие шаги:
- Вычесть 3 из обеих сторон неравенства: x > 7 — 3.
- Упростить: x > 4.
Таким образом, значение переменной x должно быть больше 4, чтобы неравенство x + 3 > 7 было верным.
Рассмотрим еще один пример. Пусть у нас есть неравенство: 2x — 5 ≤ 9. Чтобы найти значение переменной x, при котором неравенство будет истинно, мы должны выполнить следующие шаги:
- Добавить 5 к обеим сторонам неравенства: 2x ≤ 9 + 5.
- Упростить: 2x ≤ 14.
- Разделить обе стороны неравенства на 2 (так как перед переменной стоит коэффициент 2): x ≤ 14 ÷ 2.
- Упростить: x ≤ 7.
Таким образом, значение переменной x должно быть меньше или равно 7, чтобы неравенство 2x -5 ≤ 9 было верным.
Это лишь два примера, но концепция значения переменной в неравенстве применяется ко многим другим математическим уравнениям и неравенствам. Практическое применение данного концепта широко распространено в физике, экономике, статистике и других научных областях. Знание и умение использовать это понятие поможет в решении различных задач и построении математических моделей реальных явлений.
Варьирующиеся значения и влияние на истинность
Рассмотрим пример неравенства:
- 2x + 5 > 10
В данном неравенстве переменная x принимает различные значения. В случае если x = 3, неравенство принимает вид:
- 2 * 3 + 5 > 10
- 6 + 5 > 10
- 11 > 10
Таким образом, при x = 3 неравенство истинно.
Однако, если x = 2, неравенство примет вид:
- 2 * 2 + 5 > 10
- 4 + 5 > 10
- 9 > 10
Теперь неравенство является ложным при x = 2.
Таким образом, значение переменной x определяет истинность или ложность неравенства. В зависимости от варьирующихся значений можно определить, при каких значениях неравенство является верным или ложным.
Вопрос-ответ:
Что такое неравенство?
Неравенство — это математическое выражение, в котором два числа сравниваются по величине. Оно может содержать такие знаки сравнения, как «<", ">«, «<=" и ">=». Неравенство определяет отношение между числами и может быть истинным или ложным в зависимости от значений переменных.
Что означает значение переменной при котором неравенство становится истинным?
Значение переменной при котором неравенство становится истинным называется корнем неравенства. Это такое значение переменной, при котором неравенство выполняется и неравенство становится верным высказыванием.
Можно ли решить неравенство без нахождения корней?
Да, в некоторых случаях неравенство можно решить без нахождения корней. Например, если неравенство имеет строгий знак («<" или ">«) и все операции с переменными определены и не изменяют знак в процессе упрощения, то можно сразу сделать вывод о значении переменной, при котором неравенство выполняется.
Что делать, если неравенство содержит неизвестную переменную?
Если неравенство содержит неизвестную переменную, то его нужно решить, то есть найти значения этой переменной, при которых неравенство выполняется. Для этого можно использовать различные методы, например, алгебраические преобразования, использование графиков или численные методы.