Ортонормированный базис – это одно из ключевых понятий, широко применяемых в линейной алгебре, математическом анализе и других областях. Базис – это набор векторов, позволяющий представить любой вектор пространства как линейную комбинацию этих векторов. Ортонормированный базис обладает особыми свойствами, которые делают его особенно полезным и удобным для работы.
Ортонормированность базиса означает, что все его векторы являются ортогональными между собой и имеют единичную длину. То есть, все векторы базиса ортогональны друг другу и отличаются только своей длиной, которая равна единице. Это позволяет использовать ортонормированный базис для удобного и эффективного представления векторов и выполнения различных операций над ними.
Ортонормированный базис имеет множество применений в науке и технике. Он часто используется при работе с матрицами, решении линейных уравнений, построении графиков и моделировании объектов в трехмерном пространстве. Отличительной чертой ортонормированного базиса является его удобство в использовании и интуитивное понимание: каждый вектор базиса можно легко представить себе как направление в пространстве и его длину. Это позволяет более просто и наглядно визуализировать сложные математические объекты и облегчает их анализ.
Ортонормированный базис — что это?
Ортонормированный базис является важным инструментом в линейной алгебре и математическом анализе, так как позволяет упростить многие вычисления и решение задач. Он широко используется в различных областях науки, включая физику, инженерию, статистику, компьютерную графику и другие.
Свойства ортонормированного базиса:
- Все векторы базиса перпендикулярны друг другу.
- Длина каждого вектора равна 1.
- Любой вектор в линейном пространстве может быть представлен как линейная комбинация векторов ортонормированного базиса.
- Ортонормированный базис является ортогональным базисом, но не наоборот.
Примеры ортонормированных базисов:
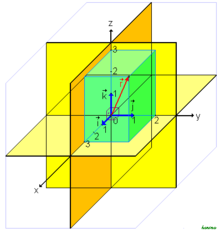
- В трехмерном пространстве единичные векторы вдоль осей координат: (1, 0, 0), (0, 1, 0), (0, 0, 1).
- Тригонометрический базис в пространстве функций: {sin(x), cos(x)}.
- Базис Чебышёва в пространстве полиномов: {1, T₁(x), T₂(x), …, Tₙ(x), …}.
Ортонормированный базис является мощным инструментом, который позволяет решать множество сложных задач в математике и ее приложениях. Изучение ортонормированных базисов является важной частью образования в области математики и науки.
Базис в линейном пространстве
Ортонормированный базис – это специальный вид базиса, в котором все векторы не только линейно независимы, но и ортогональны друг другу и имеют единичную длину. Такой базис позволяет упростить вычисления и имеет множество применений в физике, математике и других науках.
Для проверки ортонормированности базиса можно использовать скалярное произведение. Если все скалярные произведения между векторами равны нулю, а длина каждого вектора равна единице, то базис будет ортонормированным.
Ортонормированные базисы находят применение при решении различных задач, таких как решение систем линейных уравнений, нахождение собственных векторов и собственных значений, а также при описании геометрических объектов в трехмерном пространстве.
Таким образом, ортонормированный базис является важным инструментом в линейной алгебре, который позволяет упростить решение множества задач и облегчить понимание линейных пространств и их свойств.
Ортогональность базисных векторов
1. u и v ортогональны: их скалярное произведение равно нулю: (у, v) = 0;
2. u и v имеют единичную длину: ||u|| = 1 и ||v|| = 1.
Ортогональность базисных векторов важна, так как она позволяет нам более эффективно работать с векторами в пространстве. При наличии ортонормированного базиса мы можем легко находить проекции векторов, вычислять скалярные произведения и решать многие математические задачи.
Ортогональные базисные векторы часто встречаются в математических и физических приложениях, например, в теории сигналов, анализе данных, компьютерной графике и многочисленных других областях. Они являются важным инструментом для описания и изучения различных структур и феноменов в науке и технике.
Нормированность базисных векторов
Нормированные базисные векторы позволяют легко вычислять координаты векторов относительно данного базиса. Для этого достаточно лишь проектировать вектор на каждый базисный вектор и измерять длины этих проекций.
Кроме того, нормированные базисные векторы упрощают обращение матриц и транспонирование матрицы. В особенности, они позволяют получать обратную матрицу путем транспонирования матрицы их координат.
Обычно нормированный базис выбирается таким образом, чтобы его векторы обладали дополнительным свойством ортогональности. Это позволяет выполнить дополнительные упрощения при работе с матрицами и векторами.
Важно отметить, что нормированный базис является одним из важных инструментов в линейной алгебре, позволяющим упростить вычисления и решение различных задач.
Ортонормированный базис
Ортонормированный базис состоит из набора векторов, которые обладают двумя важными свойствами: они ортогональны и нормированы.
Ортогональность
Ортогональность векторов означает, что их скалярное произведение равно нулю. То есть, если имеется два вектора a и b, то их скалярное произведение будет равно 0, если векторы ортогональны: a · b = 0. Это означает, что векторы не имеют общих компонент в направлении друг друга.
Нормированность
Нормированность векторов означает, что их длины равны 1. Длина вектора называется его нормой или модулем и обозначается как ||a||. Имея нормированный базис, можно сказать, что каждый вектор в базисе имеет длину 1 и может быть представлен как единичный вектор.
Ортонормированный базис является удобным инструментом при решении множества задач в математике, физике и других областях. Он позволяет представлять сложные векторы в виде их компонентов, упрощая вычисления и анализ.
Ортонормированный базис также играет важную роль в теории функций, где функции могут быть представлены в виде разложения по базису. Это позволяет решать дифференциальные уравнения и анализировать поведение функций в пространстве.
Особенности ортонормированного базиса
Основная особенность ортонормированного базиса состоит в том, что все векторы этого базиса являются ортогональными друг другу. Это означает, что скалярное произведение любых двух векторов из ортонормированного базиса равно нулю. Такое свойство позволяет упростить многие вычисления и приводит к более ясному и компактному представлению математических формул и уравнений.
Кроме того, векторы ортонормированного базиса имеют единичную длину, то есть каждый вектор имеет норму, равную 1. Это свойство делает ортонормированный базис удобным для работы с евклидовым пространством и позволяет использовать его в различных приложениях, включая геометрию и физику.
Ортонормированный базис является независимым, то есть его векторы не линейно зависимы. Это позволяет использовать ортонормированный базис для разложения произвольного вектора в линейную комбинацию его базисных векторов. Такое разложение является основой для множества операций, включая решение систем линейных уравнений, нахождение проекций векторов и определение собственных значений и собственных векторов.
Важным свойством ортонормированного базиса является его уникальность. Данный базис определен однозначно, то есть для каждого векторного пространства существует только один ортонормированный базис. Это позволяет использовать особенности ортонормированного базиса для доказательства различных теорем и утверждений в линейной алгебре.
Примеры ортонормированных базисов
1. Евклидова плоскость
В евклидовой плоскости можно выбрать ортонормированный базис, состоящий из двух векторов: (1, 0) и (0, 1).
2. Пространство функций
В пространстве функций на отрезке [a, b] можно построить ортонормированный базис из так называемых тригонометрических функций, например, базис Фурье.
3. Комплексные числа
В комплексных числах можно выбрать ортонормированный базис, состоящий из двух векторов: 1 и i.
Это лишь несколько примеров ортонормированных базисов. В действительности, они используются в широком спектре задач, связанных с линейной алгеброй и функциональным анализом.
Применение ортонормированного базиса
Ортонормированный базис очень полезен и находит применение в разных областях науки и техники. Вот некоторые из них:
- Линейная алгебра: Векторы могут быть представлены в виде линейных комбинаций базисных векторов. Ортонормированный базис позволяет упростить вычисления с векторами и матрицами.
- Сигнальная обработка: Ортонормированный базис используется для анализа и синтеза сигналов. Он позволяет представлять сигналы в виде линейных комбинаций базисных функций, что упрощает их обработку.
- Квантовая механика: Ортонормированный базис используется для представления состояний квантовых систем. Он позволяет описывать состояния системы с помощью векторов, что упрощает расчеты и анализ квантовых явлений.
- Машинное обучение: Ортонормированный базис может быть использован для уменьшения размерности данных и выделения наиболее информативных признаков. Это помогает улучшить производительность модели и снижает риск переобучения.
- Кодирование и сжатие данных: Ортонормированный базис может быть использован для сжатия данных и представления их в более компактной форме. Это позволяет уменьшить объем хранимой и передаваемой информации, сохраняя при этом ее содержание.
Применение ортонормированного базиса позволяет упростить и улучшить множество задач в различных областях знания. Его использование позволяет улучшить точность вычислений, уменьшить объем хранимой информации и повысить эффективность алгоритмов обработки данных. Поэтому становится все более популярным в различных областях науки и техники.
Ортонормированный базис является основой для многих математических и физических теорий, в том числе векторного анализа, квантовой механики и гармонического анализа. Благодаря своим особенностям, ортонормированный базис находит применение в различных областях науки и техники.
Использование ортонормированного базиса позволяет упростить расчеты и решение математических задач, а также облегчает визуализацию и понимание геометрических и физических процессов. Знание и понимание ортонормированного базиса является важным элементом математической подготовки и может быть полезным в различных научных и инженерных областях.
В итоге, ортонормированный базис является инструментом, с помощью которого можно более эффективно и точно описывать и анализировать многие явления и процессы в природе, науке и технике.
Вопрос-ответ:
Что такое ортонормированный базис?
Ортонормированный базис — это набор векторов в линейном пространстве, такой что все векторы являются ортогональными друг другу и имеют единичную длину.
Как определить ортонормированный базис в пространстве?
Для определения ортонормированного базиса необходимо проверить два условия: векторы должны быть ортогональными и иметь единичную длину. Если оба условия выполняются, то базис является ортонормированным.
Какие свойства имеет ортонормированный базис?
Ортонормированный базис обладает рядом полезных свойств. Например, он облегчает вычисления векторных произведений и скалярных произведений, а также позволяет легко находить координаты векторов в новом базисе.
Как применять ортонормированный базис в линейной алгебре?
Ортонормированный базис широко используется в линейной алгебре для упрощения вычислений и решения задач. Например, его можно использовать для нахождения ортогональных проекций векторов, ортогонального дополнения подпространств и ортогонального разложения матриц.
Каким образом строится ортонормированный базис?
Существует несколько методов построения ортонормированного базиса. Один из них — метод Грама-Шмидта, при котором векторы последовательно выбираются из исходного базиса и ортогонализируются с помощью проекций на уже построенные векторы.
Что такое ортонормированный базис?
Ортонормированный базис — это набор векторов в линейном пространстве, удовлетворяющий двум условиям: все векторы набора являются ортонормированными, то есть имеют единичную длину и ортогональны между собой, и любой вектор линейного пространства может быть записан в виде линейной комбинации векторов ортонормированного базиса.