Что называется отрезком соединяющим две любые точки на окружности

Отрезком на окружности называется кратчайшее расстояние между двумя заданными точками на окружности. Рассмотрим окружность с заданным радиусом и центром. Каждая точка на окружности имеет определенные координаты, которые можно использовать для определения длины отрезка, соединяющего эти точки.

Важно отметить, что длина отрезка на окружности не зависит от их местоположения. Пусть даны две точки А и В на окружности. Чтобы определить длину отрезка АВ, нужно рассчитать разницу между углами, образованными отрезками от центра окружности до точек А и В.

Формула для расчета длины отрезка, соединяющего две точки на окружности:

D = R * α

Где:

D — длина отрезка, соединяющего две точки на окружности;

R — радиус окружности;

α — угол между отрезками до точек А и В, измеряется в радианах.

Зная радиус и длину угла, можно точно определить длину отрезка на окружности, соединяющего две любые точки. Эта формула имеет широкое применение в геометрии, строительстве, аэронавтике и других областях науки и техники.

Содержание

Что определяется как отрезок, соединяющий две любые точки на окружности?

Длина хорды может быть различной и зависит от расстояния между двумя выбранными точками на окружности. Важно отметить, что длина хорды прямо пропорциональна углу, под которым она проходит. Таким образом, чем больше угол и соответственно длина хорды, тем дальше от центра окружности находятся две точки, которые она соединяет.

Хорда является важным понятием в геометрии окружности и находит применение в различных математических и инженерных задачах. Например, хорда используется в радиусно-кодовой системе, которая используется в навигации и определении координат точек на поверхности Земли.

Окружность и ее основные понятия

Другие важные понятия, связанные с окружностью:

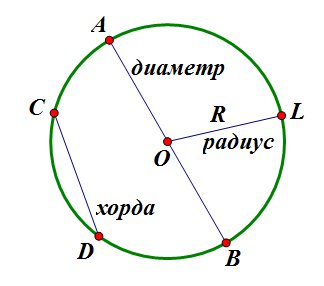
Радиус — отрезок, соединяющий центр окружности с любой точкой на самой окружности. Радиус обозначается символом r и является постоянным для данной окружности.
Диаметр — отрезок, проходящий через центр окружности и ограничивающий ее. Диаметр обозначается символом d и равен удвоенному значению радиуса (d = 2r).
Окружность радиуса 1 — окружность, у которой радиус равен 1.
Длина окружности — периметр окружности, то есть сумма длин всех отрезков, которые можно провести по окружности. Длина окружности вычисляется по формуле L = 2πr, где π (пи) — математическая константа, примерно равная 3.14159.
Отрезок, соединяющий две любые точки на окружности — это отрезок, который можно провести между любыми двумя точками на окружности, не проходя через центр. Данный отрезок называется хордой окружности.

Окружность и указанные важные понятия имеют широкое применение в геометрии, физике, инженерии, а также на практике в строительстве, проектировании и других областях.

Окружность — геометрическая фигура

Вместе с линией, треугольником, прямоугольником и кругом, окружность является фундаментальной фигурой в геометрии. Она имеет множество свойств и применений в математике, физике, инженерии и других науках.

Один из важных элементов окружности — отрезок, соединяющий две любые точки на окружности. Такой отрезок называется хордой. Хорда может быть прямой или кривой и может быть использована для измерения различных параметров окружности, например, длины данной хорды или длины дуги, образованной этой хордой.

Окружность является основой для определения других геометрических фигур, таких как сектор, дуга и сегмент. Она также играет важную роль в тригонометрии, где радиус окружности используется для определения синуса, косинуса и тангенса углов.

В геометрии окружность имеет множество интересных свойств и теорем, которые позволяют изучать и анализировать различные аспекты этой фигуры. Изучение окружности имеет большое практическое значение, особенно в области строительства, где она используется для проектирования круглых зданий, колес и других объектов.

Таким образом, окружность — это геометрическая фигура, которая обладает множеством свойств и применений. Изучение окружности помогает расширить наши знания о геометрии и применить их в различных практических ситуациях.

Точка на окружности — точка пересечения прямой и окружности

Отрезок, соединяющий две любые точки на окружности, называется хордой. Если провести хорду на окружности, она будет пересекать ее в двух точках. Одна из этих точек будет сама хорда, а вторая точка будет точкой пересечения хорды и окружности.

Точка пересечения хорды и окружности может быть как внутри, так и вне окружности. Если точка пересечения лежит внутри окружности, она называется действительной точкой пересечения. Если точка пересечения лежит за пределами окружности, она называется выдуманной точкой пересечения.

Точка на окружности также может быть получена как пересечение прямой и окружности. Прямая и окружность могут пересекаться в двух точках, но только одна из них будет лежать на самой окружности. Эта точка будет точкой на окружности.

Таким образом, точка на окружности является точкой пересечения прямой и окружности и определяется двумя условиями: она находится и на прямой, и на окружности.

Отрезок между точками на окружности — сегмент окружности

Отрезок, соединяющий две любые точки на окружности, называется сегментом окружности. Он представляет собой часть окружности, ограниченную двумя точками и дугой между ними.

Сегмент окружности имеет особые свойства, которые определяют его положение и форму. Длина сегмента зависит от длины дуги и угла, на котором он находится.

Дуга, ограниченная сегментом, может быть меньше, равной или большей половины окружности. При этом, сегмент может быть полным (угол равен 360°), или неполным (угол меньше 360°).

Сегмент окружности может использоваться в геометрических расчетах и задачах. Например, для вычисления площади или периметра фигуры, образованной сегментом окружности, или для определения расстояния между точками на окружности.

Осознание свойств и применение сегментов окружности в геометрии поможет лучше понять различные концепции и задачи, связанные с окружностями и их элементами.

Соединение точек на окружности отрезком

Одним из способов построения отрезка, соединяющего точки на окружности, является использование инструментов геометрии, таких как циркуль и линейка. Можно определить центр окружности и построить окружность с указанными точками в качестве крайних точек. Затем, используя линейку, можно провести прямую линию между этими точками внутри окружности. Получившийся отрезок будет являться отрезком, соединяющим указанные точки на окружности.

Отрезок, соединяющий точки на окружности, имеет важное значение в геометрии и математике. Он используется для определения и изучения различных свойств и теорем, связанных с окружностью. Кроме того, отрезок, соединяющий точки на окружности, может быть использован для построения различных фигур и геометрических конструкций.

Геометрическое понятие отрезка

Отрезком в геометрии называется часть прямой линии, которая соединяет две точки. Понятие отрезка широко используется в различных областях математики, физики, инженерии и других науках.

На окружности отрезком называется часть окружности, которая соединяет две ее любые точки. Любые две точки на окружности можно соединить отрезком, который будет представлять собой дугу окружности. Отрезок на окружности имеет конечную длину и может быть измерен в градусах, радианах или других единицах измерения.

Отрезок соединяющий две точки на окружности называется хордой. Хорда является самым коротким расстоянием между двумя точками на окружности, и она простирается через самый короткий путь на окружности. Хорда также может быть использована для определения дуги, которую она разделяет на окружности. Длина хорды зависит от ее расстояния между точками и радиуса окружности.

Отрезок на окружности является важным геометрическим понятием, используемым в множестве задач и решений. Знание и понимание отрезка на окружности помогает решать задачи связанные с расстояниями и углами на окружности, а также позволяет проводить различные конструкции и получать геометрические доказательства.